§ 6.Приложения интегрального исчисления к решению физических задач

1. Вычисление статических моментов и координат центра тяжести материальной кривой.

а) Пусть материальная точка A массы m отстоит от оси l на расстоянии d. Статистическим моментом этой точки относительно оси l называют число md. Статистическим моментом системы материальных точек расположенных по одну сторону от оси l, массы которых равны , а расстояния от оси l равны , называют число:

= .

Если же эти точки расположены по разные стороны от оси, то для точек, находящихся по одну сторону оси, расстояния берутся положительными, а для точек по другую сторону от оси - отрицательными.

Поэтому если точки расположены на координатной плоскости, = ( ), то = и = ( - статистический момент относительно оси Ox; - относительно оси Oy).

б) Рассмотрим теперь случай, когда масса равномерно распределена по некоторой кривой Г или по некоторой области . Будем считать, что плотность распределения равна единице. Тогда масса дуги численно равна ее длине, а масса области - ее площади.

Начнем со случая кривой линии Г, задаваемой уравнением = , , причем предположим, что функция непрерывна и неотрицательна.

Как обычно, разобьем отрезок на части точками a= ... =b и обозначим через и наименьшее и наибольшее значения функции = на отрезке [ . Этому разбиению соответствует разбиение дуги Г на части (рис. 60).

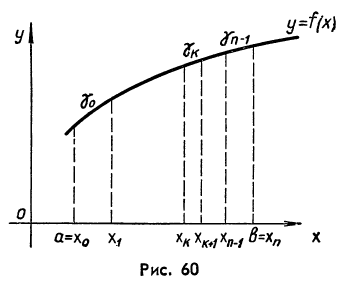
Из физических соображений ясно, что статистический момент части относительно оси абсцисс заключен между и , где - длина этой части, = (напомним, что мы положили линейную плотность дуги равной единице).

Таким образом,:

.

Поэтому:

, т.е.:

.

Так как на отрезке [ ; ] выполняется неравенство: , то в тех же границах, что и , заключен интеграл .

Значит,:

= (1)

Этот интеграл обозначают также следующим образом:

или .

Физики обычно заменяют проведенное рассуждение более коротким. Они берут "бесконечно малый участок дуги" dl. Его статистический момент равен ydl. А статистический момент всей дуги равен сумме элементарных статистических моментов, т.е. . Преимуществом этого вывода является его наглядность. Однако в нем не определено, что такое "бесконечно малый участок дуги", или как еще говорят, "элемент дуги". При уточнении этого понятия мы вновь приходим к более длинному выводу, изложенному ранее. В дальнейшем для краткости изложения будем использовать принятый в физике метод рассуждений. С его помощью сразу выводим, что:

= = . (2)

Как формула (1), так и формула (2) верны и в случае, когда кривая Г пересекает оси координат.

в) Введем понятие центра тяжести.

Определение. Центром тяжести тела называется такая точка С, что если в ней сосредоточить всю его массу, то статический момент этой точки относительно любой оси будет равен статическому моменту всего тела относительно той же оси.

Обозначим через и расстояния центра тяжести кривой от осей ординат и абсцисс.

Тогда, пользуясь определением центра тяжести кривой, получим:

=l = ; = = .

Разрешая полученные равенства относительно и , найдем координаты центра тяжести плоской кривой Г:

= ; = .

Замечание. Если кривая расположена симметрично относительно некоторой прямой, то центр тяжести такой кривой находится на этой прямой.

Это замечание позволяет в некоторых случаях упростить нахождение координат центра тяжести плоской кривой.

Пример 1. Найдем статический момент полуокружности относительно диаметра.

Решение. Выберем систему координат так, чтобы центр окружности совпал с началом координат, а диаметр, относительно которого мы ищем статический момент, совпал с осью Ox. Тогда статический момент полуокружности относительно диаметра выразится формулой:

= , где dl= dx - дифференциал дуги кривой y= .

В выбранной системе координат уравнение полуокружности запишется так:

y= .

Тогда:

y'=- , 1+ =1+ = ,и потому dl= .

Следовательно,:

= =2R =2Rx| =2 .

Пример 2. Найдем центр тяжести четверти окружности + =4, расположенной в первом квадранте.

Решение. Данная кривая расположена симметрично относительно биссектрисы первого координатного угла, следовательно, центр тяжести этой кривой лежит на биссектрисе, а потому = .

Достаточно найти только , пользуясь формулой:

=

Вычисление проще провести, перейдя к параметрическим уравнениям окружности. Так как ее радиус равен двум, то для четверти окружности имеем:

.

Отсюда находим, что:

=-2 , = ,

dl= = =2dt.

Поскольку длина l четверти данной окружности равна = , то:

= = = .