Найти максимальный поток и минимальный разрез в графе, продемонстрировав работу алгоритма Форда-Фалкерсона
Пример. Задана матрица пропускных способностей графа. Найти максимальный поток и минимальный разрез
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
|
5 |
40 |
5 |
|
|
|
|
2 |
|
|
|
|
5 |
|
|
|
3 |
|
30 |
|
30 |
|
20 |
|
|
4 |
|
|
|
|
|
|
5 |
|
5 |
|
|
|
|
|
|
|
15 |
6 |
|
|
|
|
5 |
|
5 |
5 |
7 |
|
|
|
|
|
|
|
15 |
8 |
|
|
|
|
|
|
|
|
Решение
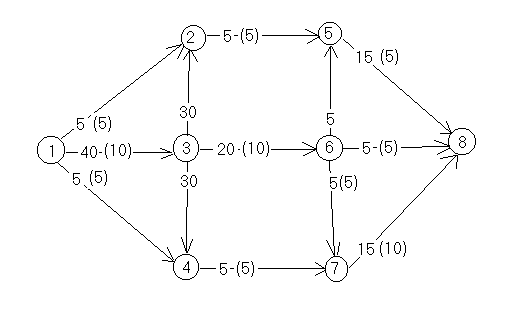
Исходный граф имеет вид. Найдем для него некоторый поток (не обязательно максимальный)
Н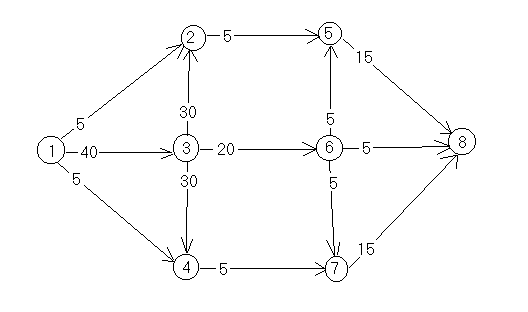
айдем
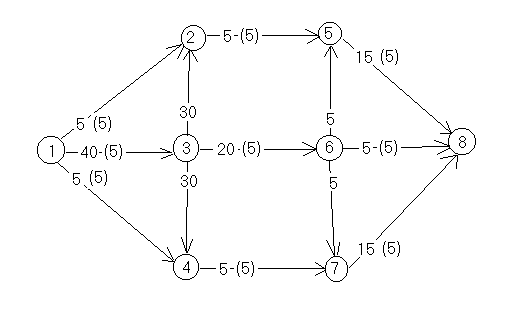
путь, по которому можно увеличить поток
и увеличим поток
Е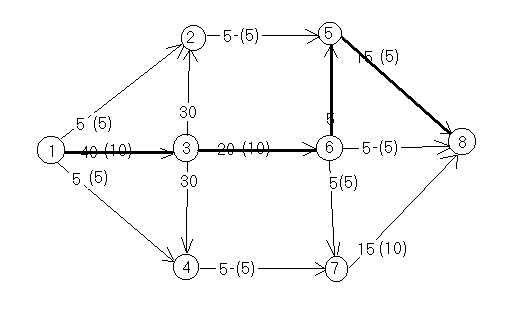
сть
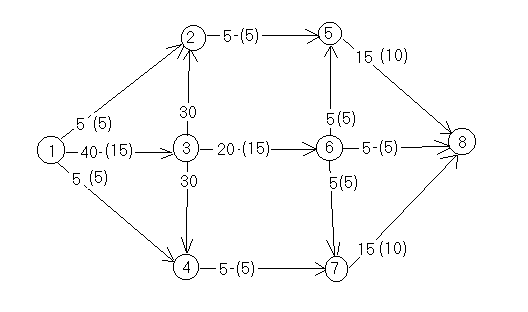
еще один путь, по которому можно увеличить
поток
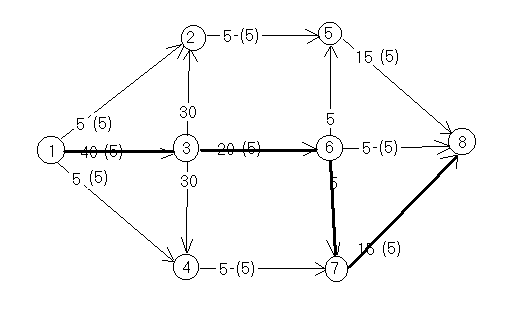
Теперь при поиске вершин, в которых можно создать избыток потока, получим
с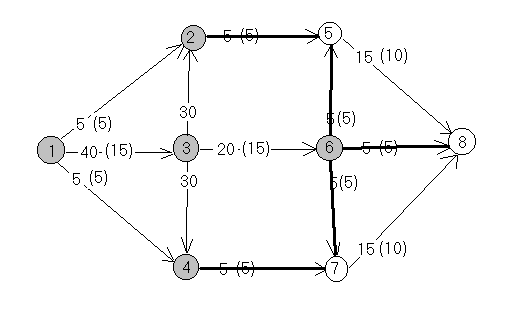
ледующий
граф. Цветом выделены все вершины в
которых можно получить избыточный
поток. Все ребра, соединяющие помеченные
и непомеченные вершины входят в
минимальный разрез. Размер разреза
равен размеру потока и они равны 25.
Решить задачу о назначениях, продемонстрировав работу венгерского алгоритма.
Пример. Задана матрица для задачи о назначениях
|
1 |
2 |
3 |
4 |
5 |
A |
12 |
3 |
4 |
6 |
11 |
B |
3 |
12 |
6 |
10 |
5 |
C |
6 |
6 |
9 |
2 |
10 |
D |
3 |
8 |
11 |
8 |
6 |
E |
5 |
9 |
15 |
9 |
8 |
Решение Находим минимальные элементы в каждой строке и отнимаем их от всех элементов строки. Аналогичную операцию выполняем для столбцов
|
1 |
2 |
3 |
4 |
5 |
A |
9 |
0 |
0 |
3 |
6 |
B |
0 |
9 |
2 |
7 |
0 |
C |
4 |
4 |
6 |
0 |
6 |
D |
0 |
5 |
7 |
5 |
1 |
E |
0 |
4 |
9 |
4 |
1 |
Строим двудольный граф и ищем для него максимальное паросочетание и минимальное контролирующее множество
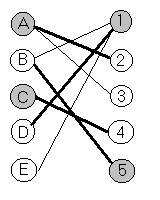
Помечаем в таблице элементы находящиеся на пересечении непомеченных строк и столбцов
|
1 |
2 |
3 |
4 |
5 |
A |
9 |
0 |
0 |
3 |
6 |
B |
0 |
9 |
2 |
7 |
0 |
C |
4 |
4 |
6 |
0 |
6 |
D |
0 |
5 |
7 |
5 |
1 |
E |
0 |
4 |
9 |
4 |
1 |
Минимальный элемент в помеченной части — 2. Отнимаем его от всех помеченных строк и прибавляем ко всем непомеченным столбцам.
|
1 |
2 |
3 |
4 |
5 |
A |
11 |
0 |
0 |
3 |
8 |
B |
0 |
7 |
0 |
5 |
0 |
C |
6 |
4 |
6 |
0 |
8 |
D |
0 |
3 |
5 |
3 |
1 |
E |
0 |
2 |
7 |
2 |
1 |
Строим двудольный граф и ищем для него максимальное паросочетание и минимальное контролирующее множество
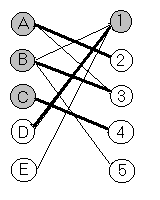
Помечаем в таблице элементы находящиеся на пересечении непомеченных строк и столбцов
|
1 |
2 |
3 |
4 |
5 |
A |
11 |
0 |
0 |
3 |
8 |
B |
0 |
7 |
0 |
5 |
0 |
C |
6 |
4 |
6 |
0 |
8 |
D |
0 |
3 |
5 |
3 |
1 |
E |
0 |
2 |
7 |
2 |
1 |
Минимальный элемент в помеченной части — 1. Отнимаем его от всех помеченных строк и прибавляем ко всем непомеченным столбцам.
|
1 |
2 |
3 |
4 |
5 |
A |
12 |
0 |
0 |
3 |
8 |
B |
1 |
7 |
0 |
5 |
0 |
C |
7 |
4 |
6 |
0 |
8 |
D |
0 |
2 |
4 |
2 |
0 |
E |
0 |
1 |
6 |
1 |
0 |
Строим двудольный граф и ищем для него максимальное паросочетание и минимальное контролирующее множество
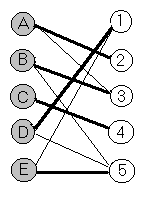
Паросочетание максимально, следовательно план (A,2),(B,3),(C,4),(D,1),(E,5) минимальный и его стоимость 22.
Построить код Прюфера для заданного дерева.
Пример. Дерево задано списком смежных вершин
1 |
5 |
2 |
5,8 |
3 |
4,5,7 |
4 |
3 |
5 |
1,2,3 |
6 |
8 |
7 |
3 |
8 |
2,6 |
Решение. 5 3 8 3 5 2 [8]
Построить дерево по коду Прюфера
Пример 5 3 8 3 5 2
Ответ
1 |
5 |
2 |
5,8 |
3 |
4,5,7 |
4 |
3 |
5 |
1,2,3 |
6 |
8 |
7 |
3 |
8 |
2,6 |
Определить является ли заданный граф планарным. Если граф не является планарным, то показать это с использованием критерия Понтрягина
Пример Граф задан списком смежных вершин
1 |
2,3,7,8 |
2 |
1,5 |
3 |
1,4,6 |
4 |
3,5,7,8 |
5 |
2,4,6,7 |
6 |
3,5,7,8 |
7 |
1,5,4,6 |
8 |
1,4,6 |
Решение Удалив вершину
3, и ребро (5,7) получим граф, заданный
следующим списком. Этот граф гомеоморфен
графу
поэтому по критерию Понтрягина он не
планарен.
1 |
2,7,8 |
2 |
1,5 |
|
|
4 |
5,7,8 |
5 |
2,4,6 |
6 |
5,7,8 |
7 |
1,4,6 |
8 |
1,4,6 |
Найти количество вершин(граней, ребер) у выпуклого многогранника.
Пример. В выпуклом многограннике 10 вершин и 8 граней. Сколько у него ребер?
Решение. По формуле Эйлера r=v+g-2, ребер 16.
Построить таблицу истинности для булевой функции, заданной формулой
Пример.
Найти
Решение
|
|
|
g |
h |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
|
+ |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
x |
y |
z |
f |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
Найти фиктивные переменные булевых функций
Пример.
Решение
.
Переменная y
фиктивная, x,z
— существенные.
Проверить эквивалентность булевых функций
Пример.
Решение. В функции f
фиктивна переменная y,
в функции g
— w.
После удаления фиктивных переменных
Функции эквивалентны.
Привести булеву функцию к ДНФ методом эквивалентных преобразований
Пример
Решение
Привести булеву функцию к полиному Жегалкина методом эквивалентных преобразований
Пример
Решение
Построить СДНФ (СКНФ) методом эквивалентных преобразований
Пример
Решение
Построить полином Жегалкина
Пример. Построить
полином Жегалкина для функции
Решение. Метод
разложения.
Метод треугольника
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
yz |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
|
|
|
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
|
|
xz |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
xy |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|
Проверить базис на полноту
Пример. Является ли
полным базис следующих функций
Решение
|
T0 |
T1 |
M |
L |
S |
(0001) |
+ |
+ |
+ |
- |
- |
(0111) |
+ |
+ |
+ |
- |
- |
(11101000) |
- |
- |
- |
- |
+ |
Базис полный
Найти минимальную ДНФ булевой функции
Пример
Решение
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
СДНФ
Тупиковая ДНФ
Минимальная ДНФ
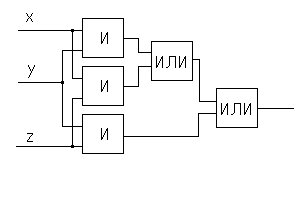
Построить таблицу истинности для функции, заданной схемой функциональных элементов.
Пример.
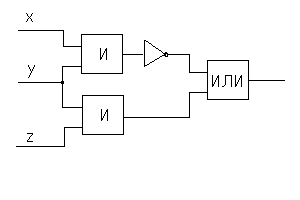
Решение
x |
y |
z |
f |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
Построить схему функциональных элементов для заданной функции.
Пример
Решение
