Перетворення спектру та високочастотна фільтрація вихідних даних
гц |
0 |
1 |
.. |
5 |
. |
20 |
… |
40 |
… |
60 |
.. |
80 |
.. |
95 |
… |
99 |
|
10 |
0 |
0 |
15 |
0 |
40 |
0 |
120 |
0 |
120 |
0 |
40 |
0 |
15 |
0 |
0 |
град |
0 |
0 |
0 |
-180 |
0 |
-90 |
0 |
90 |
0 |
-90 |
0 |
90 |
0 |
-180 |
0 |
0 |
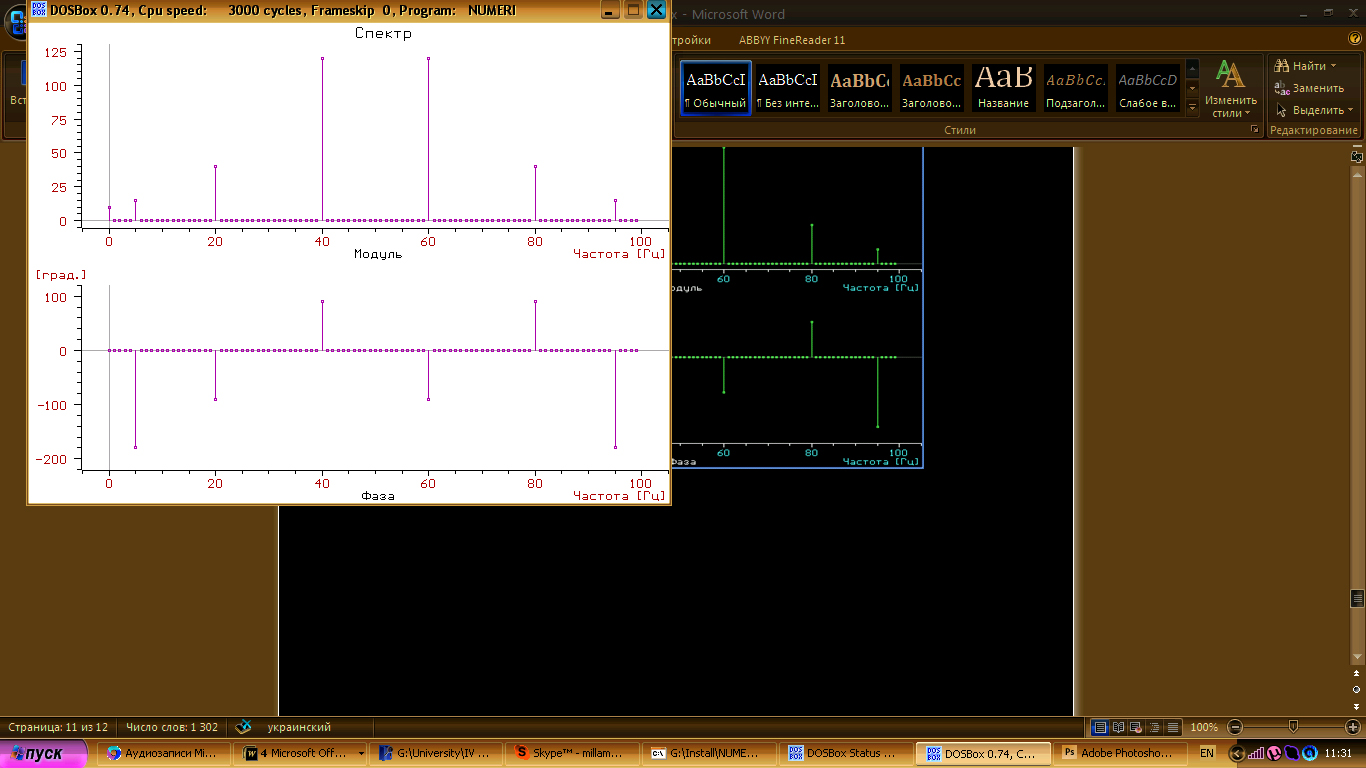
Амплітудний та фазовий спектри:
Спектр сигналу заданий на проміжку [0, 99]Гц із інтервалом 1гц.
Кількість точок N=100.
Частота дискретизації
Період дискретизації
Сигнал має чотири складових.
Перша складова
гармонійна з амплітудою
на частотах 5 Гц і 95 Гц, з фазами -180 та
-180. Отже, можна зробити висновок, що це
від`ємна
косинусоїда -0.3*cos(2π*5*x)
Друга складова
гармонійна з амплітудою
на частотах 20 Гц і 80 Гц, з фазами -90 та
90. Отже, можна зробити висновок, що це
додатня
синусоїда 0.8*sin(2π*20*x)
Третя складова
гармонійна з амплітудою
на частотах 40 Гц і 60 Гц, з фазами 90 та
-90. Отже, можна зробити висновок, що це
від`ємна
синусоїда -2.4*sin(2π*40*x)
Четверта складова
на частоті 0 Гц – стала складова сигналу
з амплітудою
Отже, аналітичний вираз для часового сигналу матиме вигляд:
Y = 0.1 - 0.3*cos(2π*5*x) + 0.8*sin(2π*20*x) - 2.4*sin(2π*40*x)
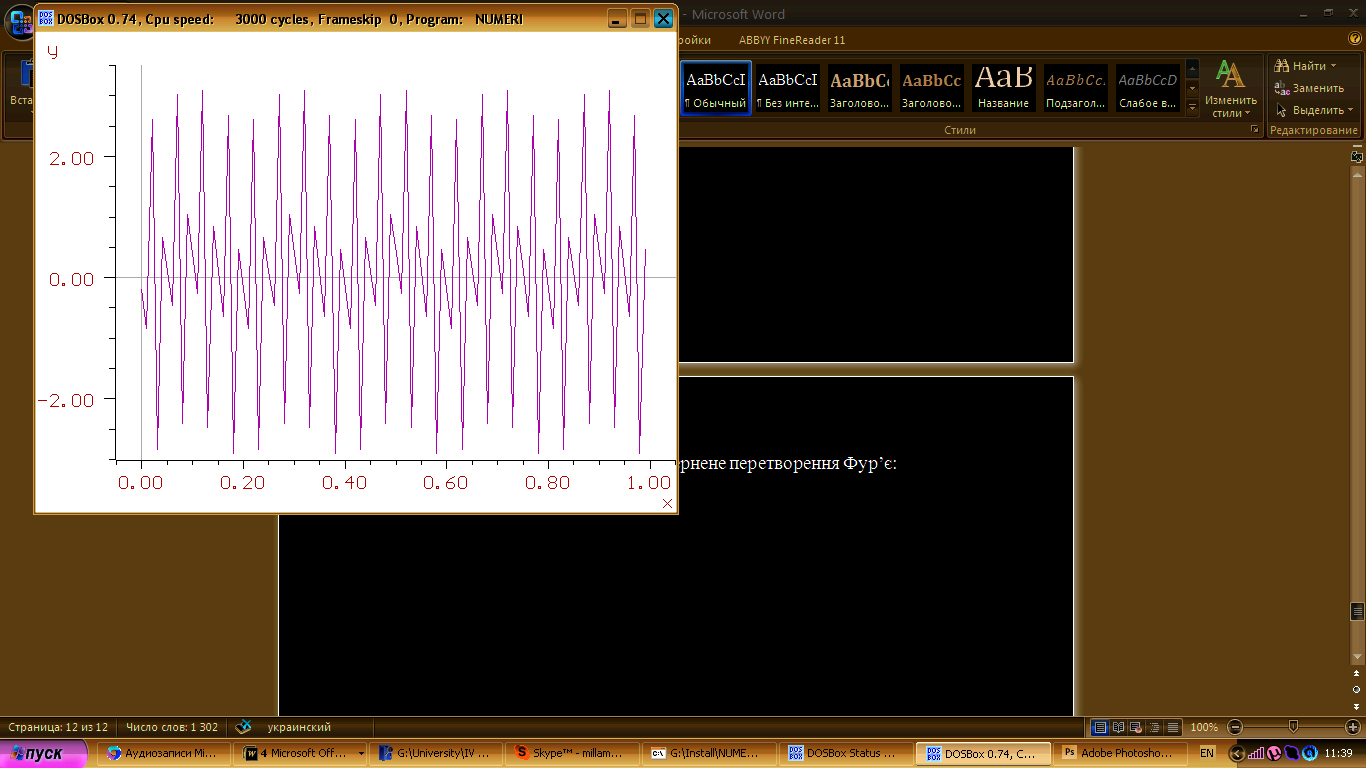
Графік аналітичної функції:
Спектр сигналу:
Графік функції отриманої через обернене перетворення Фур’є:
Високочастотна фільтрація методом перетворення спектру
Пари 40, 60 – високочастотні
Пара Дійсна частина Уявна частина
40 0 120
60 0 -120
Спектр високочастотної складової
Зі спектру видно, що високочастотна складова -2.4*sin(2π*40*x) повністю відновлюється