9 Вопрос

Квантовая теория теплоёмкостей Эйнштейна была создана Эйнштейном в 1907 году при попытке объяснить экспериментально наблюдаемую зависимость теплоёмкости от температуры.

При разработке теории Эйнштейн опирался на следующие предположения:

Атомы в кристаллической решетке ведут себя как гармонические осцилляторы, не взаимодействующие друг с другом.

Частота колебаний всех осцилляторов одинакова.

Число осцилляторов в 1 моле вещества равно , где N_a — число Авогадро.

Энергия их квантована: ,

Число осцилляторов с различной энергией определяется распределением Больцмана:

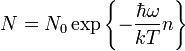
Внутренняя энергия 1 моля вещества:

находится из соотношения для среднего значения: и составляет: , отсюда: .

Определяя теплоёмкость как производную внутренней энергии по температуре, получаем окончательную формулу для теплоёмкости: .

Согласно модели, предложенной Эйнштейном, при абсолютном нуле температуры теплоёмкость стремится к нулю, при больших температурах, напротив, выполняется закон Дюлонга — Пти. Величина иногда называется температурой Эйнштейна.

Недостатки теории

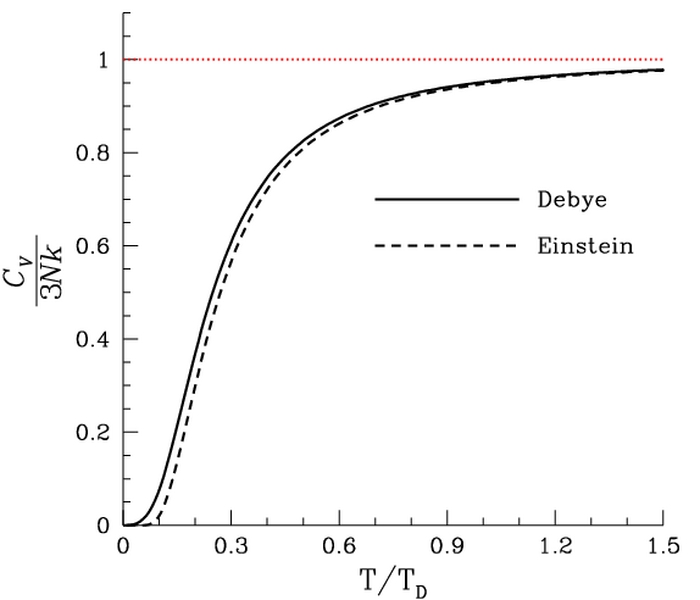
Расхождение теорий Эйнштейна и Дебая

Теория Эйнштейна, однако, недостаточно хорошо согласуется с результатами экспериментов в силу неточности некоторых предположений Эйнштейна, в частности, предположения о равенстве частот колебаний всех осцилляторов. Более точная теория была создана Дебаем в 1912 году.

10 Вопрос

В термодинамике и физике твёрдого тела модель Дебая — метод, развитый Дебаем в 1912 г. для оценки фононного вклада в теплоёмкость твёрдых тел. Модель Дебая рассматривает колебания кристаллической решётки как газ квазичастиц — фононов. Эта модель правильно предсказывает теплоёмкость при низких температурах, которая, согласно закону Дебая, пропорциональна . В пределе высоких температур теплоёмкость стремится к 3R, согласно закону Дюлонга — Пти.

При тепловом равновесии энергия E набора осцилляторов с различными частотами равна сумме их энергий:

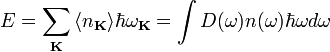
где — число мод нормальных колебаний на единицу длины интервала частот, — количество осцилляторов в твёрдом теле, колеблющихся с частотой ω.

Функция плотности в трёхмерном случае имеет вид:

где V — объём твёрдого тела, — скорость звука в нём.

Значение квантовых чисел вычисляются по формуле Планка:

Тогда энергия запишется в виде

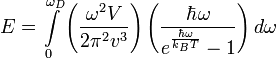
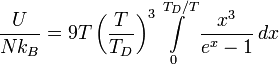
где — температура Дебая, — число атомов в твёрдом теле, — постоянная Больцмана.

Дифференцируя внутреннюю энергию по температуре получим:

Молярная теплоёмкость твёрдого тела в теории Дебая

В модели Дебая учтено, что теплоёмкость твёрдого тела — это параметр равновесного состояния термодинамической системы. Поэтому волны, возбуждаемые в твёрдом теле элементарными осцилляторами, не могут переносить энергию. То есть они являются стоячими волнами. Если твёрдое тело выбрать в виде прямоугольного параллелепипеда с рёбрами a, b, c, то условия существования стоячих волн можно записать в виде:

n1•λx/2=a; n2•λy/2=b; n3•λz/2=c; (n1, n2, n3 — целые числа)

Перейдём к пространству, построенному на волновых векторах. Поскольку K=2π/λ, то

Kx=2π/λx=π•n1/a; Ky=2π/λy=π•n2/b; Kz=2π/λz=π•n3/c

Таким образом, в твёрдом теле могут существовать осцилляторы, с частотами, изменяющимися дискретно. Одному осциллятору в К-пространстве соответствует ячейка с объёмом

τ=∆Kx•∆Ky•∆Kz= ,

где

∆Kx=π/a; ∆Ky=π/b; ∆Kz=π/c

В к-пространстве осцилляторам с частотами в интервале (ω, ω+dω) соответствует один октант сферического слоя с объёмом

dVk=4πK2dK/8=πK2dK/2

В этом объёме количество осцилляторов равно

dNk=dVk/τ=

Учтём, что каждый осциллятор генерирует 3 волны: 2 поперечные и одну продольную. При этом K||=ω/v||, K⊥=ω/v⊥

Найдём внутреннюю энергию одного моля твёрдого тела. Для этого запишем взаимосвязь между волновым числом, скоростью распространения волн и частотой.

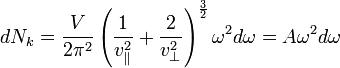
Колебания в твёрдом теле ограничены максимальным значением частоты . Определим граничную частоту из условия:

Отсюда:

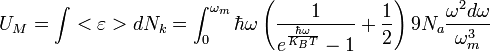
<є> — средняя энергия квантового осциллятора (см. модель теплоёмкости Эйнштейна).

Кв — постоянная Больцмана.

Na — число Авогадро.

В последнем выражении сделаем следующую замену переменных:

;ℏω=KВθ; ;

Θ — температура Дебая

Теперь для UM получим

Наконец, для молярной теплоёмкости получаем

C=dUM/dT=3R

Легко проверить, что при условии T→∞ C→3R, а при условии T→0 C→ ~T3

Интеграл может быть взят методами теории функций комплексной переменной или с использованием дзета-функции Римана. Таким образом, теория Дебая соответствует результатам экспериментов.