24 Вопрос

Эффе́кт Зе́емана — расщепление линий атомных спектров в магнитном поле.

Обнаружен в 1896 г. Зееманом для эмиссионных линий натрия.

Эффект обусловлен тем, что в присутствии магнитного поля квантовая частица, обладающая спиновым магнитным моментом, приобретает дополнительную энергию пропорциональную его магнитному моменту Приобретённая энергия приводит к снятию вырождения атомных состояний по магнитному квантовому числу и расщеплению атомных линий.

Природа эффекта

В классическом представлении

Атом, как известно, можно рассматривать как классический гармонический осциллятор, и его уравнение движения в присутствии магнитного поля направленного вдоль оси Z, можно рассматривать в виде:

где — скорость вращения электрона вокруг ядра, — масса электрона, — резонансная частота электронного дипольного перехода. Последний член в уравнении обусловлен силой Лоренца.

Введём величину, называемую ларморовской частотой

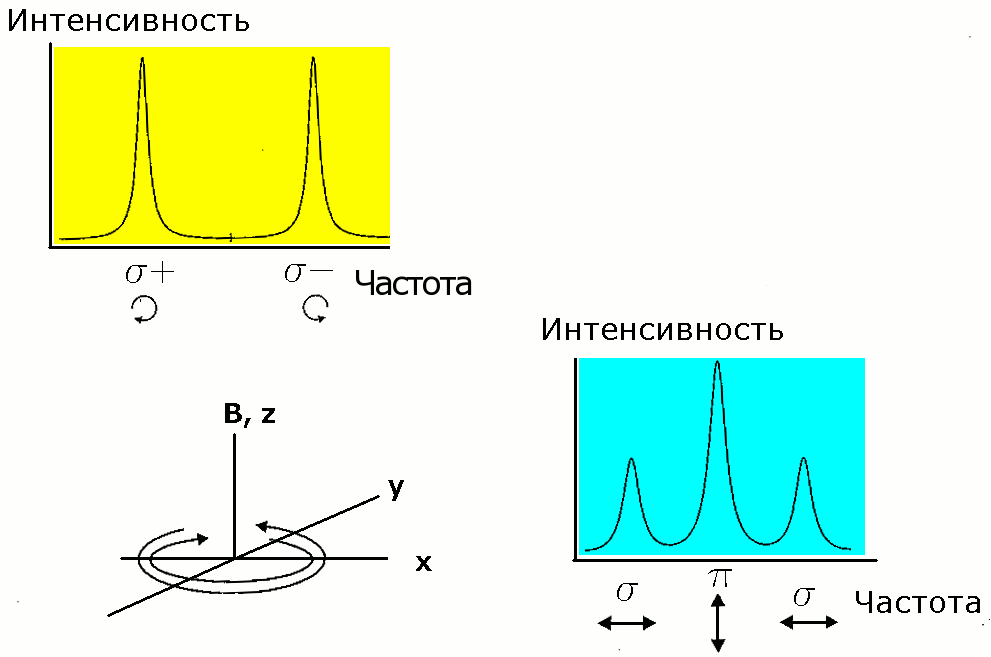Поляризация и спектр Зееман-эффекта, детектируемые с различных направлениях наблюдения: * картинка с жёлтым фоном — наблюдение ведётся в направлении магнитного поля. В этом случае в спектре флуоресценции атомарных паров детектируется две частоты c круговой поляризацией и * картинка с синим фоном — наблюдение ведётся перпендикулярно направлению магнитного поля. В этом случае в спектре флуоресценции атомарных паров детектируются три частоты, имеющие линейную поляризацию σ и π.

Решая уравнение движения, легко обнаружим, что резонансная частота дипольного момента в присутствии магнитного поля расщепляется на три частоты Таким образом, в магнитном поле электрон вместо простого вращения вокруг ядра атома начинает совершать сложное движение относительно выделенного магнитным полем направления Z. Электронное облако атома прецессирует вокруг этой оси с частотой Лармора

Такая простая модель объясняет наблюдаемое в экспериментах изменение поляризации флуоресценции атомарных паров в зависимости от направления наблюдения. Если смотреть вдоль оси Z, то на частоте никакой атомной флуоресценции наблюдаться не будет, так как атомный диполь на этой частоте колеблется вдоль оси магнитного поля, а его излучение распространяется в направлении, перпендикулярном этой оси. На частотах наблюдается право- и левовращающая поляризации, так называемые σ− и π+-поляризации.

Если же смотреть вдоль осей X или Y, то наблюдается линейная поляризация (π и σ соответственно) на всех трёх частотах и . Вектор поляризации света π направлен вдоль магнитного поля, а σ — перпендикулярно.

В квантовом представлении

Полный гамильтониан атома в магнитном поле имеет вид:

где H₀ — невозмущенный гамильтониан атома и V_M — возмущение, созданное магнитным полем:

Здесь — магнитный момент атома, который состоит из электронной и ядерной частей. Ядерным магнитным моментом, который на несколько порядков меньше электронного, можно пренебречь. Следовательно,

где — магнетон Бора, — полный электронный угловой момент, и — фактор.

Оператор магнитного момента электрона является суммой орбитального углового и спинового углового моментов, умноженных на соответствующие гиромагнитные отношения:

где и gs ≈ 2,0023192; последнюю величину называют аномальным гиромагнитным отношением; отклонение от 2 появляется из-за квантово-электродинамических эффектов. В случае LS-связи для расчета полного магнитного момента суммируются все электроны:

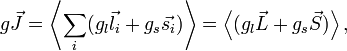
Где и — полный орбитальный и спиновый моменты атома, и усреднение делается по атомному состоянию с данной величиной полного углового момента.

Нормальный эффект Зеемана

Если член взаимодействия V_M мал (меньше тонкой структуры то есть ), его можно рассматривать как возмущение и этот случай называют нормальным эффектом Зеемана. Нормальный эффект Зеемана наблюдается:

при переходах между синглетными термами ( );

при переходах между уровнями и ;

при переходах между уровнями и , поскольку не расщепляется, а расщепляется на три подуровня.

Расщепление связано с чисто орбитальным или чисто спиновым магнитным моментами. Это наблюдается в синглетах He и в группе щелочноземельных элементов, а также в спектрах Zn, Cd, Hg.

и поляризация наблюдаются при изменении проекции магнитного момента на и , соответственно.

Аномальный эффект Зеемана

Для всех несинглетных линий спектральные линии атома расщепляются на значительно большее чем три количество компонент, а величина расщепления кратна нормальному расщеплению . В случае аномального эффекта величина расщепления сложным образом зависит от квантовых чисел . Как указано ранее, приобретенная электроном в магнитном поле дополнительная энергия V_M пропорциональна — фактору, который называют множителем Ланде (гиромагнитный множитель) и который дается формулой

где L — значение орбитального момента атома, S — значение спинового момента атома, J — значение полного момента.

Впервые этот множитель ввел Ланде. Работы Ланде являлись продолжением работ Зеемана, поэтому спектры, полученные Ланде в магнитном поле, называют аномальным эффектом Зеемана. Заметим, что эксперимент Зеемана сделан при , то есть , поэтому никакой надобности в множителях не возникало.

Таким образом, вырожденный энергетический уровень расщепляется на равноотстояших зеемановских подуровня (где J — максимальное значение модуля магнитного квантового числа .

Эффект Пашена-Бака

В эффекте Пашена-Бака, (но все еще меньше величины магнитного поля H₀). В сверхсильных магнитных полях V_M превышает поле H₀. В этом случае атом больше не существует в обычном смысле. В это случае говорят об уровнях Ландау.

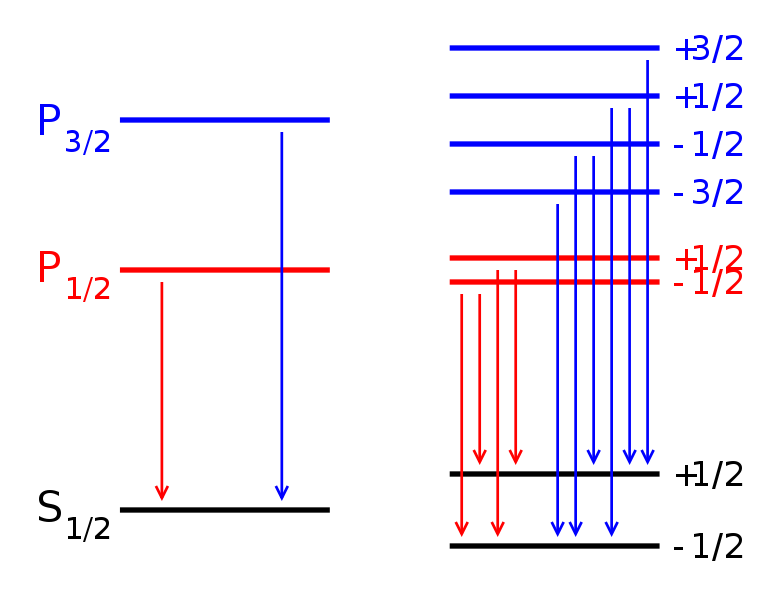
Спектр для нормального (слева) и аномального (справа) случаев.

Таким образом вырожденный энергетический уровень расщепляется на 2J+1 равноотстояших зеемановских подуровней (где J — максимальное значение модуля магнитного квантового числа .