23 Вопрос

Парамагнетики — вещества, которые намагничиваются во внешнем магнитном поле в направлении внешнего магнитного поля. Парамагнетики относятся к слабомагнитным веществам, магнитная проницаемость незначительно отличается от единицы .

Термин «Парамагнетизм» ввёл в 1845 году Майкл Фарадей, который разделил все вещества (кроме ферромагнитных) на диа- и парамагнитные.

Атомы (молекулы или ионы) парамагнетика обладают собственными магнитными моментами, которые под действием внешних полей ориентируются по полю и тем самым создают результирующее поле, превышающее внешнее. Парамагнетики втягиваются в магнитное поле. В отсутствие внешнего магнитного поля парамагнетик не намагничен, так как из-за теплового движения собственные магнитные моменты атомов ориентированы совершенно беспорядочно.

К парамагнетикам относятся алюминий (Al), платина (Pt), многие другие металлы (щелочные и щелочно-земельные металлы, а также сплавы этих металлов), кислород (О2), оксид азота (NO), оксид марганца (MnO), хлорное железо (FeCl) и др.

Парамагнетиками становятся ферро- и антиферромагнитные вещества при температурах, превышающих, соответственно, температуру Кюри или Нееля (температуру фазового перехода в парамагнитное состояние).

Парамагнетизм (от пара... и магнетизм), свойство тел, помещенных во внешнее магнитное поле, намагничиваться (приобретать магнитный момент)в направлении, совпадающем с направлением этого поля. Т. о., внутри парамагнитного тела (парамагнетика) к действию внешнего поля прибавляется действие возникшей намагниченности J. В этом отношении П. противоположен диамагнетизму, при котором возникающий в теле под действием поля магнитный момент ориентирован навстречу направлению напряжённости внешнего магнитного поля Н.Поэтому парамагнитные тела притягиваются к полюсам магнита (откуда название "П."), а диамагнитные — отталкиваются. Характерным для парамагнетиков свойством намагничиваться по полю обладают также ферромагнетики и антиферромагнетики. Однако в отсутствие внешнего поля намагниченность парамагнетиков равна нулю и они не обладают магнитной структурой (взаимной упорядоченной ориентацией магнитных моментов атомов), в то время как при Н = 0 ферро- и антиферромагнетики сохраняют магнитную структуру. Термин "П." ввёл в 1845 М. Фарадей, который разделил все вещества (кроме ферромагнитных) на диа- и парамагнитные. П. характерен для веществ, частицы которого (атомы, молекулы, ионы, ядра атомов) обладают собственным магнитным моментом, но в отсутствие внешнего поля эти моменты ориентированы хаотически, так что J = 0. Во внешнем поле магнитные моменты атомов парамагнитных веществ ориентируются преимущественно по полю. В слабых полях намагниченность парамагнетиков растет с ростом поля по закону J = c Н, где c — магнитная восприимчивость 1 моля вещества, для парамагнетиков всегда положительная и обычно равная по порядку величины 10-5 — 10-3. Если поле очень велико, то все магнитные моменты парамагнитных частиц ориентируются строго по полю (достигается магнитное насыщение). С повышением температуры Т при неизменной напряжённости поля возрастает дезориентирующее действие теплового движения частиц и магнитная восприимчивость убывает — в простейшем случае по Кюри закону c = С/Т (С — постоянная Кюри, зависящая от природы вещества). Отклонения от закона Кюри (см. Кюри — Вейса закон) в основном связаны с взаимодействием частиц (влиянием кристаллического поля). П. свойствен: многим чистым элементам в металлическом состоянии (щелочные металлы, щёлочноземельные металлы, некоторые металлы переходных групп с незаполненным d-слоем или f-слоем электронной оболочки — группы железа, палладия, платины, редкоземельных элементов, актиноидов; а также сплавы этих металлов); солям группы железа, группы редкоземельных элементов от Ce до Yb и актиноидов и их водным растворам; парам щелочных металлов и молекулам газов (например, O2 и NO); небольшому числу органических молекул ("бирадикалам"); ряду комплексных соединений. Парамагнетиками становятся ферро- и антиферромагнитные вещества при температурах, превышающих, соответственно, температуру Кюри или Нееля (температуру фазового перехода в парамагнитное состояние).

Существование у атомов (ионов) магнитных моментов, обусловливающих П. веществ, может быть связано с движением электронов в оболочке атома (орбитальный П.), со спиновым моментом самих электронов (спиновый П.), с магнитными моментами ядер атомов (ядерный П.). Магнитные моменты атомов, ионов, молекул создаются в основном спиновыми и орбитальными моментами их электронных оболочек. Они примерно в тысячу раз превосходят магнитные моменты атомных ядер (см. Магнетон). П. металлов слагается в основном из П., свойственного электронам проводимости (так называемый парамагнетизм Паули), и П. электронных оболочек атомов (ионов) кристаллической решётки металла. Поскольку движение электронов проводимости металлов практически не меняется при изменении температуры, П., обусловленный электронами проводимости, от температуры не зависит. Поэтому, например, щелочные и щёлочноземельные металлы, у которых электронные оболочки ионов лишены магнитного момента, а П. обусловлен исключительно электронами проводимости, обладают магнитной восприимчивостью, не зависящей от температуры. В тех веществах, у которых нет электронов проводимости и магнитным моментом обладает лишь ядро (например, у изотопа гелия 3He), П. крайне мал (c~10-9—10-12) и может наблюдаться лишь при сверхнизких температурах (Т < 0,1К). Парамагнитная восприимчивость диэлектриков, согласно классической теории П. Ланжевена (1906), определяется формулой c = Nma2/3kT, где N — число магнитных атомов в 1 моле вещества, ma — магнитный момент атома, к — Больцмана постоянная. Эта формула была получена методами статистической физики для системы практически не взаимодействующих атомов, находящихся в слабом магнитном поле или при высокой температуре (когда mаН << kT). Она даёт теоретическое объяснение Кюри закону. В сильных магнитных полях или при низких температурах maH >> kT) намагниченность парамагнитных диэлектриков стремится к Nma2(к насыщению). Квантовая теория П., учитывающая квантование пространственное момента mа (Л. Бриллюэн, 1926), даёт аналогичное выражение для восприимчивости (диэлектриков (при maH << kT): c =NJ (J + 1)mа2gj2/3кТ, где J — квантовое число, определяющее полный момент количества движения атома, gj — Ланде множитель. Парамагнитная восприимчивость полупроводников cпэ, обусловленная электронами проводимости, в простейшем случае зависит от температуры Т экспоненциально

cпэ=АТ^1/2 exp (—DE/2kT), где А — константа вещества, DЕ — ширина запрещенной зоны полупроводника. Особенности индивидуального строения полупроводников сильно искажают эту зависимость. В простейшем случае для металлов (без учёта Ландау диамагнетизма и взаимодействия электронов) cмэ = 3Nm2э/2Eo, где Eo — Ферми энергия, mэ — магнитный момент электрона (cмэ не зависит от температуры). Ядерный П. при отсутствии сильного взаимодействия между спинами ядер и электронными оболочками атомов характеризуется величиной cя = Nm2я \3kT, которая приблизительно в 106 раз меньше электронной парамагнитной восприимчивости (mэ~103 mя). Изучение П. различных веществ, а также электронного парамагнитного резонанса (резонансного поглощения парамагнетиками энергии электромагнитного поля) позволяет определять магнитные моменты отдельных атомов, ионов, молекул, ядер, изучать строение сложных молекул и молекулярных комплексов, а также осуществлять тонкий структурный анализ материалов, применяемых в технике. В физике парамагнитные вещества используют для получения сверхнизких температур (ниже 1 К, см. Магнитное охлаждение). Историю развития учения о П. см. в ст. Магнетизм.

Закон Кюри — физический закон, описывает магнитную восприимчивость парамагнетиков, которая при постоянной температуре для этого вида материалов приблизительно прямо пропорциональна приложенному магнитному полю. Закон Кюри постулирует, что при изменении температуры и постоянном внешнем поле, степень намагниченности парамагнетиков обратно пропорциональна температуре:

где в единицах Международной системе единиц (СИ): M — получаемая намагниченность материала; B — магнитное поле, измеренное в Теслах; T — абсолютная температура в Кельвинах; C — постоянная Кюри данного материала. Это соотношение, полученное экспериментально П. Кюри, выполняется только при высоких температурах или слабых магнитных полях. В обратном случае — то есть при низких температурах или при сильных полях — намагниченность не подчиняется этому закону.

Вывод закона с использованием квантовой статистической механики

М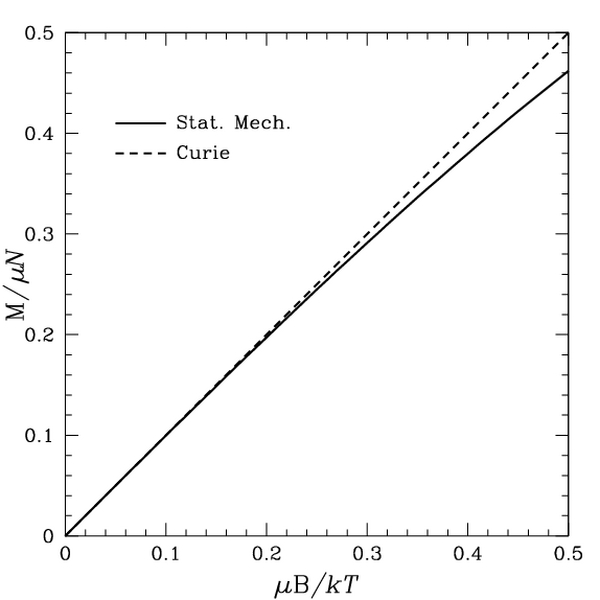 агнитная восприимчивость парамагнетика как функция температуры.

Простые модели парамагнетиков основываются на предположении, что эти материалы состоят из частей или областей (парамагнетонов), которые не взаимодействуют друг с другом. Каждая область имеет собственный магнитный момент, который можно обозначить векторной величиной . Энергия момента магнитного поля может быть записана следующим образом:

Области с двумя состояниями (спин-1/2)

Для того, чтобы упростить вывод, предположим, что каждая из областей рассматриваемого парамагнетика имеет два состояния момента, направление которого может совпадать с направлением магнитного поля или быть направленным в противоположную сторону. В данном случае возможны только два значения магнитного момента , и два значения энергии: и . При поиске магнитной восприимчивости парамагнетика определяется вероятность для каждой области оказаться в состоянии, сонаправленном магнитному полю. Другими словами, определяется математическое ожидание намагниченности материала :

где вероятность системы описывается распределением Больцмана, статистическая сумма Z обеспечивает нормализацию вероятностей. Нормирующая функция для одной области может быть представлена следующим образом:

Таким образом, в двухспиновой модели мы имеем:

Используя полученное выражение для одной области, получаем магнитную восприимчивость всего материала:

Выведенная выше формула носит название уравнения Ланжевена для парамагнетиков. П. Кюри в ходе экспериментов обнаружил приближение к этому закону, которое выполнялось при высоких температурах и слабых магнитных полях. Предположим, что абсолютное значение температуры T велико, а B мало. В данном случае, иногда называемом режимом Кюри, величина аргумента гиперболического тангенса мала:

И так как известно, что в случае выполняется соотношение:

получаем результат:

где константа Кюри равна . Также следует отметить, что в противоположном случае низких температур и сильных полей, и имеют тенденцию принимать максимальные значения, что соответствует случаю, когда все области имеют магнитный момент, совпадающий по направлению с магнитным полем.

Общий случай

В общем случае произвольного распределения направлений магнитных моментов формула становится несколько более сложной (см. англ. Brillouin function). Как только значение спина приближается к бесконечности, формула для магнитной восприимчивости принимает классический вид.

Получение с помощью классической статистической механики

Альтернативный подход предполагает, что парамагнетоны представляют из себя области со свободно вращающимися магнитными моментами. В данном случае их положение определяется углами в сферических координатах, а энергия одной области представляется в виде:

где — угол между направлением магнитного момента и направлением магнитного поля, которое, предположим, направлено вдоль координаты z. Соответствующая функция для одной области будет иметь вид:

Как видно, в данном случае нет явной зависимости от угла , и мы также можем осуществить замену переменной , что позволяет получить:

Математическое ожидание компоненты z будет соответствовать степени намагниченности, а остальные две обратятся в нуль после интегрирования по :

Для упрощения вычислений, запишем выражение в дифференциальной форме по переменной Z:

что дает:

где L носит название функции Ланжевена (см. Ланжевен):

Эта функция имеет сингулярность (разрыв) для маленьких значений x, но на самом деле нет, так как две сингулярные компоненты с противоположным знаком сохраняют непрерывность функции. На самом деле, её поведение при небольших значениях аргумента , что сохраняет действие закона Кюри, но с втрое ме́ньшим постоянным множителем-константой Кюри. В случае предела с больши́м значением аргумента применение этой функции также возможно.

Применения

Сохранение закона Кюри для парамагнетиков в слабом магнитном поле позволяет их использование в качестве магнитных термометров.

Магнитный момент

Элементарные частицы обладают внутренним квантовомеханическим свойством известным как спин. Оно аналогично угловому моменту объекта вращающегося вокруг собственного центра масс, хотя строго говоря, эти частицы являются точечными и нельзя говорить об их вращении. Спин измеряют в единицах приведённой планковской постоянной ( ), тогда электроны, протоны и нейтроны имеют спин равный ½ . В атоме электроны обращаются вокруг ядра и обладают орбитальным угловым моментом помимо спина, в то время как ядро само по себе имеет угловой момент благодаря ядерному спину.[28]

Магнитное поле, создаваемое магнитным моментом атома, определяется этими различными формами углового момента, как и в классической физике вращающиеся заряженные объекты создают магнитное поле. Однако, наиболее значительный вклад происходит от спина. Благодаря свойству электрона, как и всех фермионов, подчиняться правилу запрета Паули, по которому два электрона не могут находиться в одном и том же квантовом состоянии, связанные электроны спариваются друг с другом, и один из электронов находится в состоянии со спином вверх, а другой — с противоположной проекцией спина — состояние со спином вниз. Таким образом магнитные моменты электронов сокращаются, уменьшая полный магнитный дипольный момент системы до нуля в некоторых атомах с чётным числом электронов.[29]

В ферромагнитных элементах, таких как железо, нечётное число электронов приводит к появлению неспаренного электрона и к ненулевому полному магнитному моменту. Орбитали соседних атомов перекрываются, и наименьшее энергетическое состояние достигается, когда все спины неспаренных электронов принимают одну ориентацию, процесс известный как обменное взаимодействие. Когда магнитные моменты ферромагнитных атомов выравниваются, материал может создавать измеримое макроскопическое магнитное поле. Парамагнитные материалы состоят из атомов, магнитные моменты которых разориентированы в отсутствии магнитного поля, но магнитные моменты отдельных атомов выравниваются при приложении магнитного поля.[29][30]

Ядро атома тоже может обладать ненулевым полным спином. Обычно при термодинамическом равновесии спины ядер ориентированы случайным образом. Однако, для некоторых элементов (таких как ксенон-129) возможно поляризовать значительную часть ядерных спинов для создания состояния с сонаправленными спинами —состояния называемого гиперполяризацией. Это состояние имеет важное прикладное значение в магнитно-резонансной томографии.