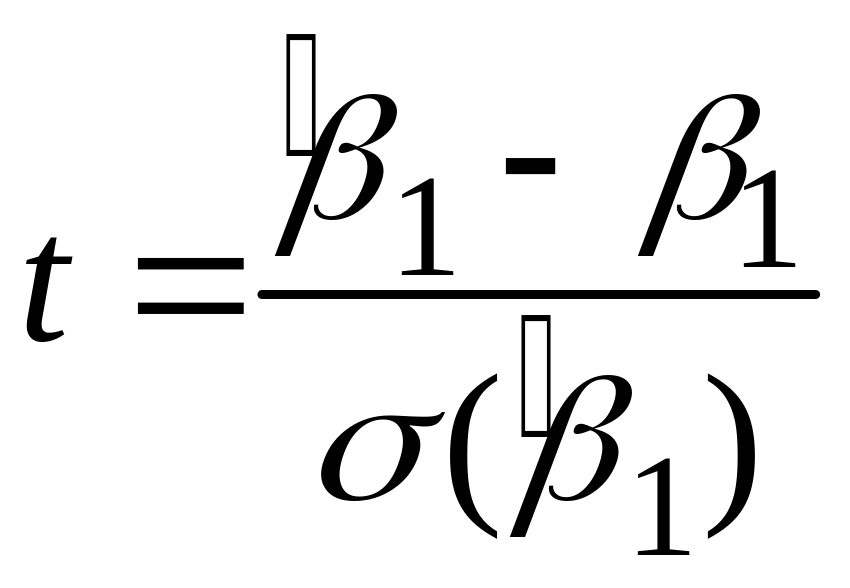- •Економетрика конспект лекцій
- •Зауваження................................................................................................118
- •1. Регресійний аналіз. Регресійний аналіз для двох змінних: основні ідеї
- •1.1. Гіпотетичний приклад
- •1.2. Концепція регресійної функції популяції (prf роpulation regression function)
- •1.3. Значення терміна “лінійність”
- •1.4. Стохастичні властивості prf
- •1.5. Важливість урахування складової стохастичного збурення
- •1.6. Вибіркова регресійна функція (srf)
- •2. Двовимірна регресійна модель. Задача оцінки
- •2.1. Метод найменших квадратів
- •Експериментальне визначення srf
- •2.2. Властивості оцінок за мнк
- •Дійсна й оцінена ціна будинку і його житлова площа у кв. Футах
- •Припущення 4 гомоскедастичність або рівність дисперсій
- •Це припущення не таке нешкідливе, як здається. Розглянемо рівняння
- •2.3. Точність або стандартна похибка оцінювачів за мнк
- •2.4. Властивості оцінювачів за мнк: теорія Гаусса-Маркова
- •2.5. Коефіцієнт детермінації : міра «якості підгонки»
- •2.6. Числовий приклад
- •2.7. Ілюстративні приклади
- •3. Інтервальні оцінки і перевірка гіпотез
- •3.1. Інтервальні оцінки: основні ідеї
- •3.2 Довірчі інтервали для регресійних коефіцієнтів і
- •Отже, наприклад, змінна
- •3.3. Довірчий інтервал для
- •3.4. Перевірка гіпотез: загальні зауваження
- •3.5. Перевірка гіпотез: підхід на основі довірчого інтервалу
- •3.6. Перевірка гіпотез: підхід, оснований на перевірці значимості
- •3.7. Перевірка значимості : хі-квадрат тест
- •3.8. Регресійний аналіз і аналіз дисперсії
- •Розглянемо таку змінну:
- •3.9. Застосування регресійного аналізу: проблема прогнозу
- •3.10. Форма звіту за результатами регресійного аналізу
- •3.11. Обчислення результатів регресійного аналізу
- •Залишки для проведення -тесту
- •4. Розвиток двовимірної лінійної моделі регресії
- •4.1. Регресія, що проходить через початок координат
- •4.2. Масштабування й одиниці вимірювання
- •Валові внутрішні приватні інвестиції (gpdi) і валовий національний продукт (gnp) у цінах 1972 р. У доларах сша, 1974–1983 рр.
- •4.3. Функціональний вид регресійної моделі
- •4.4. Вимірювання еластичності. Лінійно-логарифмічна модель
- •4.5. Напівлогарифмічні моделі. Визначення темпів зростання.
- •4.6. Обернені моделі
- •4.7. Зауваження щодо стохастичної складової
- •5. Множинний регресійний аналіз. Задача оцінювання
- •5.1. Модель із трьома змінними. Позначення і гіпотези
- •5.2. Інтерпретація рівняння множинної регресії
- •5.3. Значення частинних коефіцієнтів регресії
- •5.4. Оцінка частинних коефіцієнтів регресії за мнк
- •5.6. Проста регресія в контексті множинної регресії
- •5.7. R2 і скорегований r2
- •5.8. Частинні коефіцієнти кореляції
- •5.9. Виробнича функція Коба – Дугласа
- •5.10. Поліноміальная модель регресії
- •6. Припущення нормальності розподілу залишків
- •Витрати на споживання і особистий дохід у сша за 1956–1970 рр.
- •7. Перевірка гіпотез множинної регресії. Загальні зауваження
- •7.1. Перевірка гіпотези про частинний коефіцієнт регресії
- •7.2. Перевірка вибіркової регресії на загальну значущість
- •7.3. Перевірка на рівність двох коефіцієнтів регресії
- •7.4. Перевірка лінійних обмежень
- •Обчислимо
- •7.5. Перевірка структурної стабільності моделей регресії
- •Можна показати, що при виконанні згаданих припущень
- •7.6. Перевірка функціонального виду регресії. Вибір між лінійною моделлю регресії і лінійно-логарифмічною моделлю
- •8. Прогнозування в разі множинної регресії
- •9. Множинна регресія. Матричний метод
- •9.1. Лінійна модель регресії з k змінними
- •9.2. Припущення класичної лінійної моделі регресії в матричній формі
- •Припущення класичної лінійної моделі регресії
- •9.3. Оцінювання за мнк
- •9.4. Коефіцієнт детермінації r2 у матричному позначенні
- •9.5. Кореляційна матриця
- •9.6. Перевірка гіпотез про індивідуальні коефіцієнти регресії в матричному позначенні
- •9.7. Загальна перевірка регресії на значущість. Аналіз дисперсії в матричному позначенні
- •Матричне формулювання anova-таблиці
- •9.8. Перевірка лінійних обмежень. Загальний f-тест у матричних позначеннях
- •9.9. Прогнозування в множинній регресії. Матричне формулювання
- •9.10. Ілюстративний приклад у матричних позначеннях
- •Витрати на споживання на душу населення (ppce) і дохід на душу населення (ppdi) в сша за 1956–1970 рр.
- •Anova-таблиця для даних з таблиці 9.4.
3.10. Форма звіту за результатами регресійного аналізу
Існують різні форми звіту за результатами регресійного аналізу, але тут ми застосуємо ту, що належить до нашого ілюстрованого прикладу:
= (6,4138) (0,0357) = 0,9621 t = (3,8128) (14,2405) df = 8 5/11/1)
p
= (0,002571)
(0,000000289)
|
(3.10.1) |
У виразах (3.10.1) числа в дужках у другому рядку являють собою стандартні помилки коефіцієнтів регресії, числа в дужках у третьому рядку оцінки величин t:
|
|
у
припущенні нульової гіпотези про те,
що 1=0
і
2=0
(3,8128 = 24,4545/6,4138; 14,2405 = 0,5091/0,0357), а числа у
третьому рядку
обчислена ймовірність. Так, для 8 df
імовірність отримання величини
![]() дорівнює 0,0026, а ймовірність отримання
дорівнює 0,0026, а ймовірність отримання
![]()
близько 0,0000003.
близько 0,0000003.
Шляхом
подання імовірності р
оцінюваних коефіцієнтів ми можемо
відразу бачити точний рівень значимості
кожної оцінюваної величини t.
Так, при нульовій гіпотезі Н0:
1
= 0, точна імовірність (тобто величина
р)
отримання величини
приблизно дорівнює 0,0026. Отже, якщо ми
відкидаємо цю нульову гіпотезу,
імовірність того, що ми допускаємо
помилку 1
становить
26 випадків із 10 000, що насправді дуже
мало. У практичних задачах можна сказати,
що істинне значення
![]() .
Ще більше це стосується схильності до
покупки 2.
.
Ще більше це стосується схильності до
покупки 2.
Як
ми раніше згадували
![]() .
При нульовій гіпотезі
величина F=202,87
(1 df
чисельник, 8 df
знаменник), а t=14,24
(8
df);
відповідно до теорії (14,24)2=202,87.
.
При нульовій гіпотезі
величина F=202,87
(1 df
чисельник, 8 df
знаменник), а t=14,24
(8
df);
відповідно до теорії (14,24)2=202,87.
3.11. Обчислення результатів регресійного аналізу
У вступі нами була описана загальна схема економетричного моделювання:
Економічна теорія.
Математична модель теорії.
Економетрична модель теорії.
Дані.
Проведення оцінки параметрів економетричної моделі.
Перевірка гіпотез.
Прогнозування.
Використання моделі для прийняття рішень або з політичною метою.
Зараз, після подання результатів регресійного аналізу нашої моделі “споживання дохід” у вигляді (3.11.1), природно задати питання про адекватність цієї моделі. Наскільки «добре» вона підігнана до наявних даних? Для відповіді на це запитання нам потрібні деякі критерії.
По-перше,
чи відповідають знаки оцінених
коефіцієнтів теоретичним прогнозам
або наявному досвіду? Апріорі
,
схильність до покупки, повинна бути
позитивною. По-друге, якщо згідно з
теорією взаємозв’язок
повинен бути не тільки позитивним, але
й статистично значимим, чи виконується
це? Як ми зазначили в розд. 3, МРС –
схильність до покупки
є не тільки позитивною величиною, а й
статистично значимо відрізняється від
нуля. Ці ж зауваження стосуються й
коефіцієнта
.
По-третє, наскільки добре регресійна
модель пояснює зміну споживацьких
витрат? Для відповіді на це запитання
можна застосувати
.
У нашому випадку
![]() дуже високий, враховуючи, що максимальне
значення
є 1.
дуже високий, враховуючи, що максимальне
значення
є 1.
Таким
чином, вибрана нами модель для пояснення
характеру споживацьких витрат є цілком
прийнятною. Але перш ніж підвести межу,
цікаво з'ясувати, чи задовольнить модель
припущення CNLRM (classical normal linear regression model)
класичної лінійної моделі з нормальним
законом розподілу. Ми не звертатимемо
увагу на різні припущення, оскільки
модель є дуже простою. Але є одна гіпотеза,
яку ми хотіли б перевірити, а саме –
гіпотеза про нормальний розподіл
випадкової складової
![]() .
.
Пригадаємо, що використані раніше t- і F-тести припускали, що розподілена за нормальним законом розподілу. Інакше процедура перевірки не буде дійсна для малих або кінцевих вибірок.
Тест на нормальність
Хоча в літературі обговорюється ряд тестів перевірки на нормальність, обмежимося розглядом двох: 1) тест якості підгонки і 2) тест Jarque-Bera. Обидва ці тести використовують залишки і розподіл імовірності .
![]() тест
якості підгонки.
Цей тест проводять таким чином. Спочатку
ми отримуємо рівняння регресії, а також
залишки
,
підраховуємо стандартне відхилення
((
тест
якості підгонки.
Цей тест проводять таким чином. Спочатку
ми отримуємо рівняння регресії, а також
залишки
,
підраховуємо стандартне відхилення
((![]() ,
оскільки
).
Потім упорядковуємо залишки і розміщуємо
їх у різних групах (у нашому прикладі
ми розміщуємо їх у шести групах),
відповідних величині відхилення від
нуля. Для нашого прикладу ми одержуємо
такі дані (табл. 3.5).
,
оскільки
).
Потім упорядковуємо залишки і розміщуємо
їх у різних групах (у нашому прикладі
ми розміщуємо їх у шести групах),
відповідних величині відхилення від
нуля. Для нашого прикладу ми одержуємо
такі дані (табл. 3.5).
Таблиця 3.5

 ,
,