И нвертирующий упт

Коэффициент усиления где K, R₁ = R_вх и R_г считаются заданными.

Для уменьшения влияния среднего входного тока I_вх ОУ необходимо обеспечить равенство сопротивлений

в цепях инвертирующего и неинвертирующего входов, по которым протекают входные токи I_вх ОУ.

В цепи инвертирующего входа эквивалентное сопротивление равно .

В цепи неинвертирующего входа эквивалентное сопротивление находится из выражения:

,

которое получено исходя из того, что баланс ОУ (U_сдв=0) будет достигнут при почти среднем положении подвижного контакта потенциометра R₅. Если и потенциометр находится в среднем положении, то на его подвижном контакте напряжение будет равно нулю относительно общей шины ±U_п1,2.

Принимая R₄ = R₆, последнее выражение можно упростить:

Итак, и

Через делитель напряжения R₄, R₅, R₆ протекает сквозной ток I_дел = 2U_п / (R₄+R₅+R₆), или при R₄ = R₆

Максимальное напряжение, которое можно снять с делителя напряжения R₄, R₅, R₆ определяется выражением:

Далее оценим возможное максимальное напряжение сдвига выходного напряжения ОУ (без балансировки).

Чтобы компенсировать этот сдвиг, с делителя напряжения R₄, R₅, R₆ необходимо в цепь неинвертирующего входа ОУ подать напряжение U_{вых.дел}, равное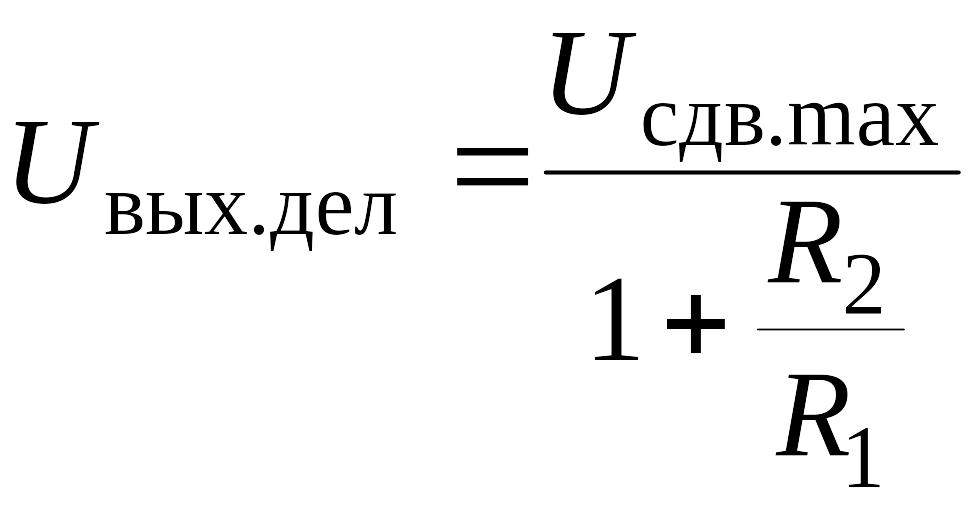 . Таким образом, мы получили шесть выражений, в которых четыре неизвестных: R₂, R₃, R₄ = R₆, R₅.

Г енератор треугольного напряжения

Классическая схема ГТН

Рассмотрим случай, когда U_см=0 (соответствующие клеммы замкнуты).

Интегратор на ОУ DА2 интегрирует выходное напряжение ±U₀ порогового устройства на ОУ DА1.

Значения ±U₀ стабилизированы стабилитронами VD1 и VD2, включенными последовательно и встречно.

; .

Если стабилитроны VD1 и VD2 идентичны (выбраны из одной и той же упаковки) или вместо них

применен двуханодный стабилитрон, то можно утверждать, что |–U₀| =U₀.

В схеме действует положительная обратная связь, поэтому она работает в автоколебательном двухтактном режиме.

В первом такте интегрируется напряжение, например, +U₀ до момента срабатывания порогового устройства на ОУ DА1,

и начинается процесс релаксации – интегрируется напряжение –U₀, происходит разинтегрирование опять до момента

срабатывания порогового устройства. Все это хорошо видно на диаграммах напряжения U₀(t) и U_вых(t).

Известно, что пороги срабатывания порогового устройства равны U₀R₁/R₂ и –U₀R₁/R₂.

Переключение режимов интегрирования происходит в моменты времени, когда –U_инт=U₀R₁/R₂ и U_инт= –U₀R₁/R₂ или,

так как U_инт(t) =U_вых(t), в моменты времени, когда –U_вых.m= U₀R₁/R₂ и U_вых.m= –U₀R₁/R₂.

Процессы интегрирования и разинтегрирования описываются уравнениями:

решая которые относительно Т₁ и Т₂, получаем где τ_и=R₅С₁– постоянная времени интегратора.

Частота следования треугольных импульсов

Итак,на выходе интегратора получили симметричное треугольное напряжение с полным размахом напряжения 2U₀R₁/R₂.Важно,что частота автоколебаний не зависит от U₀

ГТН со смещением выходного напряжения получается, если U_см≠0

Рассмотрим частный случай, когда .

Полный размах треугольного напряжения .

Решив уравнения, получим: и .

Частота следования треугольных импульсов будет равна

где τ_и=R₅С₁. Как видно, частота треугольного напряжения не зависит ни от напряжения смещения U_см, ни от опорного уровня U₀. Это весьма примечательно для практического использования ГТН