Вопрос№15. Определение термодинамической функции

Все расчеты в термодинамике основываются на ис­пользовании функций состояния, называемых термодинамическими функциями. Каждому наборунезависимых параметров соответствует своя термодина­мическая функция. Изменения функций, происхо­дящие в ходе каких-либо процессов, определяют либо со­вершаемую системой работу, либо получаемую системой теплоту. Термодинамические функции являются функциями состояния. Поэтому приращение любой из функции равно полному дифференциалу функции, которой она вы­ражается. 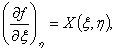Полный дифференциал функции f(x,у) пере­менных х и у определяется выражением         (1) Поэтому, если в ходе преобразований мы получим для при­ращёния некоторой величины f выражение вида      (2) можно утверждать, что эта величина является функцией параметров   и , причем функции  и  пред­ставляют собой частные производные функции :   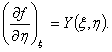     (3) При рассмотрении термодинамических функций мы будем пользоваться неравенством Клаузиуса, представив его в виде        (4) Знак равенства относится к обратимым, знак неравенст­ва - к необратимым процессам.

Свобо́дная эне́ргия Гельмго́льца (или просто свобо́дная эне́ргия) — термодинамический потенциал, убыль которого в квазистатическомизотермическом процессе равна работе, совершённой системой над внешними телами.

Свободная энергия Гельмгольца для системы с постоянным числом частиц определяется так:

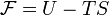• , где 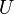  — внутренняя энергия, 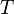  — абсолютная температура, 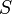  — энтропия.

Отсюда дифференциал свободной энергии равен:

• .

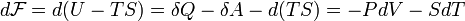Видно, что это выражение является полным дифференциалом относительно независимых переменных   и  . Поэтому часто свободную энергию Гельмгольца для равновесного состояния выражают как функцию  .

Для системы с переменным числом частиц дифференциал свободной энергии Гельмгольца записывается так:

• ,

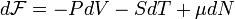где   — химический потенциал, а   — число частиц в системе. При этом свободная энергия Гельмгольца для равновесного состояния записывается как функция  .

В приложениях «свободной энергией» иногда называют не свободную энергию Гельмгольца, а энергию Гиббса. Это связано с тем, что энергия Гиббса также является мерой максимальной работы, но в данном случае рассматривается только работа над внешними телами, исключая среду:

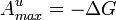• , где 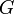  — энергия Гиббса.

• Электрохимический потенциал — физическая величина, связывающая химический потенциал (μ) и электрический потенциал (φ) некоторой электрохимической системы соотношением:

• A = μ + e·φ

• где А — работа, нарушающая электрохимическое равновесие системы; e — элементарный заряд частицы.

• Для растворенного вещества:

• μ = μ₀ + R*T*lnC + z*F*φ

• где

• μ₀ - Стандартный химический потенциал, зависящий от природы растворителя.

• С - концентрация вещества

• R - газовая постоянная

• T - температура

• z - валентность иона

• F - число Фарадея

• φ - электрический потенциал

  или   (1)  Уравнение (1) выражает первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил. Выражение (1) в дифференциальной форме будет иметь вид    или в более корректной форме   (2)  где dU — бесконечно малое изменение (приращение) внутренней энергии системы, δA — элементарная работа, δQ — бесконечно малое количество теплоты. В этом выражении dU является полным дифференциалом, а δA и δQ таковыми не являются. В дальнейшем будем использовать запись первого начала термодинамики в форме (2).  Из формулы (1) мы видим, что в СИ количество теплоты выражается в тех же единицах, что работа и энергия, т. е. в джоулях (Дж).  Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии равно нулю: ΔU=0. Тогда, согласно первому началу термодинамики,    т. е. вечный двигатель первого рода — периодически действующий двигатель, совершающий бoльшую работу, чем сообщенная ему извне энергия, — невозможен (одна из формулировок первого начала термодинамики).