34. Первая теорема двойственности.

Теорема: если одна из двойственных задач имеет оптимальный план, то и другая решима, т.е. имеет опт.план. При этом экстремальные значен.целевых функций совпадают (j=от 1 до n) Σcjxj*= (i=от 1 до m)Σbiyi* если в исходн. задаче целевая функция неограниченна на множестве планов, то в двойственной задаче система ограничений несовместна.

35. Вторая теорема двойственности и ее эконом.Интерпритация.

Для того, чтобы допустимые решения пары двойственных задач были оптимальными, необходимо и достаточно выполнение условия: xj*(∑aij yi*-cj)=0, j от 1 до n, yi*(∑aij xj*-bi)=0, I от 1 до m. Это условия дополняющей нежесткости. Из них следует: если какое-либо ограничение двойств.задачи обращ-ся оптималь.планом в строгое равенство, то соответствующая компонента опт. плана двойственной задачи должно равняться нулю.Если же какая-то компонента опт. плана равна нулю, то соответствующее ограничение двойств.задачи обращается опт.планом в строгое равенство хj*>0 следовательно (i= от 1 до m)Σaij yi*=cj (затраты на пр-во продукции=цене) – Если продукция вошла в опт.план, то если затраты>цены, объем пр-ва=0 Σaij yi* >cj следовательно xj*=0

yi*>0 следовательно (j=от 1 до n) Σaij xj*=bi (рас-ды рес-ов =запас рес-ов).

(j=от 1 до n) Σaij xj* <bi следовательно yi*=0

Смысл теоремы сводится к следующему:

-если стоимост.оценка рес-ов расход-х на пр-во ед.прод-ии=цене, то этот вид прод-ии входит в оптим.план ;

-если затраты превышают цену, то прод-ию производить не следует;

- еслирасход рес-ов=запасу, то стоимост.оценка этого рес-са положительна. Такой рес-с наз-ся дефицитным. Наибелее дефицит.рес-с обладает наибольшей оценкой;

-если рес-с израсходован неполностью, то его стоимост.оценка = 0.

18.Третья теорема двойственности и ее эконом.Интерпритация.

Теорема (об оценках): двойственные оценки показывают приращение функции цели, вызванное малым изменением свободного члена, соотв.ограничения двойственной задачи.

yi*= Δf max /Δ bi i=1, m или yi*=(f max)’ bi

yi*= Δf max / Δ bi

Δ f max = Δbi yi*

если Δ bi=1, то Δf max = yi* следовательно стоимост.оценка рес-са показ-т, как изменится выручка, если кол-во рес-са увелич-ся на единицу.

36.Интервал устойчивости двойственных оценок.

Двойственные оценки справедливы в допустимом интервале устойчивости, к-рый для ресурса pl, l=1,m имеет вид [bl+Δbl ; bl+Δbl ] , где Δbl – нижний придел уменьшения соответствующего рес-са; Δbl – верхний предел увеличения.

Эти величины (придел измен-ия колич.рес-сов) опред-ся по матрице обратной к матрице коэф-тов ограничений.

По формулам dkl>0

dkl<0

20.Формулировка и математич.Модель трансп.Задачи(тз) по критерию стоимости. Особенности модели как злп.

У m поставщиков А1, А2, …, Аm имеется a1, a2, …,am единиц однородного груза, к-рый д.б.доставлен n потребителям В1, В2, …, Вn в количествах b1, b2,…,bn. Известна стоимость( ) доставки ед-цы груза из пункта Ai в пункт Bj (j=от 1 до m). Необходимо найти такой план транспорт-ки прод-ии при к-ром суммарные затраты минимальны. Обозначим ч/з xij объем перевозки груза из i-го пункта в j-ый (i=от 1 до m; j=от 1 до n). Тогда матрица и есть план транспортировки груза Удельные трансп.издержки запис-ся в форме матрицы С=[cij]m *n и наз-ся она матрицей тарифов.

Экономико-матем.модель ТЗ должна отражать все условия и цель задачи в математич.форме. Переменные xij(i=от 1 до m;j=от 1 до n) должны удовлетворять ограничениям по запасам, потребностям и условиям неотрицательности:

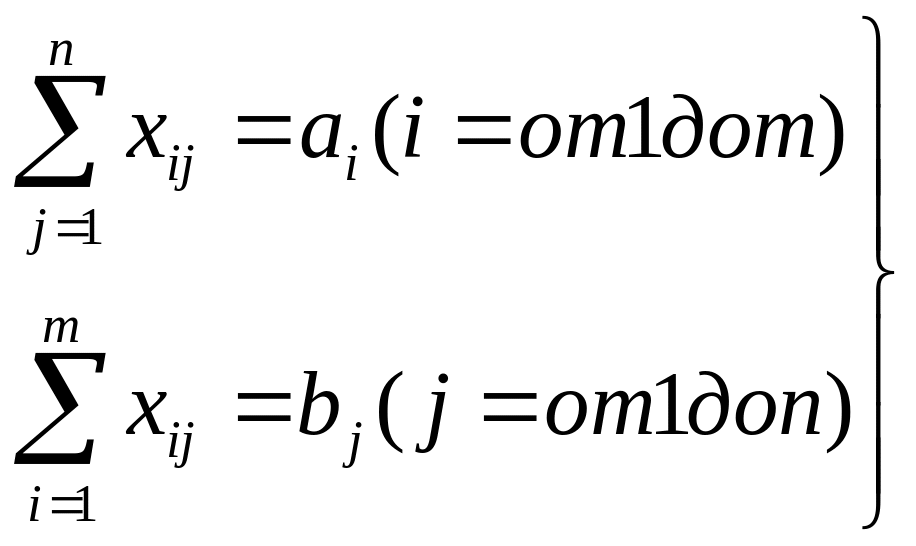(1)

xij>=0 (i=от 1 до m; j=от 1 до n) (2)

Цель ТЗ – минимизировать общие затраты на реализацию плана перевозок, к-рые можно представить функцией

f=c1.1 x1.1+c1.2 x1.2+…+c1.n x1.n+…+cm.1 xm.1+cm.2 xm.2+…+ cm.n xm.n =(i=от 1 до m)Σ(j=от 1 до n)Σcij xij. (3)

Математически ТЗ ставится так. Даны система ограничений (1) при условии (2) и линейная функция (3). Требуется среди множ-ва решений системы (1) найти такое неотрицат.решение, при к-ром линейная функция (3) принимает минимальное значение. План перевозок называется допустимым, если он удовлетворяет ограничениям (1) и (2). Допустимый план перевозок, доставляющий минимум целевой функции (3), наз-ся оптимальным.

Теорема: для того чтобы ТЗ имела допустимые планы, необходимо и достаточно выполнение равенства

(4)

Если равенство не выполняется, в задачу вводится фиктивный пославщик или потребитель.