20 Вопрос. Нормальный закон распределения.

В начале XIX века нормальное распределение затмило собой все остальные, поскольку в работах Гаусса и Лежандра утверждалось о нормальном законе распределения ошибок наблюдений. Нормальный закон распределения (или распределение Гаусса) задается следующей дифференциальной функцией параметры .

( - max = а - , x = а + - точки перегиба.

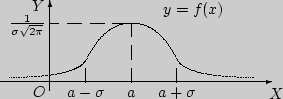
21.Характеристики нормального распределения случайной величины.

Непрерывная случайная величина называется распределённой по нормальному закону, если её плотность распределения вероятностей задается формулой: f(x)=1/(s*Ö2п) * е^-(х-мх)² / 2s² Наз. Законом Гаусса

Кривая Гаусса симметрична относительно прямой х=м_х

С в-ва кривой нормального распределения:

Если случайная величина х, представляет собой отклонение. Например: точки падения снаряда от точки прицеливания, то кривая f(х) будет характеризовать распределение точек падения снарядов по дальности. При этом центр рассеивания м_х будет характеризовать положение средней точки падения.

1. В точке х=м_х кривая имеет мах.=1/s*Ö2п

2. При êхꮥ ветви кривой асимптотически приближаются к оси 0х.

Замечание. Числовые характеристики.

1. M_{х =} m_{x =} ò_-¥ ^+¥ x*f(x)dx

2. D_x= ò_-¥ ^+¥ x²*f(x)dx

3. s_x =ÖD_x

22. Вероятность попадания значений случайной величины в заданный интервал. Функция Лапласа.

Вер-ть попадания нормально распределённой случайной величины в отрезке от[a;b]

P(a£x£b)=ò_a ^b f(x)dx=1/s*Ö2п* ò_a ^b е^-(х-м_x)² / 2s² dx

Определение. Интегралом вероятности наз-т функцию

Ф(х)= 1/Ö2п *ò₀ ^х е^-t2/2 dt

Замечание. Связь между Ф_х и Ф

Ф(х) =1/2 Ф(х/Ö2)

Св-ва функции Лапласа:

1. Ф(х)определяется на множестве R

2. Ф(0)=0

3. Ф(¥)=1

4. Ф(х) нечетная функция Ф(-х)= -Ф(х)

5. Ф(х) ­на (0;+¥)

6. График

P(a£x£b)=1/2[Ф(^b-мх/Ö2*s) – Ф(^a-мх/Ö2*s)]

Замечание. Вероятное отклонение и приведённая функция Лапласа

Определение. Вероятным отклонением случайной величины х, распределённой по нормальному закону наз.ся половина длины отрезка симметричного относительно центра рассеивания, вероятность попадания в который = 0.5

м_х+Е_х

ò f(x)dx=1/2 Е_х-Вероятное отклонение(кучность)

м_х+Е_х

Замечание. Обозначим Е_х /s_{х * Ö2 =} r r=0,477

Е_х= r*s_{х * Ö2 = 0,675*} s_х

Определение. Функция Лапласа Ф(х)= Ф(r_х)

P(a<x<b)=1/2[Ф(^b-мх/Ех) – Ф(^{a-мх/ÖЕх})]

23 Вопрос. Теорема трех сигм. Теорема Ляпунова

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм. Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D: Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа: Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее. На практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.

  Часто приходится иметь дело с такими случайными величинами, которые являются суммами большого числа независимых случайных величин. При некоторых весьма общих условиях оказывается, что эта сумма имеет распределение, близкое к нормальному, хотя каждое из слагаемых может не подчиняться нормальному закону распределения вероятностей. Эти условия были найдены Ляпуновым * и составляют содержание теоремы, названной его именем.    Приведем без доказательства только следствие из теоремы Ляпунова.    Пусть последовательность попарно независимых. случайных величин с математическими ожиданиями и дисперсиями , причем эти величины обладают следующими двумя свойствами:

  1) Cуществует такое число L, что для любого i имеет место неравенство , т, е. все значения случайных величин, как говорят, равномерно ограничены, относительно математических ожиданий;    2) Cумма неограниченно растет при .    Тогда при достаточно большом n сумма имеет распределение, близкое к нормальному.    Пусть a и - математическое ожидание и дисперсия случайной величины . Тогда 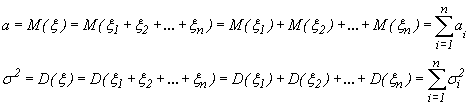   Так как по следствию из теоремы Ляпунова случайная величина для больших значений n имеет распределение, близкое к нормальному, то согласно формуле (32) имеет место соотношение

(56)

   где Ф(х) - интеграл вероятностей.