
- •1 Вопрос.
- •2 Вопрос
- •3 Вопрос. События и их виды.
- •5 Вопрос. Условная вероятность.
- •6 Вопрос. Формула полной вероятности.
- •7 Вопрос. Вероятность гипотез. Формула Байеса.
- •8 Вопрос. Последовательность независимых испытаний. Формула Бернулли.
- •9 Вопрос. Локальная теорема Лапласа. Интегральная теорема Лапласа.
- •10 Вопрос. Формула Пуассона.
- •11 Вопрос. Дискретная случайная величина. Ряд распределения.
- •12 Вопрос. Многоугольник распределения вероятностей.
- •13 Вопрос. Функция распределения, её свойства. Числовые характеристики распределения. Соединение из n элементов по m элементов.
- •14 Вопрос. Основные комбинаторные функции: размещения, постановка, сочетание.
- •15 Вопрос. Законы дискретных случайных величин и их числовые характеристики: биномиальное, Пуассона, геометрическое, гипергеометрическое.
- •16 Вопрос. Непрерывная случайная величина. Функция распределения. Плотность распределения.
- •17 Вопрос. Вероятность попадание случайной величины в заданный интервал.
- •18 Вопрос. Числовые характеристики случайной непрерывной величины.
- •19 Вопрос. Равномерный и показательный закон распределения.
- •20 Вопрос. Нормальный закон распределения.
- •21.Характеристики нормального распределения случайной величины.
- •22. Вероятность попадания значений случайной величины в заданный интервал. Функция Лапласа.
- •23 Вопрос. Теорема трех сигм. Теорема Ляпунова
- •24. Предмет математической статистики.
- •25 Вопрос. Генеральная совокупность.Выборка.
- •26 Вопрос. Вариационный ряд. Эмпирическая функция распределения. Гистограмма.
- •27 Вопрос. Точечные оценки параметров генеральной совокупности
- •30 Вопрос. Определение интервальной оценки. Интервальная оценка математического ожидания, среднего квадратического отклонения и вероятности.
- •31 Доверительные оценки.
- •32 Вопрос. Метод вычисление выборочных средних и дисперсий.
- •33 Вопрос. Понятие о системе случайных величин.
- •34 Вопрос. Постановка задачи теории корреляции
16 Вопрос. Непрерывная случайная величина. Функция распределения. Плотность распределения.
Определение 1. Непрерывной случайной величиной называют величина, которая в результате опыта может принимать любое значение из данного интервала
Замечание 1. Для непрерывной случайной величины нельзя заранее указать все ее возможные значения, так как она может принимать любое значение из данного интервала
Замечание 2. Закон распределение непрерывной случайной величины х удобно задавать с помощью функции распределения (плотности вероятности)
Определение
2. Вероятность,
того что значение R
в (![]() )
принятое
случайной величиной х попадет в отрезок
от aдо
b
определяется равенством
)
принятое
случайной величиной х попадет в отрезок
от aдо
b
определяется равенством ![]()
Замечание 3. график функции f(x) называется кривой распределения.
Свойства дифференцирования функции распределения
1.Функция
f(x)
![]() 0
0
2.![]()
3.
Все значения случайной величины x
заключены в промежутке от a
до b,
тогда последовательность равна ![]()
Замечание 4. Функция F(x) называют дифференциальной функцией распределения
Определение 3. Пусть функция распределения F(x) данной непрерывной случайной величины x непрерывна и дифференцируема всюду кроме может быть отдельных точек, тогда производная F(x) ее функция распределения называется плотностью распределения
Определение
4. Если
функция F(x)плотности
распределения вероятности непрерывной
случайной величины, тогда ![]()
17 Вопрос. Вероятность попадание случайной величины в заданный интервал.
Может быть вычислена двумя способами:
1)
через функцию распределения
![]()
2)
через плотность распределения
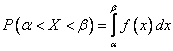
18 Вопрос. Числовые характеристики случайной непрерывной величины.
Определение
5. Математическим
ожиданием НСВ с плотностью вероятности
F(X)
называется число ![]()
Определение
6. Дисперсией
рассеивания случайной величины x
зазывается математическое ожидание
квадрата центрирования случайной
величины x0
и вычисляется ![]()
Определение 7. Центрированной случайной величиной икс с ноликом называется разность между случайной величиной x и ее математическим ожиданием.
Определение 8. В среднем квадрат отклонения случайной величины x называется квадратный корень из U дисперсией.
19 Вопрос. Равномерный и показательный закон распределения.
равномерный закон
Закон
равномерного распределения вероятностей
непрерывной случайной величины
используется при имитационном
моделировании сложных систем на ЭВМ
как первоначальная основа для получения
всех необходимых статистических
моделей. При этом, если специально не
оговорен закон распределения случайных
чисел, то имеют ввиду равномерное
распределение. Распределение вероятностей
называют равномерным, если на интервале
(a,b), которому принадлежат все возможные
значения случайной величины,
дифференциальная функция распределения
имеет постоянное значение, т. е. f(x) = C.
Так как
![]() то
то
![]() Отсюда
закон равномерного распределения
аналитически можно записать так:
Отсюда
закон равномерного распределения
аналитически можно записать так:
![]() График
дифференциальной функции равномерного
распределения вероятностей представлен
на рис. 6.5
График
дифференциальной функции равномерного
распределения вероятностей представлен
на рис. 6.5
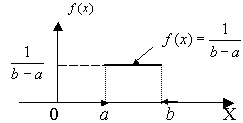 Рис.
6.5. Интегральную функцию равномерного
распределения аналитически можно
записать так:
Рис.
6.5. Интегральную функцию равномерного
распределения аналитически можно
записать так:
![]() График
интегральной функции равномерного
распределения вероятностей представлен
на рис. 6.6
График
интегральной функции равномерного
распределения вероятностей представлен
на рис. 6.6
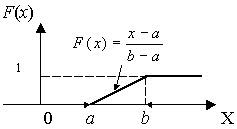
показательный закон
Непрерывная
случайная величина
![]() имеет
показательный закон распределения с
параметром
имеет
показательный закон распределения с
параметром
![]() ,
если ее плотность вероятности имеет
вид:
,
если ее плотность вероятности имеет
вид:
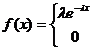
![]()
![]()
Функция распределения случайной величины , имеющей показательный закон распределения, равна:
![]()
![]()
ее математическое
ожидание
![]() ,
дисперсия:
,
дисперсия:
![]()
