5 Вопрос. Условная вероятность.

Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А.

Условной вероятностью (два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.

.

В частности, отсюда получаем .

6 Вопрос. Формула полной вероятности.

Пусть событие А может появиться вместе с одним из образующих полную группу попарнонесовместных событий Н₁,Н₂…Н_n называемых гипотезами, тогда вероятность события А вычисляется как сумма произведений вероятностей каждой гипотезы на вероятность события А при этой гипотезе

7 Вопрос. Вероятность гипотез. Формула Байеса.

Пусть событие А может наступить при условии появления одного из несовместных событий B₁, B₂,...,B_n образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности.

Пусть событие Н1…Нn образуют полную группу, тогда условная вероятность события Нi при условии, что событие А произошло определяется формулой Р(Нi/А)=Р(Нi)*Р(А/Нi)\Р(А) (теорема Байеса)

8 Вопрос. Последовательность независимых испытаний. Формула Бернулли.

Несколько опытов называются независимыми, если вероятность исхода каждого из опытов независит от того какие исходы имели другие опыты.

Теорема Бернулли.

Если производится n-независимых опытов в неизменных условиях, причина появление события А в каждом опыте равна вероятности, тогда вероятность не появления q=1-p, то вероятность того, что событие А появится равно m раз равна

9 Вопрос. Локальная теорема Лапласа. Интегральная теорема Лапласа.

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)

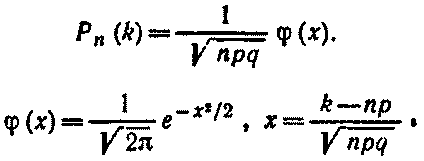
Для определения значений φ(x) можно воспользоваться специальной таблицей.

Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k₁ раз и не более k₂ раз, приближенно равна

P(k₁;k₂)=Φ(x'') - Φ(x')

Здесь

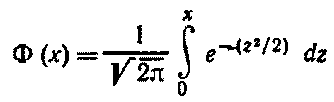
-функция Лапласа

Значения функции Лапласа находят по специальной таблице.