2.Спектри

Спектром сигналу називаються гармонічні (синусоїдальні) складові, якими подається цей сигнал. Якщо використати для подання періодичної функції формулу (1.3.1)

то звідти слідує, що спектр визначається сукупністю амплітуд косинусоїд , початкових фаз і частот .

Розподілення значень амплітуд гармонічних коливань по частоті зветься амплітудним спектром (або амплітудно-частотною характеристикою), а розподілення початкових фаз – фазовим спектром (або фазо-частотною характеристикою ).

Для багатьох практичних застосувань достатньо знати амплітудним спектр, тому коли кажуть спектр, то розуміють звичайно саме спектр амплітуд. В інших випадках роблять відповідні застереження.

Спектр періодичної функції має вигляд, показаний на Рис.1. Це дискретний спектр, який називається також лінійчастим (термін із оптики), або ще гармонічним.

Рис.1. Спектр періодичної функції

Це означає, що він складається з рівновіддалених (еквідистантних) спектральних ліній, які відповідають певним гармонікам, частоти котрих знаходяться у простих кратних співвідношеннях відносно основної (першої) гармоніки. Звичайно, окремі гармоніки, у тому числі і перша, можуть дорівнювати нулю. Дискретний спектр мають не тільки періодичні функції, а й неперіодичні, спектр яких складається із довільно розташованих на шкалі частот спектральних ліній і є вже не гармонічним

З поняттям рядів Фур’є тісно пов’язаний інтеграл Фур’є і перетворення Фур’є, коли останнє для дійсної функції , абсолютна величина якої інтегруєма на інтервалі , (тобто для якої існує інтеграл 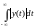) визначається так:

(1.4.1)

де називається комплексним спектром функції . Будучи комплексною функцією має дійсну та уявну частини, відповідно 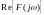та 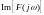, інакше кажучи, модуль та фазу . Формулу (1.4.1) ще називають прямим перетворенням Фур’є, оскільки безпосередньо (прямо) із функції часу отримується її спектр (амплітудний та фазовий). І навпаки, коли маємо той чи інший спектр, а бажано отримати їм відповідні часові функції, то використовується, так зване, обернене перетворення Фур’є, що задається наступним виразом:

3.Розрахункова частина роботи

Завдання 1

Дискретизований сигнал заданий своїми значеннями у наступній таблиці:

	0	1	2	3	4	5	6	7	8	9
	0	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6	1.8
	0.86	-0.71	0.08	-0.21	-0.47	-1.6	-0.51	1.35	4.21	10.8

Для проведення розрахунків скористаємось описаними нижче формулами. Для крайніх точок використаємо наступні дві формули:

Для решти точок використаємо наступну формулу:

Виведення даної формули наведено в коротких теоретичних відомостях (пункт 1 розрахункової роботи)

Розрахунок першого проходу:

Використаємо результати, отримані при першому проході обчислень для реалізації другого проходу:

Розрахуємо значення відхилень для першого проходу:

Розрахуємо значення відхилень для другого проходу:

Максимальні по модулю значення відхилень для обох проходів:

Знайдемо суму квадратів відхилень для першого і другого проходів:

Таблиці результатів та графіки наведенні у висновку.

Завдання 2

На основі аналізу виразу аналітичного сигналу і заданих його параметрів виконаємо наступні дії

, де -інтервал визначення сигналу,в нашому випадку

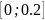
Тоді

В сигналі присутня постійна складова: А₁сиг=0.5.

Гармонічна складова для сталого сигналу має ненульову амплітуду,яка визначається Асп=А₁сиг*N=0.5*40=20 на частоті f₁=0 Гц і фазу φ₁=0.

Спектр даного сигналу подається з кроком дискретизації .

Розглянемо наступну складову: 1.2sin( )

A₂сиг=1.2. Гармонічна складова для додатної синусоїди має ненульову амплітуду, яка визначається Асп = А₂сиг *N/2=1.2*40/2=24 присутня на частоті f2=10 Гц з фазою φ₂=-90, f3=-10= з фазою φ₃=90 оскільки складова сигналу періодична то відбувається повтор на частоті 200-10=190.

Розглянемо наступну складову: 0.4sin( )

A₂сиг=0.4. Гармонічна складова для додатної синусоїди має ненульову амплітуду, яка визначається Асп = А₂сиг *N/2=0.4*40/2=8 присутня на частоті f4=40 Гц з фазою φ₄=-90, f5=-40= з фазою φ5=90 оскільки складова сигналу періодична то відбувається повтор на частоті 200-40=160.

Результати приведені в таблиці.