Міністерство освіти і науки України
Національний технічний університет України „КПІ”
Факультет інформатики і обчислювальної техніки
Кафедра технічної кібернетики
Розрахунково-графічна робота по курсу «Системи обробки сигналів та зображень»
Виконав студент Перевірив
ІІ курсу Ігнатенко В.М.
групи ІК-02
Ніколаєнко В.М.
Київ 2012
Зміст
Варіант індивідуального завдання
Короткі теоретичні відомості
Розрахункова частина роботи
Табличні та графічні результати розрахунково-графічної роботи.
1.Варіант індивідуального завдання
Варіант 4
4.1
Дискретизовний сигнал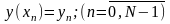 заданий своїми значеннями у наступній
таблиці:
заданий своїми значеннями у наступній
таблиці:
-
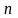
0
1
2
3
4
5
6
7
8
9

0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
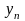
0.86
-0.71
0.08
-0.21
-0.47
-1.6
-0.51
1.35
4.21
10.8
Провести двократне згладжування поліномом першої степені по трьом точкам на кожному кроці згладжування. Вирахувати значення різниць (відхилень) між значеннями вихідних і згладжених даних, знайти максимальне по модулю значення їх різниці та суму квадратів відхилень між вихідними та згладженими даними. Подати усі вихідні дані та результати обчислювань у відповідній табличній та графічній (Взяти дані з файлу V121.xy)
4.2
Дискретизовний періодичний сигнал,який
має період дискретизації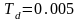 сек,
заданий на інтервалі
сек,
заданий на інтервалі
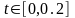 виразом
виразом
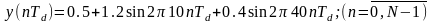 ,
де N-
число дискрет. Знайти
спектр сигналу (амплітудний
,
де N-
число дискрет. Знайти
спектр сигналу (амплітудний
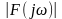 та фазовий
та фазовий
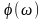 )
, подавши результати у вигляді
відповідних таблиць і графіків як
функції частоти.
)
, подавши результати у вигляді
відповідних таблиць і графіків як
функції частоти.
2.Короткі теоретичні відомості
Метод поліноміального згладжування
Метод ковзаючого
середнього має один суттєвий недолік
– зростаюча втрата даних при збільшені
числа проходів згладжування. Цей недолік
можна усунути якщо замість полінома
нулевої степені
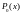 використати поліном першої степені
використати поліном першої степені
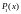 ,
який має вже два шуканих коефіцієнта
,
який має вже два шуканих коефіцієнта
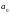 та
та
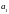 ;
тобто він подається у такому вигляді
;
тобто він подається у такому вигляді
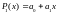 і задає пряму лінію. Знову ж таки вибираємо
дял побудови цього поліному мінімально
можливу кількість даних з вихідного
масиву
і задає пряму лінію. Знову ж таки вибираємо
дял побудови цього поліному мінімально
можливу кількість даних з вихідного
масиву
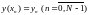 - три, записуючи квадратичну міру
близькості і поліном у такому вигляді:
- три, записуючи квадратичну міру
близькості і поліном у такому вигляді:
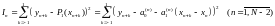 (2.2.7)
(2.2.7)
Оптимальні значення
шуканих коефіцієнтів
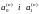 на
на
 -тому
кроці згладжування знаходиться із умови
екстремуму (мінімуму) міри близькості
(2.2.7), тобто:
-тому
кроці згладжування знаходиться із умови
екстремуму (мінімуму) міри близькості
(2.2.7), тобто:

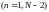 (2.2.8)
(2.2.8)
що дає після перетворення таку систему алгебраїчних рівнянь:
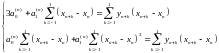 (2.2.9)
(2.2.9)
Припускаючи, що
дискрети
 рівновіддалені одна від одної з інтервалом
рівновіддалені одна від одної з інтервалом
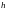 ,
маємо:
,
маємо:
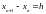
а в системі рівнянь (2.2.9) отримуємо такі коефіцієнти:

В результаті система рівнянь (2.2.9) перетворюється в таку:
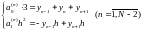 (2.2.10)
(2.2.10)
що дає наступний розв’язок:
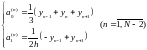 (2.2.11)
(2.2.11)
Оскільки значення
згладжених даних тепер розраховуються
по поліному
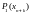 у точці
у точці
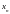 ,
то
,
то
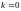 і у виразі
і у виразі
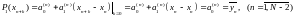 (2.2.12)
(2.2.12)
зникає різниця
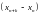 і тому залишається тільки
і тому залишається тільки
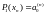 ,
тобто необхідно використати тільки
коефіцієнт
,
тобто необхідно використати тільки
коефіцієнт
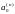 ,
,
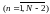 ,
а значить і вирахувати тільки наступне:
,
а значить і вирахувати тільки наступне:
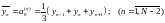 (2.2.13)
(2.2.13)
Якщо поставити
за мету не втрачати по два значення –
одне на початку, а друге – в кінці масиву
даних, то потрібно скористатися повним
виразом для поліному
з коефіцієнтами
при
 і
і
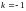 ,
а також
,
а також
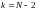 і
і
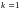 відповідно, що дає:
відповідно, що дає:

(2.2.14)
Підставивши (2.2.11) в (2.2.14) отримуємо таке: