
- •10 Инт. Вида ,
- •11 Инт. Вида
- •1 Кч в алгебраической форме
- •2 Тригонометрическая форма кч
- •3 Извлечение корня из кч
- •4 Основная теорема алгебры и ее следствия
- •2 Свойства инт.
- •6 Инт. По частям
- •7 Инт. Рациональных функций.
- •8 Инт. Иррациональных функций
- •8.2 Инт. Биномиальных дифференциалов
- •9 Инт. Тригон. Выражений
- •2. Dу1, решения которых сводится к интегралам
- •3. Сущ. И ед. Решения dу1.
- •2 Сущ. И ед. Решения.
- •2 Сущ. И ед. Решения нсdу
- •3 Метод исключения
2 Сущ. И ед. Решения нсdу
Пусть
1) все фун.![]() непр. в
, 2) все ЧП
непр. в
, 2) все ЧП
![]() ограничены
в Ω ,
ограничены
в Ω ,
тогда сущ. ед. решение ЗК с началом в любой т. из .
3 Метод исключения
Для определенности рассмотрим систему из 2-х уравнений
![]() ,
,
![]()
Берем
1-е уравн.
![]() и дифф. его
и дифф. его
![]() .
.
В результате получаем систему
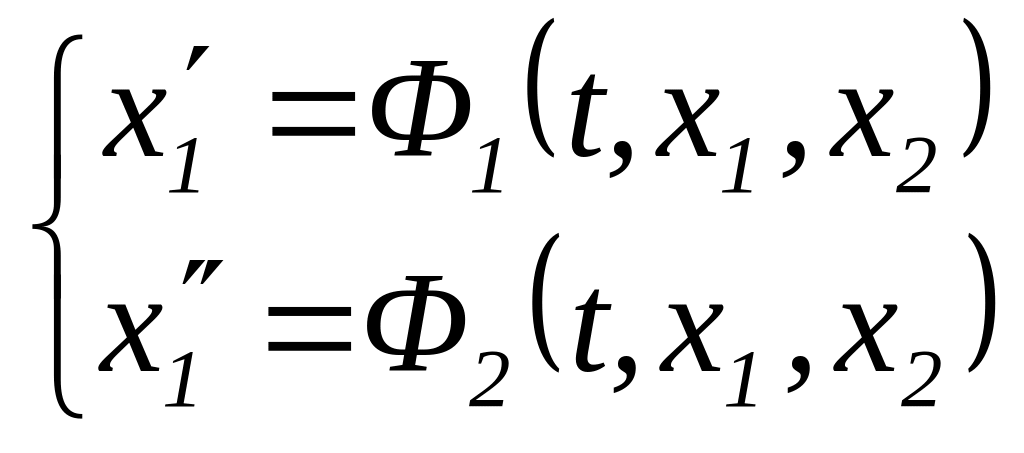
исключаем x2 и получаем DУ2 относительно x1 .
Пр.
![]()
Все! окончание 2-го семестра
****************************************************************************
1.Теорема. Пусть решения уравнения , набор лин. независимый .
допустим
что
![]() , тогда столбцы в
, тогда столбцы в
![]() лин. зав., т.е. сущ. числа
, не все =0 такие, что
лин. зав., т.е. сущ. числа
, не все =0 такие, что
![]() , рассмотрим решение
, рассмотрим решение
![]() ,по
теореме ед.
,по
теореме ед.
![]() ,
что противоречит лин. незав., все!
,
что противоречит лин. незав., все!
********************************************************************
DУ1,
неразрешенные относительно
![]() (схемы решений)
(схемы решений)
1.
![]()
Пусть
![]() −корень уравнения
−корень уравнения
![]() ,
тогда
,
тогда
![]() ,
,
![]() , а
, а
![]() −общий интеграл, все!
−общий интеграл, все!
2.
![]()
Пусть
![]() ,тогда
,тогда
![]() ,
найдем x:
,
найдем x:
![]() ,
,
![]() ,
,
![]() ; получили общий интеграл в парам. форме:
; получили общий интеграл в парам. форме:
![]() ,
все! Пр.
,
все! Пр.
![]() .
.
3.
![]() .
.
Пусть
![]() , тогда
, тогда
![]() ,
,
![]() ,
,
![]() ; общий интеграл:
; общий интеграл:
![]() ,
все! Пр.
,
все! Пр.
![]() .
.
4.
![]() . Пусть
,
тогда
. Пусть
,
тогда
![]() ,
,
![]() ,
,
получили
уравнение для x:
![]() ,
его решение
,
его решение
![]() вместе с
вместе с
дают решение исходного уравнения в парам. форме, все!
5.
![]() . Пусть
, тогда
. Пусть
, тогда
![]() ,
,
![]() ,
,
получили
уравнение для y:
![]() , его решение
, его решение
![]() вместе с
дает решение исходного уравнения, все!
вместе с
дает решение исходного уравнения, все!
Пр.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
*********************************************************************
