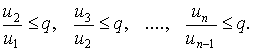Необходимый признак сходимости числового ряда.
Теорема: Пусть числовой ряд
u1+u2+...+un+... , |
(1) |
сходится, а S - его сумма. Тогда при неограниченном возрастании числа n членов ряда его общий член unстремится к нулю Доказательство. Из условия теоремы имеем
Так как
Sn - Sn-1 = un
то
Следует отметить, что этот признак является лишь необходимым, но не достаточным признаком сходимости ряда, так как можно указать ряд, для которого выполняется равенство
,
а он, однако не является сходящимся. Так гармонический ряд
,
для которого
,
расходится. Но согласно доказанному необходимому признаку сходимости ряда, если
,
то ряд (1) расходится. В самом деле, если бы он сходился, то
равнялся бы нулю. Таким образом, доказанная нами теорема иногда позволяет, не вычисляя суммы Sn, сделать заключение о расходимости того или иного ряда. Например, ряд
,
расходится, так как
,
39. Пусть дан ряд
u1+u2+u3+...+un+... , |
(1) |
с положительными членами. Относительно этого ряда имеют место две следующие теоремы Даламбера.
Теорема 1. Если отношение каждого последующего члена ряда (1) к предидущему члену меньше фиксированного числа q<1 (или равно q), то ряд (1) сходится; если это отношение больше 1 (или равно1), то ряд (1) расходится. Доказательство. 1. Пусть
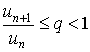
Тогда имеют место неравенства
|
(2) |
Отсюда
|
(3) |
или
|
(4) |
Складывая почленно неравенства (4), получим неравенство
|
(5) |
Но
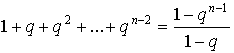
а поэтому
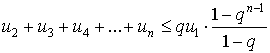
По условию теоремы, q<1 , а поэтому
Следовательно,
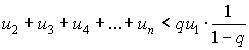
при любом n. Прибавляя u1 к обеим частям последнего неравенства, получим
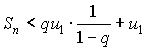
или
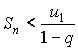
Так как все члены ряда (1) положительны и, следовательно, Sn с возрастанием n возрастает, оставаясь меньше
то существует предел Sn и
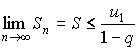
Таким образом ряд (1) сходится. 2. Теперь пусть
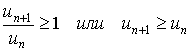
Это означает, что с возрастанием n общий член un ряда (1) не убывает, т.е. не выполняется необходимый признак сходимости ряда, а поэтому ряд (1) расходится.
Теорема 2. Пусть l - предел отношения последующего члена un+1 ряда (1) к предидущему un при n®Ґ, т.е.
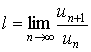
Тогда, если l < 1, то ряд l сходится, если l > 1, то ряд l расходится, Если же l = 1, то вопрос о сходимости ряда (1) остается открытым. Доказательство. Согласно определению предела переменной величины, равенство
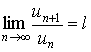
означает, что, начиная с некоторого номера n, выполняются неравенства
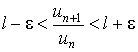
где e - наперед заданное сколь угодно малое положительное число. Рассмотрим три случая: а) пусть l < 1 . Тогда всегда можно взять e настолько малым, чтобы выполнялось неравенство
l + e < 1
и, начиная с некоторого n , неравенство
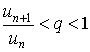
где q = l + e , в силу чего ряд (1) будет сходящимся; б) пусть l > 1 . Выбираем e так, чтобы
e = l - 1 > 0
Тогда l - e = 1 и
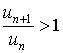
т.е. ряд (1) расходится в) пусть l = 1 . Тогда ряд (1) может быть как сходящимся, так и расходящимся. В самом деле, для гармонического ряда
который расходится, имеем,
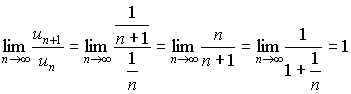
С другой стороны, ряд
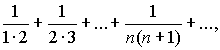
сходится, а для него также
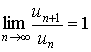
потому что
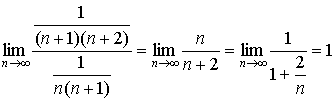
Таким образом, доказано, что если
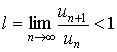
то ряд (1) сходится; если l > 1 , то ряд (1) расходится. Теорема 2 выражает признак Даламбера.
40.
Рассмотрим положительный
числовой ряд 
.
Если существует предел: 
,
то:
а)
При D<1 ряд сходится.
В частности, ряд сходится при D=0.
б)
При D>1 ряд расходится.
В частности, ряд расходится при 
.
в)
При D=1
признак
не дает ответа.
Нужно использовать другой признак.
Интересно отметить, что если признак
Коши не даёт нам ответа на вопрос о
сходимости ряда, то признак Даламбера
нам тоже не даст ответа. Но если признак
Даламбера не даёт ответа, то признак
Коши вполне может «сработать». То есть,
признак Коши является в этом смысле
более сильным признаком.