26. Дифференциальные уравнения с разделяющимися переменными

(3.1)

называется уравнением с разделяющимися переменными.

Умножая обе части уравнения на , получаем уравнение (3.2)

В уравнении (3.2) коэффициент при dx зависит только от x, а коэффициент при dy зависит только от y. Значит, в уравнении (3.2) переменные разделены. Интегрируя, получаем:

.

27.Однородные диф. Уравнения и приводящиеся к ним

К однородным уравнениям первого порядка приводится уравнение вида:

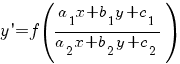
Как определить, что дифференциальное уравнение приводится к однородному

Для того, чтобы определить, что дифференциальное уравнение приводится к однородному, нужно выделить две линейные формы:

a1 x + b1 y + c1, a2 x + b2 y + c2, и выполнить замену:

a1 x + b1 y + c1 → t(a1 x + b1 y + c1);

a2 x + b2 y + c2 → t(a2 x + b2 y + c2)

Если после преобразований t сократится, то это уравнение приводится к однородному.

Пример

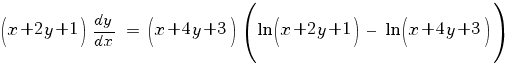
Выделяем две линейные формы:

x+2y+1 и x+4y+3.

Первую заменим на t(x+2y+1), вторую - на t(x+4y+3):

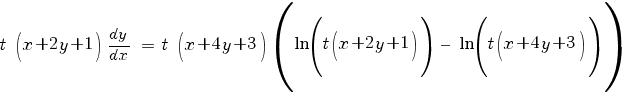
По свойству логарифма:

t сокращается:

Значит это уравнение приводится к однородным.

Решение дифференциального уравнения, приводящегося к однородному уравнению

Решаем систему уравнений:

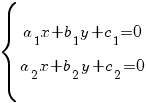
Здесь возможны три случая:

1) Система имеет бесконечное множество решений (прямые a1 x + b1 y + c1 = 0 и a2 x + b2 y + c2 = 0 совпадают). В этом случае

Тогда

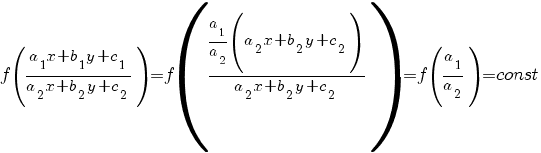
Это простейший вид уравнения с разделяющимися переменными:

Его решение:

2) Система не имеет решений (прямые a1 x + b1 y + c1 = 0 и a2 x + b2 y + c2 = 0 параллельны). В этом случае a1 b2 – a2 b1 = 0;

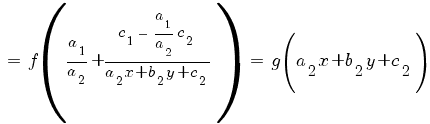
Это уравнение приводится к уравнению с разделяющимися переменными подстановкой

z = a2 x + b2 y + c2.

3) Система имеет одно решение (прямые a1 x + b1 y + c1 = 0 и a2 x + b2 y + c2 = 0 пересекаются в одной точке). Обозначим это решение x0, y0. Тогда

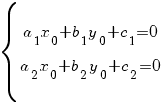
Делаем подстановку x = t + x0, y = u + y0. Тогда dx = dt, dy = du,

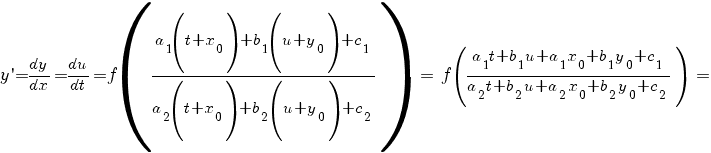
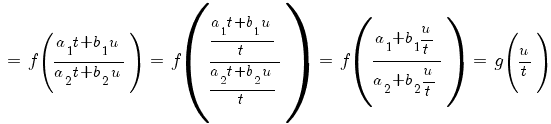
Или

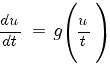
28.Уравнения в полных дифференциалах

(1)

называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции , т.е.

Теорема.

Если функции непрерывны в некоторой односвязной области , то условие

является необходимым и достаточным для того, чтобы выражение

, было полным дифференциалом функции .

Если известна функция, полным дифференциалом которой является левая часть уравнения (1), то все решения этого уравнения имеют вид , где - произвольная постоянная.

Чтобы найти функцию нужно воспользоваться равенствами

(2)

Интегрируя первое из этих равенств по x, определим функцию с точностью до произвольной дифференцируемой функции переменного y:

(3)

где - произвольная дифференцируемая функция. Функция , такая что . Дифференцируя (3) по y, с учетом второго равенства из (2) получаем уравнение для определения :

.