
- •22.Производная по направлению.Градиент
- •23.Ротор (вихрь) векторного поля
- •24. Оператор Гамильтона и его применение
- •25.Дифференциальные уравнения. Порядок, решение, общий интеграл.
- •26. Дифференциальные уравнения с разделяющимися переменными
- •27.Однородные диф. Уравнения и приводящиеся к ним
- •28.Уравнения в полных дифференциалах
- •29.Линейные уравнения 1-го порядка и методы их решения
- •30. Уравнения, допускающие понижение порядка.
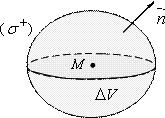
2![]() 1.Дивиргенция
(или расходимость) векторного поля
1.Дивиргенция
(или расходимость) векторного поля![]() в точке
в точке![]() — это предел отношения потока вектора
— это предел отношения потока вектора
![]() через
замкнутую поверхность
через
замкнутую поверхность![]() , окружающую точку
,
в направлении ее внешней нормали к
объему, ограниченному этой поверхностью,
при условии, что вся поверхность
стягивается в точку
(1)
, окружающую точку
,
в направлении ее внешней нормали к
объему, ограниченному этой поверхностью,
при условии, что вся поверхность
стягивается в точку
(1)
Þ![]() — дивергенция является производной
потока через замкнутую ориентированную
поверхность по объёму, ограниченному
этой поверхностью.
— дивергенция является производной
потока через замкнутую ориентированную
поверхность по объёму, ограниченному
этой поверхностью.
Основные свойства дивергенции
1. — это дифференциальная характеристика поля, является скалярной величиной.
2.
В каждой точке![]() поля
поля![]() показывает наличие источников или
стоков поля:
показывает наличие источников или
стоков поля:
§
если![]() , то в точке
есть источник поля
,
при этом значение
, то в точке
есть источник поля
,
при этом значение
![]() численно равно мощности источника;
численно равно мощности источника;
§
если
![]() ,
то в точке
есть сток поля
,
при этом значение
,
то в точке
есть сток поля
,
при этом значение
![]() численно равно мощности стока;
численно равно мощности стока;
§
если
![]() ,
то в точке
нет ни источника, ни стока поля
.
,
то в точке
нет ни источника, ни стока поля
.
3.
![]() вычисляется
по формуле:
вычисляется
по формуле:
![]() (2)
(2)
Воспользуемся формулой Остроградского—Гаусса, связывающей интеграл по замкнутой поверхности с интегралом по объёму, ограниченному этой поверхностью:
![]()
Применяем теорему о среднем к тройному интегралу:
![]()
где М1 — это некоторая фиксированная точка в объёме, ограниченном замкнутой поверхностью (σ),
 —величина этого объёма.
—величина этого объёма.
Теперь используем определение (1) дивергенции:
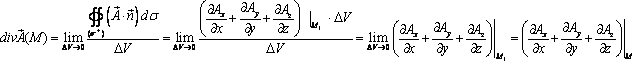
так
как при![]() точка M1стремится к точке
M.
точка M1стремится к точке
M.
4. Если использовать понятие дивергенции, то теорема Остроградского-Гаусса в векторной форме:
(3)
![]()
то
есть поток вектора
изнутри замкнутой поверхности
![]() равен тройному интегралу от дивергенции
вектора
по объему, ограниченному этой поверхностью.
равен тройному интегралу от дивергенции
вектора
по объему, ограниченному этой поверхностью.
Так
как
![]() можно рассматривать как плотность
распределения источников и стоков
векторного поля
,
то тройной интеграл
можно рассматривать как плотность
распределения источников и стоков
векторного поля
,
то тройной интеграл
![]() равен суммарной мощности источников и
стоков по объему
равен суммарной мощности источников и
стоков по объему
![]() .
.
Учитывая это, смысл теоремы Остроградского-Гаусса в форме (3) можно сформулировать следующим образом:
поток векторного поля изнутри замкнутой поверхности равен суммарной мощности источников и стоков этого поля, заключенных в объеме , ограниченном этой поверхностью .
Следовательно, если поток равен 0, то внутри поверхности нет источников и стоков поля или они уравновешивают друг друга.
5. Линейность дивергенции:
![]()
Это следует из линейности операций сложения векторов и дифференцирования.
6.
Дивергенция прозведения скалярного
поля
![]() на векторное поле
на векторное поле
![]() вычисляется по формуле:
вычисляется по формуле:
![]()
![]()
![]()
![]()
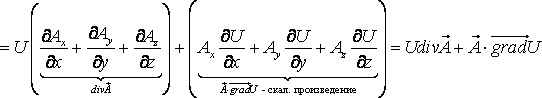
22.Производная по направлению.Градиент
Пусть
снова функция
![]() задана в области
задана в области
![]() и имеет во всех точках
и имеет во всех точках
![]() частные производные по всем переменным
частные производные по всем переменным
![]() . Предположим, что все частные производные
. Предположим, что все частные производные
![]() непрерывны в точке
непрерывны в точке
![]() . Тогда функция
дифференцируема в точке
. Тогда функция
дифференцируема в точке
![]() , то есть приращение функции
, то есть приращение функции
![]() имеет главную линейную часть, которая
равна дифференциалу:
имеет главную линейную часть, которая
равна дифференциалу:
![]()
где
![]() -- величина большего порядка малости
при
-- величина большего порядка малости
при
![]() , чем
, чем
![]() . Напомним, что
. Напомним, что
![]()
так что получаем
![]()
Фиксируем
теперь в
![]() какое-нибудь направление, выбрав задающий
его ненулевой вектор
какое-нибудь направление, выбрав задающий
его ненулевой вектор
![]() Через точку
в направлении вектора
Через точку
в направлении вектора
![]() проходит некоторая ось
проходит некоторая ось
![]() . (Напомним, что осью называется прямая
с выбранным на ней направлением, то есть
выбранным порядком следования точек.)
Точки
. (Напомним, что осью называется прямая
с выбранным на ней направлением, то есть
выбранным порядком следования точек.)
Точки
![]() этой оси можно задать параметрическими
уравнениями:
этой оси можно задать параметрическими
уравнениями:
![]()
или,
в векторном виде,
![]() , где
, где
![]() и увеличению значений параметра
и увеличению значений параметра
![]() соответствует
движение точки
соответствует
движение точки
![]() оси в направлении вектора
.
оси в направлении вектора
.
Обозначим
![]() ту часть оси
, которая состоит из точек оси, следующих
после
,
то есть точек луча
ту часть оси
, которая состоит из точек оси, следующих
после
,
то есть точек луча
![]() ,
получающегося при
,
получающегося при
![]() .
.
Градент
Для
случая трёхмерного пространства
градиентом скалярной функции
![]() координат xyz называется
векторная функция с компонентами
координат xyz называется
векторная функция с компонентами
![]()
![]()
![]()
Или,
использовав для единичных векторов по
осям прямоугольных декартовых координат
![]() :
:
Если
![]() — функция переменных
— функция переменных![]() , то её градиентом называется n-мерный
вектор
, то её градиентом называется n-мерный
вектор
![]()
компоненты которого равны частным производным по всем её аргументам.
Размерность
вектора градиента определяется, таким
образом, размерностью пространства
(или многообразия), на котором задано
скалярное поле, о градиенте которого
идет речь.Оператором градиента
(обозначаемым обычно, как говорилось
выше,
![]() или
или
![]() )
называется оператор, действие которого
на скалярную функцию (поле) дает ее
градиент. Этот оператор иногда коротко
называют просто «градиентом».Смысл
градиента любой скалярной функции в
том, что его скалярное произведение с
бесконечно малым вектором перемещения
)
называется оператор, действие которого
на скалярную функцию (поле) дает ее
градиент. Этот оператор иногда коротко
называют просто «градиентом».Смысл
градиента любой скалярной функции в
том, что его скалярное произведение с
бесконечно малым вектором перемещения
![]() дает полный дифференциал этой функции
при соответствующем изменении координат
в пространстве, на котором определена
дает полный дифференциал этой функции
при соответствующем изменении координат
в пространстве, на котором определена
![]() ,
то есть линейную (в случае общего
положения она же главная) часть изменения
при смещении на
.
Применяя одну и ту же букву для обозначения
функции от вектора и соответствующей
функции от его координат, можно написать:
,
то есть линейную (в случае общего
положения она же главная) часть изменения
при смещении на
.
Применяя одну и ту же букву для обозначения
функции от вектора и соответствующей
функции от его координат, можно написать:
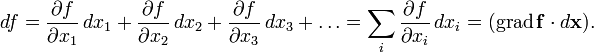
Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат , то есть от природы параметров x вообще, то полученный дифференциал является инвариантом, то есть скаляром, при любых преобразованиях координат, а поскольку — это вектор, то градиент, вычисленный обычным образом, оказывается ковариантным вектором, то есть вектором, представленным в дуальном базисе, какой только и может дать скаляр при простом суммировании произведений координат обычного (контравариантного), то есть вектором, записанным в обычном базисе. Таким образом, выражение (вообще говоря — для произвольных криволинейных координат) может быть вполне правильно и инвариантно записано как:
![]()
или, опуская по правилу Эйнштейна знак суммы,
![]()
(в ортонормированном базисе мы можем писать все индексы нижними, как мы и делали выше). Однако градиент оказывается настоящим ковариантным вектором в любых криволинейных координатах.
