19. Угловая невязка и её распределение в замкнутом теодолитном ходе.

Определение угловой невязки в замкнутом ходе по формуле:

где ∑β_П – сумма измеренных углов ; ∑β_т – теоретическая сумма углов, при этом ∑β_теор=180(n-2) –сумма внутренних углов замкнутого многоугольника (n-число сторон).

Подсчитать допустимую угловую невязку хода по формуле:

где n- число углов в ходе.

При соблюдении условия угловую невязку необходимо распределить с обратным знаком на все углы поровну с округлением до 1

-поправка на угол.

Контроль вычисления поправок:=

Контролем правильности вычислений служит равенство:

19. Вычисление дирекционного угла последующей стороны теодолитного хода.

Дирекционный угол α – это угол, отсчитываемый от северного направления осевого меридиана или линии параллельной ему до данного направления по ходу часовой стрелки. Дирекционные углы могут изменяться от 0° до 360° . Исходный угол стороны γ-1 задан, дирекционные углы последующих сторон вычисляются по формуле:

19. Вычисление приращений и координат замкнутого теодолитного хода. Контроли.

Вычисление приращений координат ∆X и ∆Y по дирекционным углам и горизонтальным проложениям сторон теодолитного хода по формулам:

где - горизонтальное проложение стороны хода,- дирекционный угол, соответствующий данному направлению

Знаки приращений определить в зависимости от дирекционных углов.

Вычисление невязок приращений

Невязки приращений координат – это разности их вычисленного и теоретического значения

_∆X=∑∆X_выч-∑∆X_{теор ∆Y}=∑∆Y_выч-∑∆Y_теор

Так как ход замкнут, то теоретические суммы приращений координат ∑∆X_теор=0 ∑∆Y_теор=0

Невязки приращений координат будут равны вычисленным суммам приращений координат

_∆X=∑∆X_выч

_∆Y=∑∆Y_выч

Далее необходимо вычислить абсолютную и относительную невязку /P и сравнить с допустимой невязкой, P- длина хода.

Следующим шагом является распределение невязок _∆X ,_∆Y на каждое приращение с обратным знаком пропорционально длине линии. После этого нужно вычислить исправленные значения приращений координат для каждой линии.

Контроль:=

∆X_{i испр}=∆X_{i выч}+

∆Y_{i испр}=∆Y_{i выч}+

Контроль:

Вычислить координаты X и Y , получая координаты каждой последующей вершины хода как алгебраическую сумму координат предыдущей вершины с соответствующим исправленным приращением

X_i+1 =X_i+∆X_{i испр}

Y_i+1 =Y_i+∆Y_{i испр}

Контроль получение исходных координат: получение значений координат конечного пункта.

19. Вычисление приращений и координат разомкнутого теодолитного хода, опирающегося на «твердые» точки и стороны. Контроли вычислений.

Твердыми сторонами принято считать стороны теодолитного хода с известными значениями их дирекционных углов и координат из концов стороны.

Вычисление приращений координат ∆X и ∆Y по дирекционным углам и горизонтальным проложениям сторон теодолитного хода по формулам:

Знаки приращений определить в зависимости от дирекционных углов.

Подсчитывание теоретических сумм приращений координат:

∑∆X_теор =X_кон-X_нач

∑∆Y_теор =Y_кон-Y_нач

Получение невязок приращений координат:

f_∆X=∑∆X_выч -∑∆X_Теор

f_∆Y==∑∆Y_выч -∑∆Y_теор

Вычисление абсолютной и относительной невязки

Вычислить абсолютную невязку ∆Р и относительную невязку /Р.Сравнить ее с допустимой , здесь Р-длина хода

Далее нужно ʄ_∆х и ʄ_∆У распределить на каждое приращение с обратным знаком пропорционально длине линии. Вычислить исправленные значения приращений координат для каждой линии.

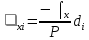
Контроль:=

∆X _iиспр=∆X_вычi+

∆Y _iиспр=∆Y _вычi+

Контроль:

Вычислить координаты Х и У, получая координаты каждой последующей вершины как сумму координат предыдущей вершины с соответствующими исправленными приращениями.

X_i+1 =X_i+∆X_{i испр}

Y_i+1 =Y_i+∆Y_{i испр}

Контроль получение исходных координат: получение значений координат конечного пункта.