Сибирский государственный университет путей сообщения

Кафедра «Инженерная геодезия»

ОБРАБОТКА МАТЕРИАЛОВ ТАХЕОМЕТРИЧЕСКОЙ СЪЕМКИ НА ОСНОВЕ ТЕОДОЛИТНО-ВЫСОТНОГО ХОДА

Руководитель Разработал студент Д-215

___________Жидов В.М ____________Чирков Д.В.

(подпись) (подпись)

____________________ _____________________ (дата проверки) (дата сдачи на проверку)

Краткая рецензия:

______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

(запись о допуске к защите)

________________________ ____________________ (подпись преподавателя) (оценка по результатам защиты)

Новосибирск 2018г.

ОБРАБОТКА МАТЕРИАЛОВ ТЕОДОЛИТНОГО ХОДА

Уравнивание горизонтальных углов.

Контролем измерения и вычисления горизонтальных углов является угловая невязка , которую определяют по формуле:

=

где - сумма измеренных горизонтальных углов; – теоретическая сумма углов.

Теоретическую сумму углов разомкнутого теодолитного хода вычисляют по формуле:

где n – число измеренных углов, не считая примычные (примычными называют углы, образованные одной из сторон хода и «твердым» направлением).

Для оценки качества измерений и вычислений углов определим допустимую невязку, заданную инструкцией:

Так как , то измерения и вычисления углов выполнены правильно. Невязку распределяем поровну во все углы с обратным знаком невязки и округлением до 1'.

Значения поправок записывают в столбец 2 ведомости над значением измеренных углов.

Правильность распределения поправок контролируют по формуле:

Вычисляем исправленные значения горизонтальных углов по формуле:

и записывают в столбец 3 ведомости.

Правильность вычислений исправленных углов контролируют по формуле:

Вычисление дирекционных углов.

Дирекционный угол T – это горизонтальный угол, отсчитываемый от северного направления меридиана или параллельной ему линии по ходу часовой стрелки до заданного направления.

По дирекционному углу начальной стороны и исправленным горизонтальным углам вычисляют дирекционные углы последующих сторон по правилу: дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180 и минус исправленный правый по ходу горизонтальный угол, заключенный между этими сторонами.

Если при вычислении уменьшаемое меньше вычитаемого, то к уменьшаемому прибавляют период 360°. В случае применения другой вычислительной техники порядок действий может быть несколько иным.

Вычисление приращений координат.

Приращения координат X и Y определяются из решения прямой геодезической задачи на координаты. Так как приращение – это проекция стороны на соответствующую ось координат, то используют формулы тригонометрии:

где d – горизонтальное положение стороны хода, соответствующее данному направлению; Т – дирекционный угол стороны, переведенный в градусы.

Вычисление линейных невязок хода.

Точность полевых измерений сторон и углов теодолитного хода характеризуется относительной ошибкой вычисления координат, так как она пропорциональна длине хода.

Относительная линейная невязка – это отношение абсолютной невязки периметра хода к периметру теодолитного хода :

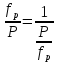
Невязка периметра хода определяется по формуле:

где – невязки в приращениях координат соответственно

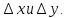
Геометрическая сущность невязок состоит в том, что при измерении горизонтальных углов и длин сторон d допущены ошибки

Для разомкнутого теодолитного хода:

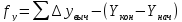
где X_кон и X_нач – абсциссы конечной и начальной точек теодолитного хода; Y_кон, Y_нач – ординаты этих точек.

Относительная ошибка хода 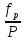должна быть

Если , то невязки распределяют прямо пропорционально длинам сторон с обратным знаком невязки.

Из этого следует, что вычисления выполнены верно.

Поправки приращений координат вычисляются следующим образом:

где d – длина стороны хода, для которой вычисляют поправку в приращениях

При правильном вычислении поправок 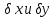их сумма должна равняться невязке с обратным знаком, т.е.

Исправленные приращения координат вычисляют по формулам:

Вычисления контролируются формулами: