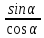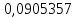Добавил:

qwerty228 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

УПП2КУРС / 1 семестр / ПУТИИИ СООООБЩЕНИЯ / курсовик / файлы / 2_glava_pechat_s_16_stranitsy.docx

Скачиваний:

434

Добавлен:

18.09.2019

Размер:

332.18 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Расчет основных параметров обыкновенного стрелочного перевода, укладываемого в стесненных условиях

2.1 Конструктивная схема обыкновенного стрелочного перевода

Основными элементами современного одиночного обыкновенного стрелочного перевода являются: стрелка, комплект крестовинной части, соединительные пути, подрельсовое основание (рисунок 2.1)

1 – рамные рельсы; 2 – остряки; 3 – переводной механизм; 4 – контррельсы;

5 – усовики; 6 – сердечник крестовины

Рисунок 2.1 – Конструктивная схема обыкновенного стрелочного перевода

Расчетная геометрическая схема обыкновенного стрелочного перевода

Основными характеристиками обыкновенного стрелочного перевода (рисунок 2.2) являются /2/:

α – угол между рабочими гранями крестовины;

tgα = 1/N – марка крестовины;

ЦП – центр стрелочного перевода, т. е. точка пересечения осей прямого и бокового путей;

С – математический центр крестовины, т. е. точка пересечения рабочих граней сердечника;

Рисунок 2.2 – Расчетная геометрическая схема обыкновенного стрелочного перевода

β_н–начальный угол криволинейного остряка;

β – полный стрелочный угол;

L_п – полная длина перевода;

L_т – теоретическая длина перевода;

– большие полуоси перевода;

– малые полуоси перевода;

R₀– радиус криволинейного остряка;

R – радиус переводной кривой;

– длина криволинейного остряка;

– длина прямолинейного остряка;

m₁ – передний вылет рамного рельса;

– длина рамного рельса;

h – передний вылет крестовины;

p – задний вылет крестовины;

y₀ – ордината в корне остряка;

d – прямая вставка;

S₀ – ширина колеи в стрелочном переводе.

2.3 Расчет основных параметров и разбивочных размеров обыкновенного стрелочного перевода, укладываемого в стесненных условиях

2.3.1 Расчет радиуса переводной кривой, длины прямой вставки, малых и больших полуосей стрелочного перевода

Если при укладке стрелочных переводов в стесненных условиях необходимо уменьшить теоретическую длину типового перевода (см. таблицу 2.1) более чем на 250 мм, следует выполнить перерасчет его основных параметров и разбивочных размеров.

Таблица 2.1 – Основные характеристики обыкновенных стрелочных переводов

Тип рельсов стрелочного перевода	Р50
Марка крестовины 1/N	1/11
Длина криволинейного остряка l₀, мм	6 515
Начальный угол остряка β_н, рад	0,0118852
Радиус остряка R₀, мм	297 259
Передний вылет рамного рельса m₁, мм	4323
Длина рамного рельса l_рр, мм	12 500
Передний вылет крестовины h, мм	2 650
Задний вылет крестовины p, мм	2 300
Полная длина стрелочного перевода L_п, мм	33 525

Теоретическая длина стрелочного перевода с учетом уменьшения его длины на Δ (равное 750 мм), определяется по формуле:

(2.1)

При этом практическая длина стрелочного перевода после его укорочения станет равной:

(2.2)

Спроектировав расчетный контур АС (см. рисунок 2.2) на вертикальную и горизонтальную оси, получим систему уравнений:

(2.3)

Решив систему уравнений, определим радиус переводной кривой R и длину прямой вставки d:

, (2.4)

(2.5)

В уравнениях (2.4) – (2.5) еще не определенными являются , и .

Ордината в корне остряка вычисляется по формуле

(2.6)

Проекция криволинейного остряка на рамный рельс – по формуле

(2.7)

Полный стрелочный угол

. (2.8)

Длина заднего вылета рамного рельса определяется по формуле:

(2.9)

Вычисления:

Угол крестовины:

Найдя неизвестные величины, подставляем их в уравнения (2.4) – (2.5):

Малые полуоси стрелочного перевода согласно расчетной схеме (см. рисунок 2.2) определяются по формулам:

(2.10)

. (2.11)

Соответственно большие полуоси:

, (2.12)

, (2.13)

2.3.2 Определение ординат для разбивки переводной кривой стрелочного перевода

При разбивке переводной кривой за начало координат принимается точка А, расположенная на рабочей грани рамного рельса против корня остряка (рисунок 2.3).

Координаты конца переводной кривой определяются по формулам

, (2.14)

. (2.15)

=14484,4 мм,

Рисунок 2.3 – Расчетная схема для определения ординат переводной кривой

Координаты промежуточных точек определяются следующим образом. По оси абсцисс значения x_iназначаются с шагом 2000 мм от x₀=0 до x_k, а ординаты определяются по формуле

, (2.16)

где γ_i определяется из зависимости

. (2.17)

Расчеты удобно проводить в табличной форме (таблица 2.2).

Таблица 2.2 – Расчет ординат переводной кривой


0	0	0,0337957	0,999429	148,8
2000	0,007835	0,0416303	0,999133	224,3
4000	0,015669	0,0494650	0,998776	315,5
6000	0,023504	0,0572996	0,998357	422,4
8000	0,031339	0,0651342	0,997877	545,1
10000	0,039173	0,0729688	0,997334	683,5
12000	0,047008	0,0808035	0,996730	837,7
14000	0,054842	0,0886381	0,996064	1007,8
14484,4	0,05674	0,0905356	0,995893	1051,4

, (2.18)

Составим таблицы тригонометрических функций рассматриваемых углов:

Таблица 2.3 – значение тригонометрических функций угла α

tgα =	α, рад	Sinα	cosα	tgα =	tg
				0,090909	0,045361

Таблица 2.4 – значение тригонометрических функций углов β и β_н

β, рад	cos β	sin β	cos(α- β)	cosβ_н	sinβ_н	tg β
						0,033815

2.3.3 Определение длин рельсовых нитей стрелочного перевода

Исходными данными для определения длин рельсовых нитей укороченного стрелочного перевода являются основные размеры рамных рельсов, остряков, крестовины и всего стрелочного перевода, приведенные в таблице 2.1. и получены расчётом значения L_T, L_ПУ, R с учётом уменьшения его длины на Δ.

Длины рельсов соединительной части определяются из геометрических соображений. При этом положение стыков в конце стрелки определяются длиной рамного рельса и остряка (рисунок 3.2).

Стыки в начале и в хвосте крестовины определяются её длиной; на внешних рельсовых нитях стыки находяься на перпендикуляре к оси каждой из путей.

Соединительные пути между срелкой и крестовиной должны быть разделены на две части так, чтобы рельсы, примыкающие к стрелке l₁,l_3,l_{5 И}l_7,были по возможности кратными длине цельного рельса или частям целых рельсов (25 м, 12,5 м или 6,25 м). Длины других рельсов вычисляются по формулам:

, (2.19)

, (2.20)

, (2.21)

(2.22)

где 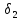= 8 мм – типовой стыковой зазор;

= 8 мм – типовой стыковой зазор в клееболтовом изолирующем стыке;

= 5 мм – стыковой зазор в корне остряка;

= 0 мм – стыковой зазор в стыках крестовины по требованию условий текущего содержания;

– ширина головки рельса, для рельсов Р50 = 72 мм.

Вычисления:

4525,7 мм.

мм.

После этих расчётов может понадобится окончательна корректировка длин рельсов.Прежде всего необходимо иметь в виду, что рельсовые рубки должны быть по возмжности длинными и во всех случаях не короче 4,5 м.

Если вычеслинные по формулам (2.19), (2.20), (2.21), (2.22) какие-то рельсы, например окажутся короче 4,5 м, то все рельсы с чётной нумерацией : ,,, необходимо удлинить на 6,25 м или 12,5 м , а прилегающие к ним рельсы стандартной длины ,,, сделать короче на эти же 6,25 или 12,5 м.

Поскольку короче 4, 5 м, то удлиняем все рельсы с чётной нумерацией на 6,25 м. Прилегающие рельсы с нечётной нумерацией делаем короче на 6, 25 м. Получим:

В соответствии с рисунком 2.2, наружная рельсовая нить прямолинейного соединительного пути состоит из двух рельсов и клееболтового изолирующего стыкового зазора между ними:

(2.23)

20 270,0 мм.

Внутрення рельсовая нить криволинейного соединительного пути также состоит из двух рельсов и и клееболтового изолирующего стыкового зазора между ними: