Билет #3

Дано: q=18 кН/м, M=24 кН*м, F=12 Н.

Вычислить размеры балки прямоугольного сечения: h/b=2, если R_y=160 МПа.

Решение: I. Определение опорных реакций.

1. Рассмотрим равновесие балки.

ΣF_x = 0: H_A = 0

ΣM_A = 0: - q₁*6*(2 + 6/2) + M₁ + R_B*6 + P₁*8 = 0

ΣM_B = 0: - R_A*6 + q₁*6*(4 - 6/2) + M₁ + P₁*2 = 0

2. Вычислим реакции опор

R_B = (q₁*6*(2 + 6/2) - M₁ - P₁*8) / 6 = (18*6*(2 + 6/2) - 24 - 12*8) / 6 = 70 (кН)

R_A = (q₁*6*(4 - 6/2) + M₁ + P₁*2) / 6 = (18*6*(4 - 6/2) + 24 + 12*2) / 6 = 26 (кН)

3. Выполним проверку ΣF_y = 0:

R_A - q₁*6 + R_B + P₁ = 26 - 18*6 + 70 + 12 = 0

II. Построение эпюр.

1-й участок 0 ≤ x₁ < 2

Q(x₁) = + R_A

Q₁(0) = Q₁(2) = 26 (кН)

M(x₁) = + R_A*(x₁)

M₁(0) = 26*0 = 0 (кН*м)

M₁(2) = 26*2 = 52 (кН*м)

2-й участок 2 ≤ x₂ < 4

Q(x₂) = + R_A - q₁*(x₂ - 2)

Q₂(2) = 26 - 18*(2 - 2) = 26 (кН)

Q₂(4) = 26 - 18*(4 - 2) = -10 (кН)

M(x₂) = + R_A*(x₂) - q₁*(x₂ - 2)²/2

M₂(2) = 26*2 - 18*(2 - 2)²/2 = 52 (кН*м)

M₂(4) = 26*4 - 18*(4 - 2)²/2 = 68 (кН*м)

На этом участке эпюра Q пересекает горизонтальную ось. Точка пересечения: x = 3,44. Локальный экстремум в этой точке:

M₂(3,44) = 26*3,44 - 18*(3,44 - 2)²/2 = 70,78 (кН*м)

3-й участок 4 ≤ x₃ < 6

Q(x₃) = + R_A - q₁*(x₃ - 2)

Q₃(4) = 26 - 18*(4 - 2) = -10 (кН)

Q₃(6) = 26 - 18*(6 - 2) = -46 (кН)

M(x₃) = + R_A*(x₃) - q₁*(x₃ - 2)²/2 - M₁

M₃(4) = 26*4 - 18*(4 - 2)²/2 - 24 = 44 (кН*м)

M₃(6) = 26*6 - 18*(6 - 2)²/2 - 24 = -12 (кН*м)

4-й участок 6 ≤ x₄ < 8

Q(x₄) = + R_A - q₁*(x₄ - 2) + R_B

Q₄(6) = 26 - 18*(6 - 2) + 70 = 24 (кН)

Q₄(8) = 26 - 18*(8 - 2) + 70 = -12 (кН)

M(x₄) = + R_A*(x₄) - q₁*(x₄ - 2)²/2 - M₁ + R_B*(x₄ - 6)

M₄(6) = 26*6 - 18*(6 - 2)²/2 - 24 + 70*(6 - 6) = -12 (кН*м)

M₄(8) = 26*8 - 18*(8 - 2)²/2 - 24 + 70*(8 - 6) = 0 (кН*м)

На этом участке эпюра Q пересекает горизонтальную ось. Точка пересечения: x = 7,33. Локальный экстремум в этой точке:

M₄(7,33) = 26*7,33 - 18*(7,33 - 2)²/2 - 24 + 70*(7,33 - 6) = 4 (кН*м)

III. Подбор сечения.

Прямоугольное сечение балки подбираем из условия прочности при допускаемом напряжении: R_y=160 Мпа

Момент сопротивления прямоугольного сечения определим по формуле:

Требуемый момент сопротивления:

Поскольку дано соотношение сторон, то

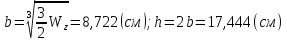
Билет #4

Дано: q=12 кН/м, M=24 кН*м, F=18 Н.

Вычислить размеры балки прямоугольного сечения: h/b=1,5, если R_y=160 МПа.

Решение: I. Определение опорных реакций.

1. Рассмотрим равновесие балки.

ΣF_x = 0: H_A = 0

ΣM_A = 0: - q₁*6*(2 + 6/2) + M₁ + R_B*6 + P₁*4 = 0

ΣM_B = 0: - R_A*6 + q₁*6*(4 - 6/2) + M₁ - P₁*2 = 0

2. Вычислим реакции опор

R_B = (q₁*6*(2 + 6/2) - M₁ - P₁*4) / 6 = (12*6*(2 + 6/2) - 24 - 18*4) / 6 = 44 (кН)

R_A = (q₁*6*(4 - 6/2) + M₁ - P₁*2) / 6 = (12*6*(4 - 6/2) + 24 - 18*2) / 6 = 10 (кН)

3. Выполним проверку ΣF_y = 0:

R_A - q₁*6 + R_B + P₁ = 10 - 12*6 + 44 + 18 = 0

II. Построение эпюр.

1-й участок 0 ≤ x₁ < 2

Q(x₁) = + R_A

Q₁(0) = Q₁(2) = 10 (кН)

M(x₁) = + R_A*(x₁)

M₁(0) = 10*0 = 0 (кН*м)

M₁(2) = 10*2 = 20 (кН*м)

2-й участок 2 ≤ x₂ < 4

Q(x₂) = + R_A - q₁*(x₂ - 2)

Q₂(2) = 10 - 12*(2 - 2) = 10 (кН)

Q₂(4) = 10 - 12*(4 - 2) = -14 (кН)

M(x₂) = + R_A*(x₂) - q₁*(x₂ - 2)²/2

M₂(2) = 10*2 - 12*(2 - 2)²/2 = 20 (кН*м)

M₂(4) = 10*4 - 12*(4 - 2)²/2 = 16 (кН*м)

На этом участке эпюра Q пересекает горизонтальную ось. Точка пересечения: x = 2,83. Локальный экстремум в этой точке:

M₂(2,83) = 10*2,83 - 12*(2,83 - 2)²/2 = 24.17 (кН*м)

3-й участок 4 ≤ x₃ < 6

Q(x₃) = + R_A - q₁*(x₃ - 2) + P₁

Q₃(4) = 10 - 12*(4 - 2) + 18 = 4 (кН)

Q₃(6) = 10 - 12*(6 - 2) + 18 = -20 (кН)

M(x₃) = + R_A*(x₃) - q₁*(x₃ - 2)²/2 + P₁*(x₃ - 4)

M₃(4) = 10*4 - 12*(4 - 2)²/2 + 18*(4 - 4) = 16 (кН*м)

M₃(6) = 10*6 - 12*(6 - 2)²/2 + 18*(6 - 4) = 0 (кН*м)

На этом участке эпюра Q пересекает горизонтальную ось. Точка пересечения: x = 4.33. Локальный экстремум в этой точке:

M₃(4.33) = 10*4,33 - 12*(4,33 - 2)²/2 + 18*(4,33 - 4) = 16.67 (кН*м)

4-й участок 6 ≤ x₄ < 8

Q(x₄) = + R_A - q₁*(x₄ - 2) + P₁ + R_B

Q₄(6) = 10 - 12*(6 - 2) + 18 + 44 = 24 (кН)

Q₄(8) = 10 - 12*(8 - 2) + 18 + 44 = 0 (кН)

M(x₄) = + R_A*(x₄) - q₁*(x₄ - 2)²/2 + P₁*(x₄ - 4) + R_B*(x₄ - 6)

M₄(6) = 10*6 - 12*(6 - 2)²/2 + 18*(6 - 4) + 44*(6 - 6) = 0 (кН*м)

M₄(8) = 10*8 - 12*(8 - 2)²/2 + 18*(8 - 4) + 44*(8 - 6) = 24 (кН*м)