
ФГБОУ ВПО СГУПС
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный уни-
верситет путей сообщения»
А.В. Петухова, И.А. Сергеева
ПРАКТИКУМ ПО ИНЖЕНЕРНОЙ И КОМПЬЮТЕРНОЙ ГРАФИКЕ ДЛЯ СТУДЕНТОВ ФАКУЛЬТЕТА УПП
Часть 1. Проекции геометрических фигур
Новосибирск 2015
1
УДК
Петухова А.В., Сергеева И.А. Практикум по инженерной графике для студентов факультета УПП/ Часть 1. Проекции геометрических образов: Метод. указ. – Новосибирск: Изд-во СГУПСа, 2015. – с.
Практикум содержит цикл задач по темам лекционного курса для аудиторной и самостоятельной работы, вопросы для самоконтроля, варианты контрольных заданий с образцами выполнения.
Предназначены для студентов первого курса факультета УПП специальностей и направлений подготовки: Д, ТБ, ТЛ.
Рассмотрено и рекомендовано к печати на заседании кафедры «Графика».
О т в е т с т в е н н ы й р е д а к т о р:
ст. преп. кафедры «Графика» СГУПС Быкадорова Т.А.
Р е ц е н з е н т ы :
завкафедрой «Инженерная графика и компьютерное моделирование» канд. техн. наук, доцент Лесных А.С.
2
Дисциплина «Инженерная и компьютерная графика» является комплексной и включает в себя разделы начертательной геометрии, технического рисунка и проекционного черчения. Результатом изучения раздела «Проекции геометрических фигур» является умение изображать пространственные объекты на плоскости, а также решать позиционные и метрические задачи. Успешное освоение данного раздела обеспечит качественную работу с проекционными, рабочими и сборочными чертежами.
В практикуме приведены условия задач, предназначенных для решения на практических занятиях, задания на дом и варианты контрольных заданий (эпюров). Задачи разделены соответственно обобщенным темам лекционного курса и имеют сквозную нумерацию. Задания, номера которых подчеркнуты, предназначены, как правило, для самостоятельного выполнения. Также представлен ряд задач повышенной сложности для подготовки к предметной олимпиаде и экзамену.
Принятые обозначения:
Для краткости записи условий задач и алгоритмов их решения примене-
ны следующие обозначения и символы:
( )0 – начало координат; П1, П2, П3 - плоскости проекций: горизонтальная, фронтальная, про-
фильная;
X, Y, Z – оси проекций;
А, В, С, D … или 1, 2, 3 … - точки пространства;
А1, А2, А3 или 11, 12, 13 - проекции точек: горизонтальная, фронтальная, профильная;
АВ, CD, MN … - отрезок прямой;
a, b, c, m … - линия (прямая или кривая);
3
h, f - линии уровня: горизонтальная (горизонталь), фронтальная (фрон-
таль);
n - линия ската, p – перпендикуляр;
α, β, γ, σ, δ … - плоскости в пространстве; Φ, ∆, Σ, Γ, Λ… - поверхности; |АВ| - расстояние между точками;
АВС, В - угол с вершиной в точке В;
||- параллельность геометрических фигур;
- перпендикулярность геометрических фигур;
∩- пересечение фигур;
, - взаимная принадлежность фигур; ≡ - совпадение двух геометрических фигур; = - равенство, результат действия;- подобие геометрических фигур.
1.Варианты аудиторных и домашних задач
Тема 1. Ортогональные проекции точки, прямой, плоскости
Вопросы для самоподготовки:
1.Что называется ортогональной проекцией точки? Эпюром точки?
2.Какие координаты на чертеже определяют удаление точки от плоскостей проекций?
3.Какие точки называются конкурирующими относительно данной плоскости проекций? Определение видимости конкурирующих точек.
4.Проецирующие прямые: основные свойства. Эпюры проецирующих прямых.
5.Линии уровня: основные свойства. Эпюры линий уровня.
4
6.Прямая общего положения. Правило построения натуральной величины данной прямой.
7.Сформулировать свойства точки и прямой.
8.Изображение на эпюре параллельных, пересекающихся и скрещивающихся прямых.
9.При каком условии прямой угол между двумя пересекающимися или скрещивающимися прямыми проецируется на плоскость проекций без искажения?
1, 2. По данным координатам определить положение точек в пространстве и построить их эпюры в системе П1, П2, П3:
1. А(60,20,60); В(50,0,35); С(30,45,0); D(80,0,0); Е(0,30,30); F(0,15,0); К(15,60,45);
2. А(0,40,30); В(80,50,20); С(10,0,60); D(0,0,45); L(30,30,0); N(60,15,30); M(50,0,0);
3. По данному чертежу определить координаты точек и их положение в пространстве.
4. Построить проекции точки А, которая расположена относительно точки В (55,60,50) выше на 20, правее на 30 и дальше от наблюдателя на 40 мм; а также проекции точек С и D, конкурирующих соответственно с точками А и В при условии, что ZA>ZC ,YB<YD на 15 мм. Определить видимость точек.
5. Построить в системе П1, П2, П3 проекции точки А (50,20,30). Добавить эпюры точек В,С и D, конкурирующих с точкой А на П1, П2, П3 соответственно. Определить видимость точек. Записать координаты.
6. Построить комплексный чертеж следующих точек:
-точки А, равноудаленной от П1 и П3;
-точки В, не имеющей удаления от профильной плоскости проекций;
-точки С, принадлежащей оси 0y;
-точки Е, принадлежащей П2;
5

- точки D, конкурирующей с любой из построенных точек. Записать их координаты.
7. На отрезке АВ найти точку С, удаленную от горизонтальной плоскости проекций на 30 мм. Координаты точек: А (70,60,5), В (70,10, 5).
8. Построить недостающую проекцию отрезка СD, пересекающего отре-
зок АВ. Координаты точек: А(60,70,80), В(60,10,15), С(120,40,75), D(45,15,?).
9. Через точку А провести отрезок АВ=70 мм, пересекающий данный отрезок MN. а) АВ||П1 , б) АВ П1 , в) АВ||П2.
6

10. Построить проекции отрезков НL||П1 и FM||П2, пересекающих данный отрезок АВ в точке: НL под углом 45 , FM под углом 30 . НL=FM=80 мм. А (15,20,10) В(75,60,70) ХD=45 мм.
11, 12. Найти натуральную величину отрезка AB и его углы наклона к П1
и П2.
11. А(100,60,20), В(35,15,80).
12. А(20,60,70), В(80,10,40).
13, 14. Через точку А провести отрезок прямой АВ=65 мм, параллельный прямой t. Определить углы наклона АВ к плоскостям проекций.
15. Определить углы наклона ϕ и ψ прямой t.
16. Построить проекции фронтального отрезка АВ, пересекающего данный отрезок CD под углом 90 . АВ=CD.
17. Найти кратчайшее расстояние от точки А до отрезка CD.
18. Построить проекции равностороннего угла АВС. АВ прямой t,
А=90 .
19. На отрезке АВ найти точку С, отстоящую от точки А на 50 мм.
Тема 2. Прямые и точки плоскости. Главные линии плоскости. Конструирование плоскости
7
Вопросы для самоподготовки:
1.Перечислите все способы задания плоскости на чертеже.
2.Сформулируйте условия принадлежности точки и прямой плоскости.
3.Какие прямые называются горизонталью, фронталью и профильной прямой данной плоскости, а также линиями наибольшего наклона плоскости?
4.Какие плоскости называются плоскостями общего положения, уровня и проецирующими? Как выглядят эпюры вышеперечисленных плоскостей?
20, 21. Построить недостающие проекции геометрических элементов, принадлежащих данной плоскости α (№20 пл.α( l ∩m), №21 пл.α( l ||m)).
22. Построить недостающую проекцию многоугольника FBCDE.
23. Построить недостающую проекцию кривой l, принадлежащей плоскости ∆АВС.
24. Построить проекции квадрата АВСD со стороной АВ, смежная сторона которого совпадает с направлением l (l 1).
25. Построить проекции квадрата АВСD со стороной АВ, смежная сторона которого является горизонтальной прямой.
26. Построить проекции квадрата АВСD по его диагоналям ВD и АС. Диагональ ВD совпадает с направлением l (l 1).
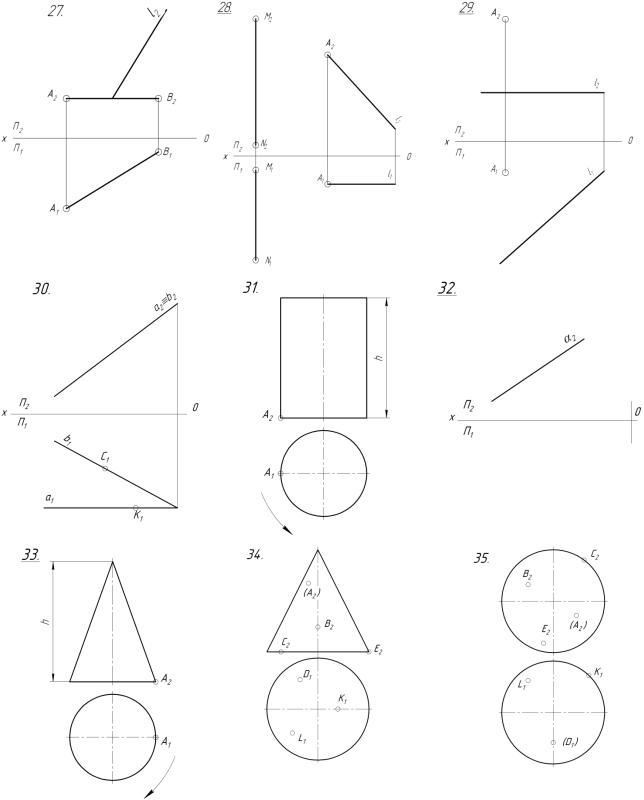
27. Построить проекции равнобедренного треугольника АВС, АВ – основание, СК – высота (совпадает с направлением l (l 2)). АВ=СК.
28. Построить проекции равнобедренного прямоугольного треугольника АВС, в котором А=90 , вершина С MN, сторона АВ - прямой l.
29. Построить проекции равнобедренного треугольника АВС, в котором высота АК равна его основанию ВС. ВС l.
8

9
10
