
- •Дисциплина «Системное программирование» Теоретические вопросы
- •Операционные системы: история
- •Системные вызовы управления терминалом
- •Операционные системы: назначение и основные функции
- •Управление процессами в операционных системах
- •Конкуренция процессов
- •Базовые примитивы доступа к файлам
- •Файлы с несколькими именами
- •Каталоги, файловые системы и специальные файлы
- •Базовые примитивы для работы с процессами.
- •Обработка сигналов в unix Нормальное и аварийное завершение
- •Примитивы межпроцессного взаимодействия: программные каналы.
- •Дополнительные средства межпроцессного взаимодействия в unix.
- •14. Напишите аналог команды ls –l
- •15. Напишите «часы», выдающие текущее время каждые 3 секунды
- •16. Напишите программу, которая ожидает ввода с клавиатуры в течение 10 секунд.Если ничего не введено – печатает «Нет ввода», иначе – «Спасибо».
- •17. Используя файловую систему /proc, получите информацию об открытых всеми процессами файлах
- •18. Напишите функцию mysleep(n), задерживающую выполнение программы на n секунд.
- •19. Составьте программу вывода строк файла в инверсном отображении
- •20. Создайте аналог команды df
- •21. Напишите программу создания и записи образов дискет
- •22. Напишите функции включения и выключения режима эхо-отображения набираемых на клавиатуре символов
- •23. Напишите программу для запуска команды ls в качестве дочернего процесса
- •24. Создайте два процесса, взаимодействующих через программный канал.
- •25.Создайте аналог команды sync
- •Понятие алгоритма. Свойства, способы задания, основные структуры алгоритма. Понятие о структурном подходе к разработке алгоритма.
- •Алгоритмическая структура цикл. Типы циклов. Способы управления циклами. Итерационные циклы. Простые и вложенные циклы.
- •Типы данных в языке Паскаль. Действия над ними. Стандартные типы данных и типы пользователя.
- •Операторы циклов в языке Паскаль. Примеры использования.
- •Цикл с предусловием
- •5.Условный оператор и оператор выбора вариантов в языке Паскаль. Структурная схема. Примеры использования.
- •6 Структурные типы данных. Массивы. Записи, вариантные, вложенные.
- •7.Обработка строковых данных в Паскале. Особенности использования.
- •8.Процедуры и функции в Паскале. Особенности использования.
- •Стандартные файлы и файлы пользователя в Паскале. Типы файлов. Процедуры и функции для работы с файлами.
- •10.Прямая и косвенная рекурсия. Особенности использования.
- •11.Структура языка Паскаль. Структура программ на языке Паскаль.
- •Модульное программирование. Стандартные модули. Назначение и использование.
- •Образцы решений задач
- •1. Написать программу для вычисления функции:
- •2. Сформировать двухмерный массив, состоящий из n X n элементов.
- •5. Задан текст s. Сколько раз в тексте встречается заданное слово (слова разделены пробелами)
- •Дисциплина «Основы баз данных и знаний»
- •1. Архитектура бд. Понятие 3-вой архитектуры бд. Ее преимущества. Внешний уровень. Концептуальный уровень. Внутренний уровень.
- •2. Классификация моделей данных.
- •3. Иерархическая модель. Преимущества и недостатки иерархических структур.
- •4. Сетевая модель данных.
- •5. Реляционная модель данных.
- •6. Нормализация. Пять нормальных форм.
- •7. Физические модели бд.
- •8. Файловые структуры. Файлы прямого доступа. Файлы последовательного доступа.
- •9. Индексные файлы. Индексно-прямые файлы. Индексно-последовательные файлы.
- •10. Распределенные субд. Распределенная обработка данных. Параллельные субд.
- •11. Преимущества и недостатки сурбд.
- •12 Правил Дейта для сурбд.
- •12. Объектно-ориентированные субд. Требования к оосубд.
- •13. Объектно-реляционные субд.
- •14. Структура языка sql.
- •15. Типы данных языка sql.
- •16. Создание схем, бд, таблиц операторами языка sql.
- •17. Индексация в субд. Типы индексов. Создание и удаление индекса операторами языка sql.
- •18. Редактирование данных в таблице бд операторами языка sql.
- •19. Построение запросов операторами языка sql.
- •20. Понятие агрегирующих функций.
- •21. Объединение таблиц. Построение многотабличных запросов операторами языка sql.
- •22. Субд Access. Понятия таблицы, запроса, формы, отчета, макроса.
- •Примеры решений задач
- •Дисциплина «Организация и функционирование эвм»
- •Характеристики жесткого диска.
- •2.Структура дискового сектора. Коды исправления ошибок ecc.
- •3.Назначение коэффициента чередования секторов и коэффициента перекоса головки.
- •4.Сравнительная характеристика интерфейсов жестких дисков.
- •5.Позиционирование магнитной головки. Виды сервосистем.
- •6.Кэширование диска. Виды кэша. (Кэш считывания, кэш со сквозной записью, кэш с отложенной записью и элеваторный кэш).
- •7.Форматирование жесткого диска. Физическое форматирование. Организация разделов на жестком диске.
- •8.Логическое форматирование. Таблица размещения файлов, ее виды.
- •9. Основная оперативная память. Динамическая память, принцип действия запоминающих ячеек. Архитектура динамической памяти, виды сигналов.
- •Типы динамической памяти. Асинхронная, синхронная память.
- •Модули памяти. Организация банков памяти.
- •12.Статическая память, ее разновидности. Кэш-память. Первичный и вторичный кэш.
- •13.Энергонезависимая память, типы памяти. Флэш-память.
- •14.Логическая структура памяти пэвм.
- •15.Сравнительная характеристика видов оптических дисков.
- •16.Сравнительная характеристика видов мониторов.
- •17.Текстовый и графический режим работы монитора. Формирование цвета.
- •18.Сравнительная характеристика видов принтеров.
- •«Теория автоматического управления»
- •Классификация сау
- •Связь входа и выхода. Способы построения моделей. Переходная функция и импульсная характеристика.
- •Типовые звенья линейных систем (усилитель, апериодическое звено, интегрирующее звено, колебательное звено, звено запаздывания).
- •4. Типовые звенья линейных систем (усилитель, апериодическое звено, интегрирующее звено, колебательное звено, звено запаздывания).
- •5. Частотные характеристики. Понятие лачх и лфчх.
- •6. Логарифмические частотные характеристики типовых линейных звеньев.
- •7. Структурные схемы и правила их преобразования.
- •8. Требования к системам автоматического управления (перечислить). Понятие точности управления.
- •9. Частотные критерии устойчивости. Критерий Найквиста.
- •10. Алгебраические критерии устойчивости. Критерий Гурвица. Критерий Вишнеградского.
- •11. Оценка качества системы. Запасы устойчивости.
- •12. Синтез регуляторов. Задачи синтеза
- •13. Синтез линейны непрерывных сау. Коррекция сау
- •14. Разновидности и свойства сау в зависимости от параметров синтеза.
- •15. Приведение задач тау к нулевым начальным условиям. Линеаризация математического описания системы.
- •16. Математические модели. Способы их построения. Линейность и нелиней-ность систем и моделей.
- •17. Преобразование произвольного сигнала линейным звеном
- •18. Интегральные оценки качества переходных процессов: линейные, квадра-тичные.
- •19. Типовые линейные законы регулирования. Виды регуляторов.
- •20. Расчет оптимальных параметров настройки регуляторов.
- •8.Характеристическое уравнение замкнутой системы
5. Частотные характеристики. Понятие лачх и лфчх.
ЛАЧХ
На графике ЛАЧХ абсциссой является частота в логарифмическом масштабе, по оси ординат отложена амплитуда передаточной функции в децибелах.
Представление
АЧХ в логарифмическом масштабе упрощает
построение характеристик сложных
систем, так как позволяет заменить
операцию перемножения АЧХ звеньев
сложением, что вытекает из свойства
логарифма:
![]()
ЛФЧХ
На графике фазо-частотной характеристики абсциссой является частота в логарифмическом масштабе, по оси ординат отложен фазовый сдвиг выходного сигнала системы относительно входного (обычно в градусах).
Также возможен вариант, когда по оси ординат откладывается фазовый сдвиг в логарифмическом масштабе, в этом случае характеристика будет называться ЛФЧХ.
6. Логарифмические частотные характеристики типовых линейных звеньев.
Частотные характеристики достаточно сложно строить вручную. В 60-е годы, когда развивалась классическая теория управления, не было мощных компьютеров, поэтому наибольшую популярность приобрели приближенные методы, с помощью которых можно было проектировать регуляторы с помощью ручных вычислений и построений. Один из таких подходов основа на использовании логарифмических частотных характеристик.
Вместо A(ω) было предложено использовать логарифмическую амплитудную частотных
характеристику (ЛАЧХ): график, на котором по оси абсцисс откладывается десятичный логарифм частоты ( lgω ), а по оси ординат – величина L (ω) 20lg A(ω) m = , измеряемая в децибелах (дБ). При построении логарифмической фазовой частотной характеристики (ЛФЧХ) по оси абсцисс также откладывается логарифм частоты lgω .
Единицей отсчета на логарифмической оси частот является декада – диапазон, на котором
частота увеличивается в 10 раз (а значение ее логарифма увеличивается на единицу). Вместе ЛАЧХ и ЛФЧХ называются логарифмической амплитудно-фазовой частотной характеристикой (ЛАФЧХ) или диаграммой Боде.
Логарифмические характеристики обладают двумя ценными свойствами:
1)
ЛАЧХ и ЛФЧХ для произведения
![]() вычисляются как суммы ЛАЧХ и ЛФЧХ
отдельных звеньев:
вычисляются как суммы ЛАЧХ и ЛФЧХ
отдельных звеньев:
![]()
2) в области высоких и низких частот ЛАЧХ асимптотически приближаются к прямым,
наклон которых составляет ± 20 дБ/дек (децибел на декаду), ± 40 дБ/дек и т.д.
В классической теории управления хорошо разработаны методы анализа и синтеза систем
на основе асимптотических ЛАЧХ, которые представляют собой ломаные линии и легко строятся вручную. C появлением компьютерных средств расчета практическая ценность ЛАФЧХ несколько снизилась, однако они по сей день остаются простейшим инструментом прикидочных расчетов для инженера.
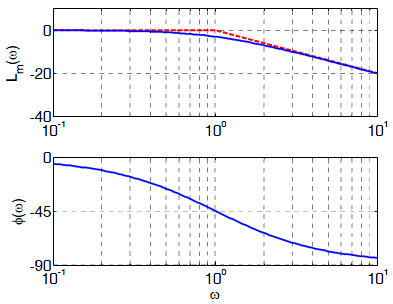
На
рисунке показаны точная (сплошная синяя
линия) и асимптотическая (штриховая
красная линия) ЛАФЧХ для звена первого
порядка с передаточной функцией
![]()
Первая
асимптота, определяющая поведение ЛАЧХ
на
низких частотах,
имеет нулевой наклон, потому что звено
относится к классу позиционных
звеньев,
имеющих постоянный ненулевой статический
коэффициент усиления, то есть![]()
Если W(0) = 0 , передаточная функция содержит множитель sk ( k > 0 ), который соответ-
ствует производной порядка k . В этом случае наклон ЛАЧХ на низких частотах равен
k ⋅ 20 дБ/дек.
Если W(0) = ∞ , звено содержит один или несколько интеграторов, то есть в знаменателе есть сомножитель sk . Тогда наклон ЛАЧХ на низких частотах равен − k ⋅ 20 дБ/дек.
Наклон ЛАЧХ на высоких частотах определяется разностью степеней числителя и знаменателя передаточной функции. Если числитель имеет степень m , а знаменатель – степень n , то наклон последней асимптоты равен 20⋅ (m− n) дБ/дек. В нашем примере m− n = 0 −1 = −1. Поэтому вторая асимптота, определяющая свойства звена на высоких частотах, имеет наклон− 20 дБ/дек, то есть, за одну декаду значение уменьшается на 20 дБ (проверьте по графику!).
