
- •Операції над лінійними операторами
- •Область значень і ядро лінійного оператора
- •Вироджені і невироджені оператори
- •Обернений оператор
- •Інваріантні підпростори. Власні вектори і власні значення лінійного оператора
- •Характеристичне рівняння лінійного оператора
- •Властивості власних векторів та власних чисел.
- •Лінійні оператори з простим спектром.
- •Зведення матриці до діагонального вигляду.
- •Задачі рекомендовані для розв‘язування в аудиторії
- •Задачі рекомендовані для розв‘язування дома
- •Задачі підвищеної складності
Властивості власних векторів та власних чисел.
1. У
дійсному просторі власними числами
будуть лише дійсні корені характеристичного
рівняння
![]() а
в комплексному просторі – усі корені
рівняння
а
в комплексному просторі – усі корені
рівняння
![]() .
.
2. Якщо всі власні числа матриці різні, то всі її власні вектори лінійно незалежні.
3. Кожному власному вектору відповідає одне власне число.
4. Якщо
-
власний вектор матриці
з власним числом
,
то будь-який вектор
![]() ,
колінеарний вектору
,
також є власним вектором матриці
з тим самим власним числом.
,
колінеарний вектору
,
також є власним вектором матриці
з тим самим власним числом.
5. Якщо
![]() і
і
![]() - власні вектори матриці
з одним і тим самим власним числом
,
то їх сума
- власні вектори матриці
з одним і тим самим власним числом
,
то їх сума
![]() також є власним вектором матриці
з тим самим власним числом.
також є власним вектором матриці
з тим самим власним числом.
6. Якщо
квадратна матриця
порядку
має різні власні числа, то матриця
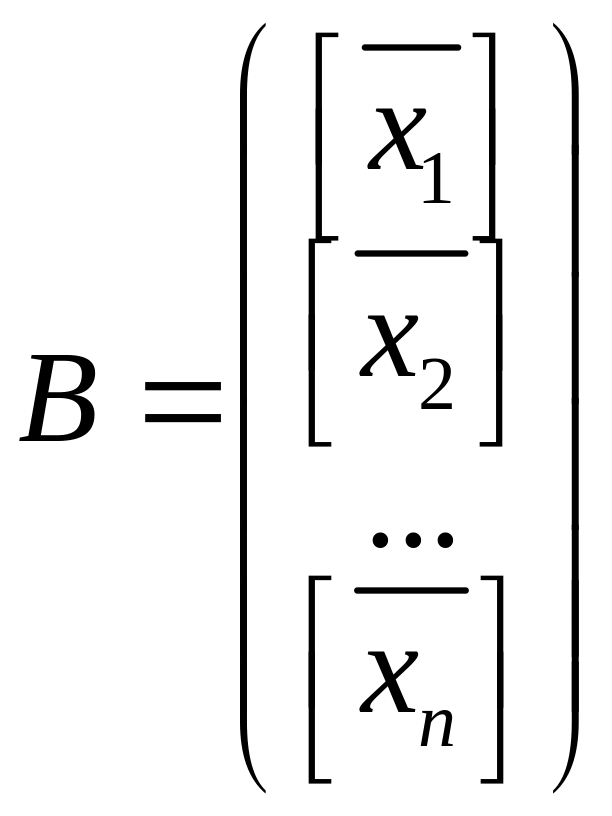 ,
рядками якої є власні вектори
,
рядками якої є власні вектори
![]() має обернену матрицю
має обернену матрицю
![]()
7. Якщо
квадратна матриця
порядку
має різні власні числа
![]() ,
то матрицю
можна звести до діагонального вигляду:
,
то матрицю
можна звести до діагонального вигляду:
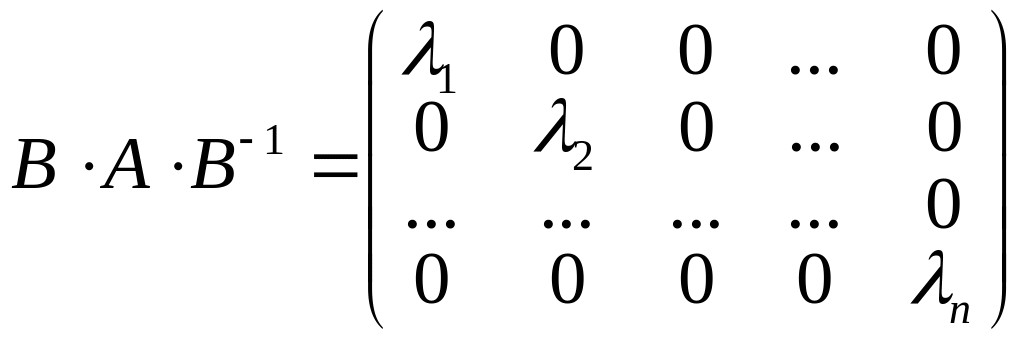 ,
,
який називають канонічною формою Жордана матриці .
Лінійні оператори з простим спектром.
Серед лінійних операторів найпростіші є ті, які мають простий спектр.
Теорема
18. Якщо
вектори базису
![]() є
власними векторами лінійного оператора
,
то в базисі
оператор
задається діагональною матрицею.
Навпаки, якщо в деякому базисі матриця
оператора
є діагональною, то всі вектори цього
базису є власними векторами оператора
.
є
власними векторами лінійного оператора
,
то в базисі
оператор
задається діагональною матрицею.
Навпаки, якщо в деякому базисі матриця
оператора
є діагональною, то всі вектори цього
базису є власними векторами оператора
.
Теорема
19. Для
того, щоб в лінійному просторі
лінійний оператор
мав базис із власних векторів, необхідно
і достатньо, щоб всі характеристичні
числа
![]() оператора
належали основному полю, і щоб кожному
числу
відповідало стільки лінійно незалежних
власних векторів оператора
,
яка алгебраїчна кратність кореня
характеристичного многочленна оператора
.
оператора
належали основному полю, і щоб кожному
числу
відповідало стільки лінійно незалежних
власних векторів оператора
,
яка алгебраїчна кратність кореня
характеристичного многочленна оператора
.
Для
того, щоб матриця
була матрицею простої структури, тобто,
щоб вона зводилась до діагонального
вигляду, необхідно і достатньо, щоб всі
характеристичні корені
матриці
належали основному полю і щоб для кожного
кореня
його геометрична кратність
![]() (
(![]() -
ранг матриці
-
ранг матриці
![]() )
співпадала з алгебраїчною кратністю
)
співпадала з алгебраїчною кратністю
![]() ,
тобто з кратністю кореня
характеристичного многочлена
матриці
.
,
тобто з кратністю кореня
характеристичного многочлена
матриці
.
Теорема 20. Якщо лінійний оператор має простий спектр, то існує базис простору , в якому цей оператор задається діагональною матрицею.
Геометричне тлумачення оператора з простим спектром.
Кожний
вектор
![]()
![]() вибраного базису
визначає одновимірний інваріантний
підпростір
вибраного базису
визначає одновимірний інваріантний
підпростір
![]() ,
який природно розглядати як координатну
вісь простору
.
Дію оператора
на вектори осі
можна характеризувати як «розтяг у
,
який природно розглядати як координатну
вісь простору
.
Дію оператора
на вектори осі
можна характеризувати як «розтяг у
![]() разів» (
-
власне значення, яке відповідає вектору
).
разів» (
-
власне значення, яке відповідає вектору
).
Довільний
елемент
є сума векторів
![]() ,
тобто розкладається по згаданих осях.
Тому, для того, щоб дістати образ
цього елемента, досить кожний складовий
вектор
,
тобто розкладається по згаданих осях.
Тому, для того, щоб дістати образ
цього елемента, досить кожний складовий
вектор
![]() розтягнути у
разів:
розтягнути у
разів:
 .
.
Зведення матриці до діагонального вигляду.
Теорема 21. Кожна квадратна матриця го порядку над полем , яка має у полі різних характеристичних коренів, подібна до деякої діагональної матриці, тобто зводиться до діагонального вигляду.
Методичні рекомендації до розв‘язування задач
Приклад
1.
 матриця
оператора
в базисі
матриця
оператора
в базисі
![]()
![]() ;
;
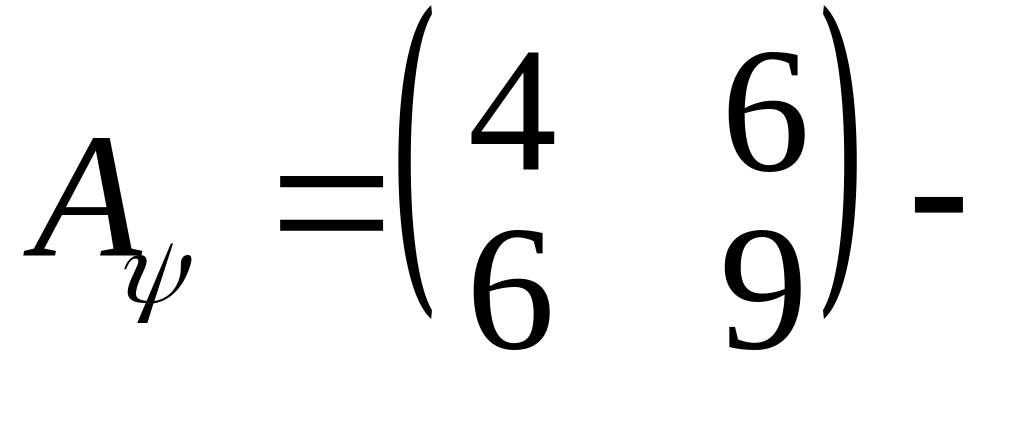 матриця
оператора
в базисі
матриця
оператора
в базисі
![]()
![]() .
Знайти матрицю оператора
.
Знайти матрицю оператора
![]() в базисі
в базисі
![]() .
.
Розв’язання.
Позначимо матрицю оператора
![]() :
:
![]() ,
тоді в базисі
:
,
тоді в базисі
:
![]() ,
де
,
де
![]() -
матриця оператора
в базисі
.
За формулою
-
матриця оператора
в базисі
.
За формулою
![]() ,
де
,
де
![]() -
матриця переходу від базису
до базису
.
Обчислимо
.
-
матриця переходу від базису
до базису
.
Обчислимо
.
![]() ,
,
![]()
 ,
,
![]() ,
,
 .
.
 ,
,
![]() ,
,
 .
.
Тоді
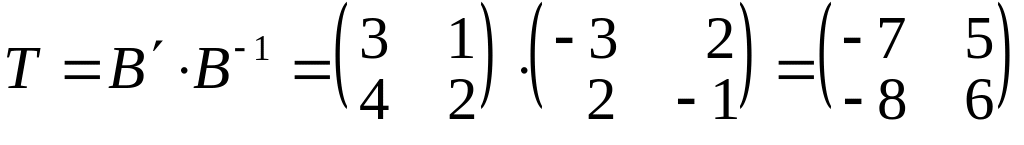 .
.
 .
.
Обчислимо

 .
.
Отже,
 .
.
Відповідь:
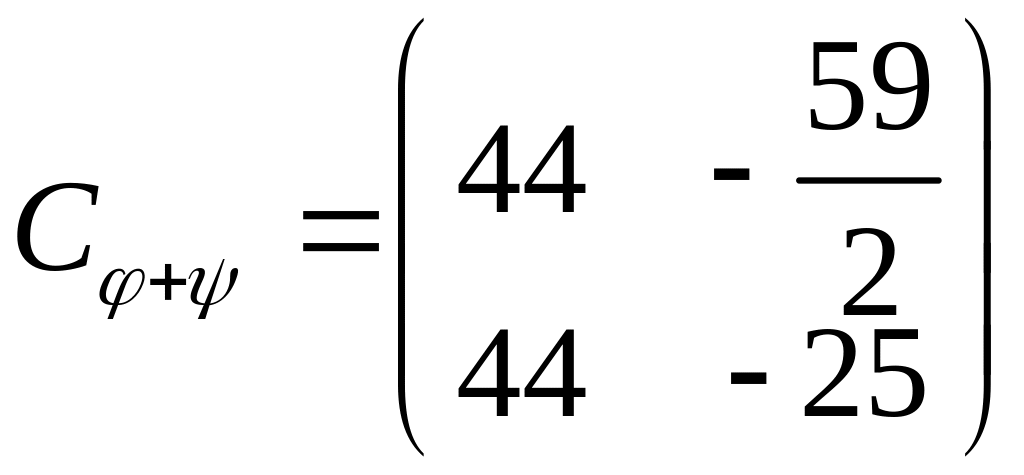 .
.
Приклад
2.
Лінійний
оператор
в базисі
![]() ,
де
,
де
![]() ,
,
![]() має матрицю
має матрицю
 .
Лінійний оператор
в базисі
.
Лінійний оператор
в базисі
![]() ,
де
,
де
![]() ,
,
![]() має матрицю
має матрицю
 .
Знайти
.
Знайти
![]() в базисі
в базисі
![]() ,
де
,
де
![]() ,
,
![]() .
.
Розв’язання. Для того, щоб знайти матрицю в базисі , необхідно обчислити матриці лінійних операторів і в базисі .
Обчислимо
матриці цих операторів в базисі
за формулами
![]() ,
,
![]() ,
де
,
де
![]() -
матриця переходу від базису
-
матриця переходу від базису
![]() до
.
до
.
![]() -
матриця переходу від базису
-
матриця переходу від базису
![]() до
.
до
.
![]()
![]()
 ,
,
![]() ,
,
 .
.
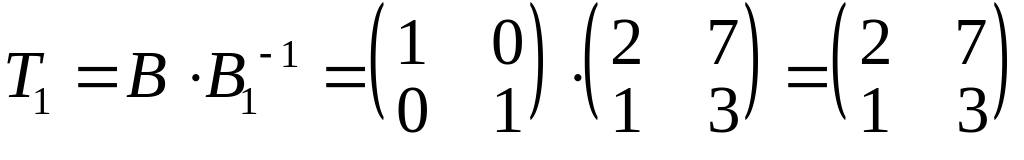 .
.
![]() .
.
 ,
,
![]() ,
,
 .
.
 .
.
Обчислимо
![]() і
і
![]() .
.
 ,
,
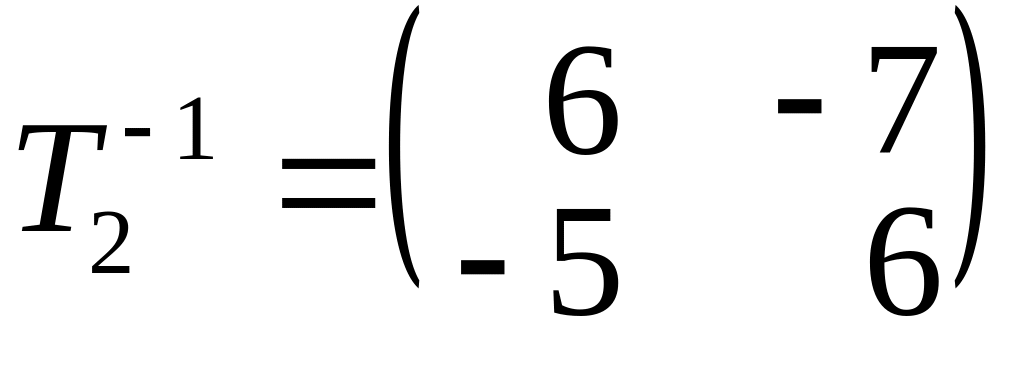 .
.
Отже,

 .
.
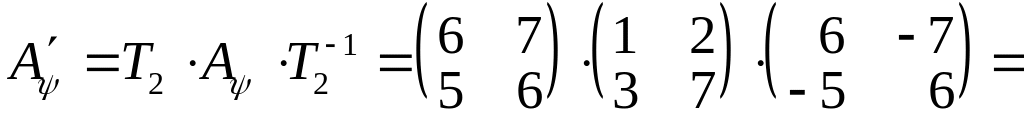
![]() .
.
 .
.
Відповідь:
 .
.
Приклад
3.
Нехай
![]() і
та
– лінійні оператори простору
і
та
– лінійні оператори простору
![]() .
.
![]() ,
,
![]()
![]() .
Знайти: а)
.
Знайти: а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
Розв’язання. При розв’язуванні задачі скористаємося означенням суми та добутку лінійних операторів:
![]() ;
;
![]() .
.
а)
![]() ,
,
![]() ,
,
![]() Матриця
цього перетворення має вигляд:
Матриця
цього перетворення має вигляд:
 .
.
Другий спосіб. Знайдемо матриці перетворення лінійних операторів і .
 ,
,
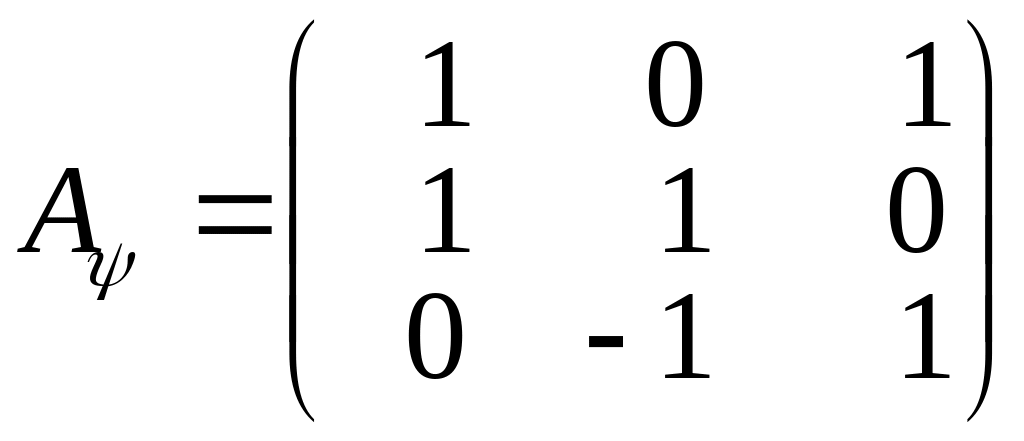 .
.
Виконаємо перетворення:


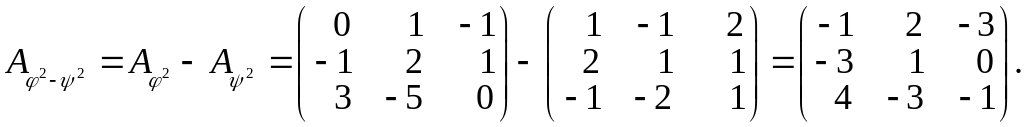 Відповідь:
Відповідь:
![]() .
.
.
б)
![]()
![]()
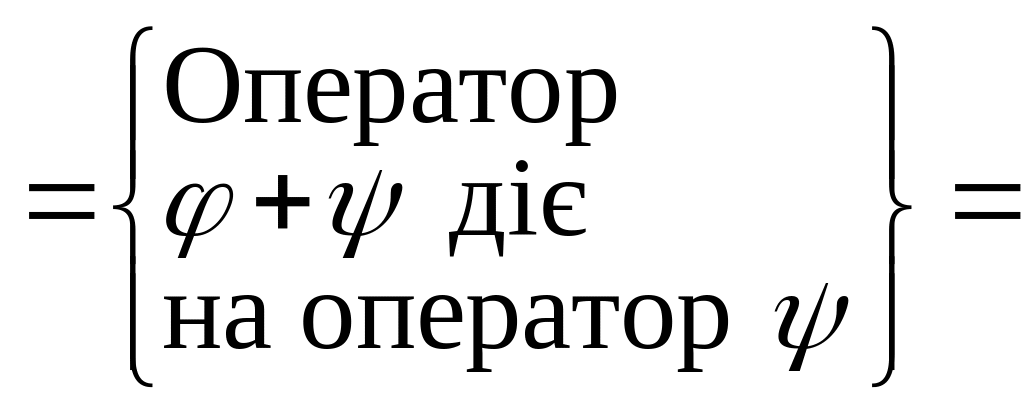
![]()
![]()
![]() .
.
![]() ;
;
![]()
![]()
![]()
 .
.
Другий спосіб.
Розглянемо
![]() ,
де
,
де
![]() .
Подіємо лінійними операторами
та
на вектори базису
.
Подіємо лінійними операторами
та
на вектори базису
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ;
; ![]() .
.
і .
Тоді
 .
.
За означенням, матриця добутку лінійних операторів дорівнює добутку матриць лінійних операторів.
.

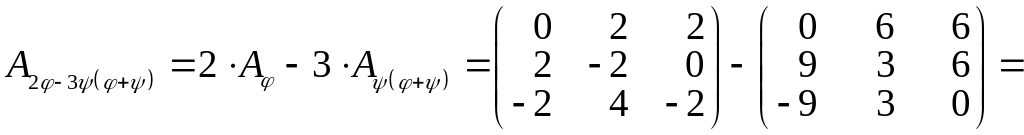
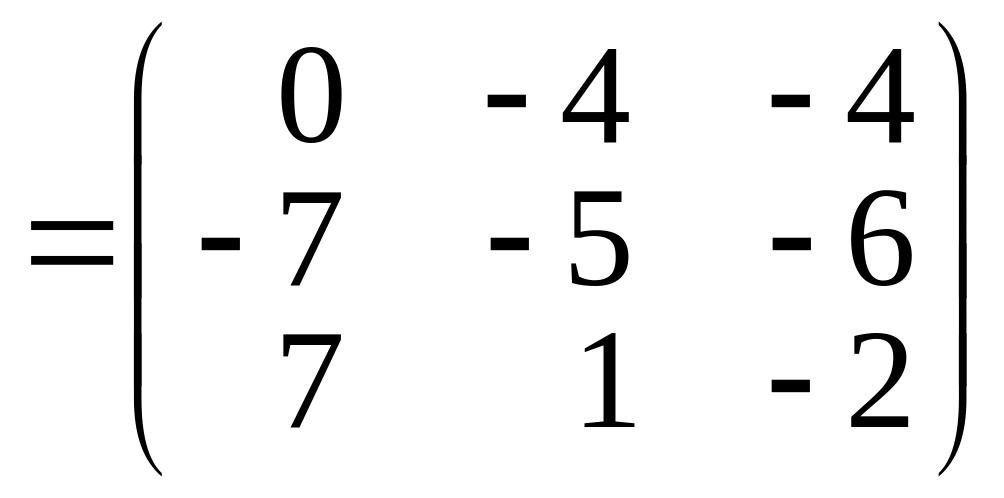 .
.
Відповідь:
![]() ;
;
![]()
 .
.
в)![]()

![]()
![]()
![]()
![]() .
.
Матриця цього перетворення має вигляд:
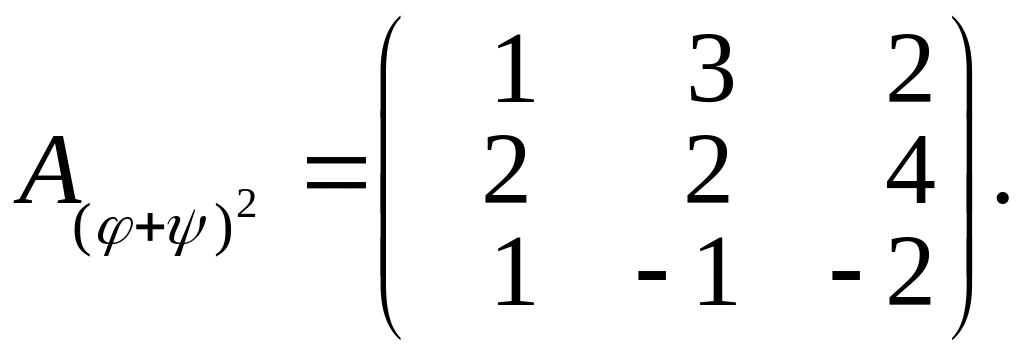
Другий спосіб.
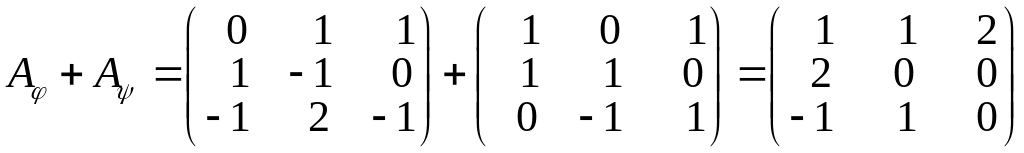 .
.
 .
.
Відповідь:![]() ,
,
 .
.
Приклад
4.
Нехай
і
та
– лінійні оператори простору
.
![]() ,
,
![]() ..
Знайти
..
Знайти
![]() в тому ж базисі.
в тому ж базисі.
Розв’язання. I. За означеннями дій над лінійними операторами, знаходимо:
![]() ,
,
![]() .{оператор
діє
на вектор
}.
.{оператор
діє
на вектор
}.
![]() .
.
Знайдемо матрицю, яка відповідає результату дій над даними лінійними операторами:
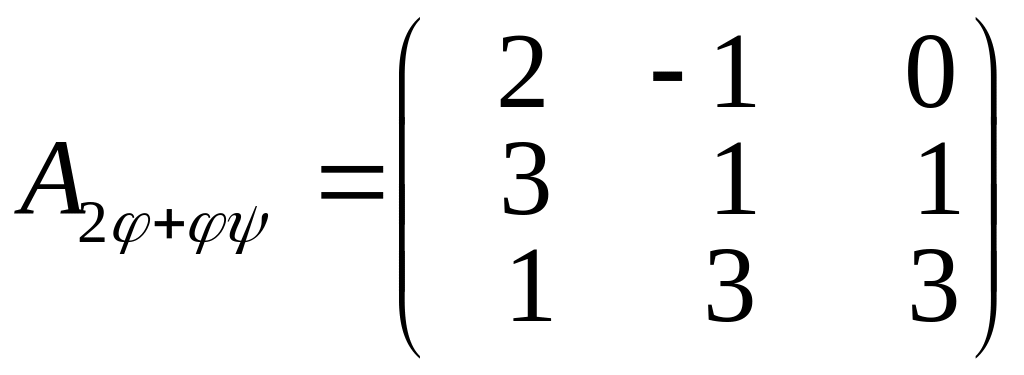 .
.
II. Знайдемо матриці операторів і :
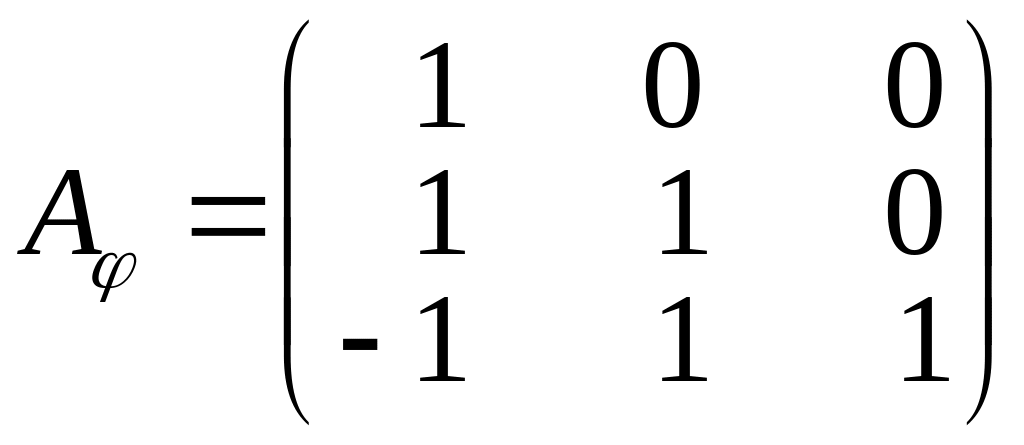 ,
,  .
.
За правилами множення матриць, додавання матриць і множення матриці на число, обчислюємо:

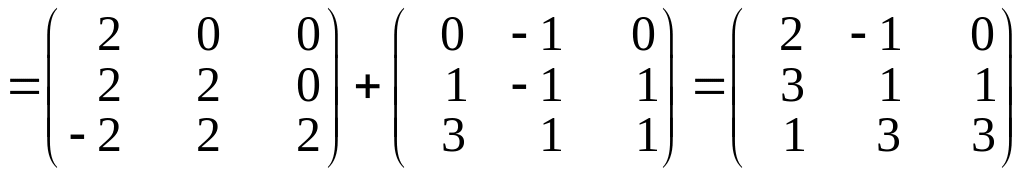 .
.
Знайдемо
координатний рядок образа вектора
,
якщо діє оператор
![]() .
.
 .
.
![]() .
.
Відповідь:
![]() ,
.
,
.
Приклад
5.
Нехай
лінійний оператор
векторного простору
над полем дійсних чисел
![]() у деякому базисі
цього простору задано матрицею: а)
у деякому базисі
цього простору задано матрицею: а) ,
б)
,
б)
 ,
,
в)
 .
Знайти ранг
і дефект
.
Знайти ранг
і дефект
![]() лінійного оператора
.
Побудувати ядро
і область значень
оператора
.
лінійного оператора
.
Побудувати ядро
і область значень
оператора
.
Розв’язання.
а)
Оскільки ранг
![]() лінійного оператора
простору
дорівнює
рангу
лінійного оператора
простору
дорівнює
рангу
![]() матриці
цього
оператора в базисі
,
то знаходимо спочатку
:
матриці
цього
оператора в базисі
,
то знаходимо спочатку
:
![]() ~
~ IIp+5·IIIp ~
IIp+5·IIIp ~
 .
.
Звідси
![]() і тому
і тому
![]() .
.
Внаслідок
того, що сума рангу і дефекту довільного
лінійного оператора векторного простору
дорівнює розмірності цього простору,
то
![]() ,
,
![]() .
.
Для побудови ядра і області значень оператора досить визначити їх базиси.
Оскільки
область значень
оператора
складається з образів усіх векторів
простору
,
тобто з усіх векторів виду
![]() ,
де
,
де
![]() ,
то
підпростір
породжується системою векторів
,
то
підпростір
породжується системою векторів
![]() ,
,
![]() ,
,
![]() .
(а)
.
(а)
Отже, за базис підпростору можна взяти довільну максимальну лінійно незалежну підсистему векторів системи (а).
Оскільки
![]()
![]()
![]()
то такі підсистеми визначаються максимальними лінійно незалежними підсистемами рядків матриці . Із знаходження рангу матриці видно, що однією з максимальних лінійно незалежних підсистем рядків цієї матриці є підсистема, яка складається з першого та третього рядків матриці. Тоді за базис підпростору можна взяти вектори , .
Побудуємо
ядро
лінійного оператора
.
Оскільки вектор
![]() належить до ядра
оператора
тоді і тільки тоді, коли
належить до ядра
оператора
тоді і тільки тоді, коли
![]() ,
тобто коли
,
тобто коли
![]() ,
де
,
де
![]() і
і
![]() - координатні рядки векторів
і
в базисі
,
то
є множина всіх тих векторів простору
,
координатні рядки яких у базисі
,
розглядувані як числові вектори,
утворюють простір розв’язків такої
системи лінійних однорідних рівнянь
- координатні рядки векторів
і
в базисі
,
то
є множина всіх тих векторів простору
,
координатні рядки яких у базисі
,
розглядувані як числові вектори,
утворюють простір розв’язків такої
системи лінійних однорідних рівнянь
![]() ,
або в розгорнутому вигляді
,
або в розгорнутому вигляді
 (б)
(б)
Оскільки
матриця останньої системи є матрицею,
транспонованою до матриці
,
то, використовуючи процес знаходження
рангу матриці
,
можна стверджувати, що ранг цієї системи
дорівнює числу 2 і що за вільне невідоме
можна взяти
![]() .
Тоді
.
Тоді
 ,
,
 -
загальний розв’язок системи (б),
а
-
загальний розв’язок системи (б),
а
![]() =
=
![]() – фундаментальна система розв’язків
системи (б),
яка є базисом простору
.
– фундаментальна система розв’язків
системи (б),
яка є базисом простору
.
Зауваження. Надалі, розв’язуючи такі задачі, ми спрощуватимемо процес розв’язання, а саме:
1.
Знайдемо
ранг
![]() матриці
.
Це буде розмірність
області значень
заданого оператора
.
Тоді розмірність
матриці
.
Це буде розмірність
області значень
заданого оператора
.
Тоді розмірність
![]() ядра
оператора
знайдемо з рівності
ядра
оператора
знайдемо з рівності
![]() ,
де
розмірність усього простору.
,
де
розмірність усього простору.
2.
Визначимо
базис
![]() простору
.
Тут
простору
.
Тут
![]() – номери тих рядків матриці
,
які складають максимальну лінійно
незалежну систему рядків цієї матриці
(зрозуміло, що числа
визначаються
неоднозначно).
– номери тих рядків матриці
,
які складають максимальну лінійно
незалежну систему рядків цієї матриці
(зрозуміло, що числа
визначаються
неоднозначно).
3. Знайдемо фундаментальну систему розв’язків системи лінійних однорідних рівнянь, матрицею якої є матриця, транспонована до матриці . Базис простору і буде ( також, очевидно, визначається однозначно).
б)
![]() =?
=?
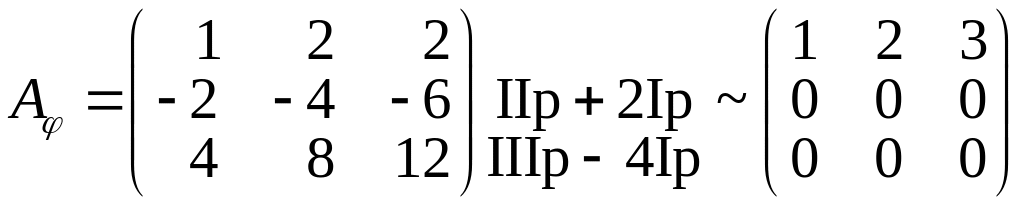 ,
,
![]() .
.
Отже,
![]() ,
де
,
де
![]() .
.
![]()
![]() базис
складається із двох векторів.
базис
складається із двох векторів.
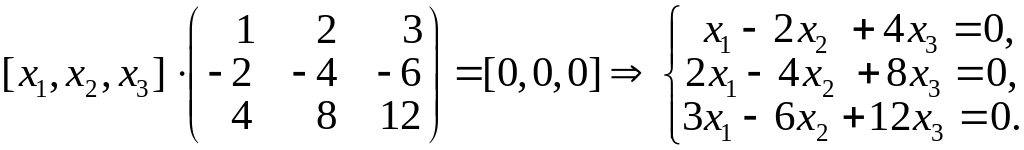
Загальний
розв’язок останньої системи:
![]() .
Фундаментальна система розв’язків
останньої системи складається із
векторів
.
Фундаментальна система розв’язків
останньої системи складається із
векторів
![]() .
.
Отже,
базис
складається із векторів
![]() і
і
![]() .
.
![]() .
.
в)
 ,
,
![]() .
.
Отже,
![]() ,
де
,
де
![]() ,
,
![]() ,
,
![]() .
.
![]() базис
складається
з
базис
складається
з
![]() .
.
Приклад
6.
Лінійний
оператор
в базисі
![]() має матрицю
має матрицю
 ,
а лінійний оператор
в базисі
,
а лінійний оператор
в базисі
![]() має матрицю
має матрицю
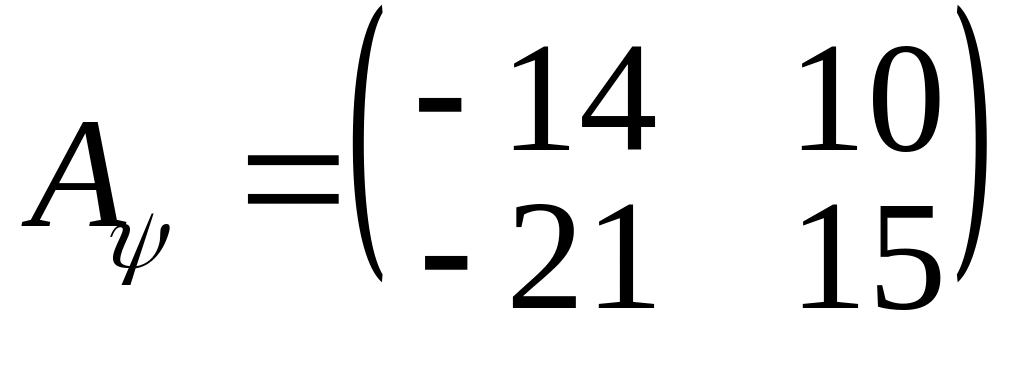 .
Знайти матриці лінійних операторів
.
Знайти матриці лінійних операторів
![]() та
та
![]() в базисі, в якому задано координати всіх
векторів.
в базисі, в якому задано координати всіх
векторів.
Розв’язання.
Введемо позначення
 ,
,
 для заданих базисів і
для заданих базисів і
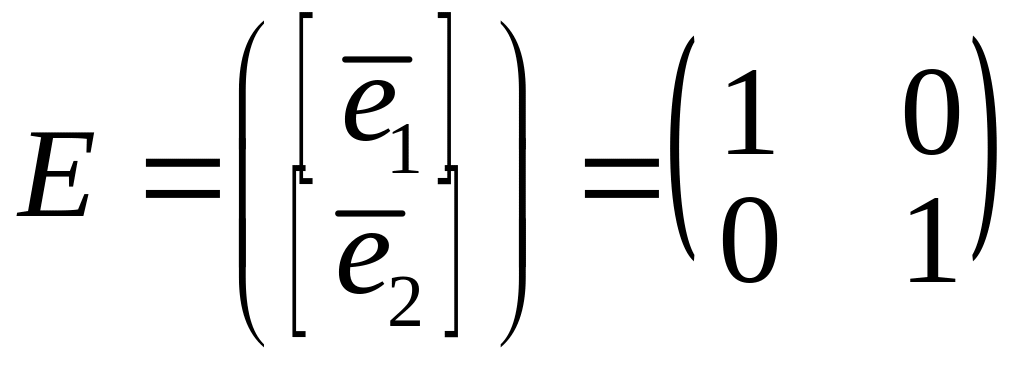 для базису, в якому задано координати
векторів. Завдання полягає в тому, щоб
знайти матриці, що відповідають добуткам
лінійних операторів
та
.
для базису, в якому задано координати
векторів. Завдання полягає в тому, щоб
знайти матриці, що відповідають добуткам
лінійних операторів
та
.
Матрицю
лінійного оператора
в базисі
позначимо
,
а оператора
-
![]() .
.
Тоді
![]() і
і
![]() .
.
За формулою обчислення матриці лінійного оператора в іншому базисі:
і
, де
![]() і
і
![]() -
матриці переходу від базисів
і
до базису
відповідно.
-
матриці переходу від базисів
і
до базису
відповідно.
Оскільки
матриці
і
,
рядки яких складено відповідно з
координатних рядків векторів
![]() і
і
![]() ,
є матрицями переходу від базису
до базисів
і
відповідно, то, враховуючи зв'язок між
матрицями переходу від одного базису
до іншого, дістанемо рівності
,
є матрицями переходу від базису
до базисів
і
відповідно, то, враховуючи зв'язок між
матрицями переходу від одного базису
до іншого, дістанемо рівності
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Тоді
![]() і
і
![]() .
.
Обчислимо послідовно:
 ,
,
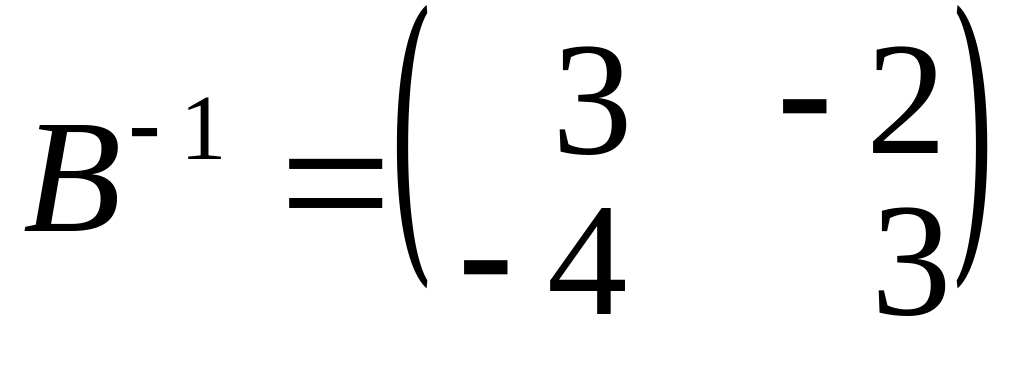 .
.
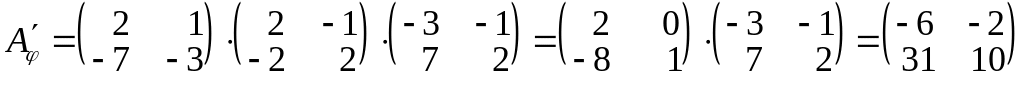 .
.
 .
.
Обчислюємо шукані матриці:
 .
.
 .
.
Відповідь:
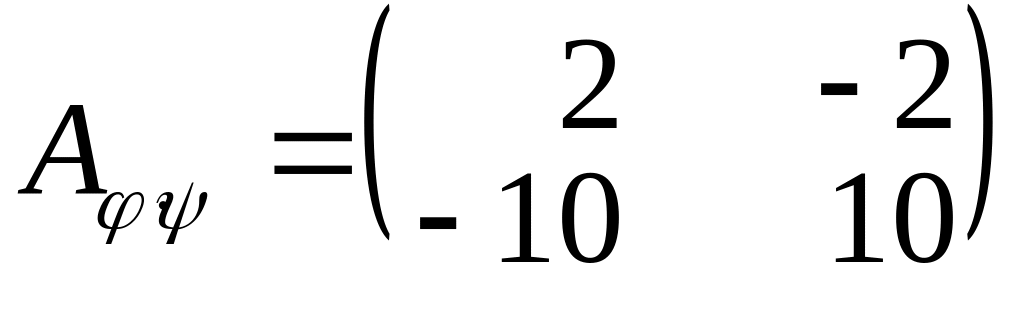 ,
,
 .
.
Приклад
7.
В
лінійному просторі
![]() заданий базис
заданий базис
![]() .
Лінійний оператор
переводить вектори
з координатами
.
Лінійний оператор
переводить вектори
з координатами
![]() ,
,
![]() відповідно у вектори
з координатами
відповідно у вектори
з координатами
![]() ,
,
![]() .
Знайти матрицю оператора
в базисі
.
.
Знайти матрицю оператора
в базисі
.
Розв’язання.
Через
позначимо оператор, який переводить
вектори
![]() у
вектори
.
Його матрицею у базисі
буде
у
вектори
.
Його матрицею у базисі
буде
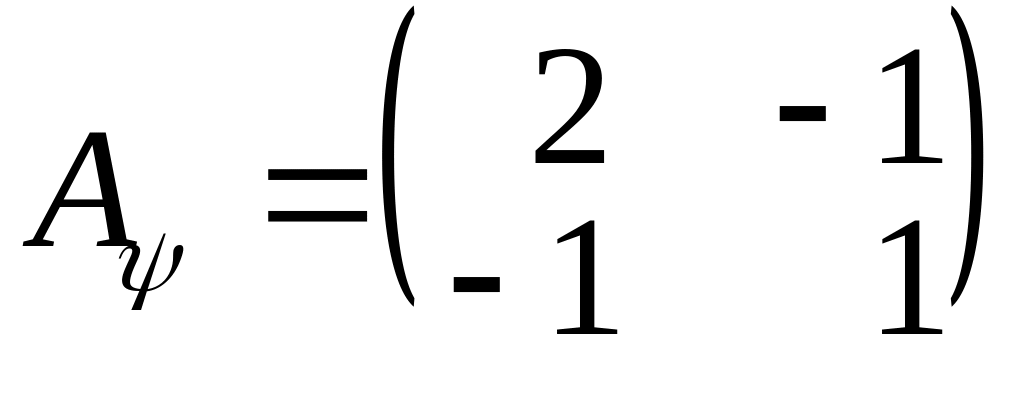 .
.
Оператор переводить вектори у вектори . Отже, добуток операторів і переводить вектори у вектори . Тому в базисі оператор має матрицю
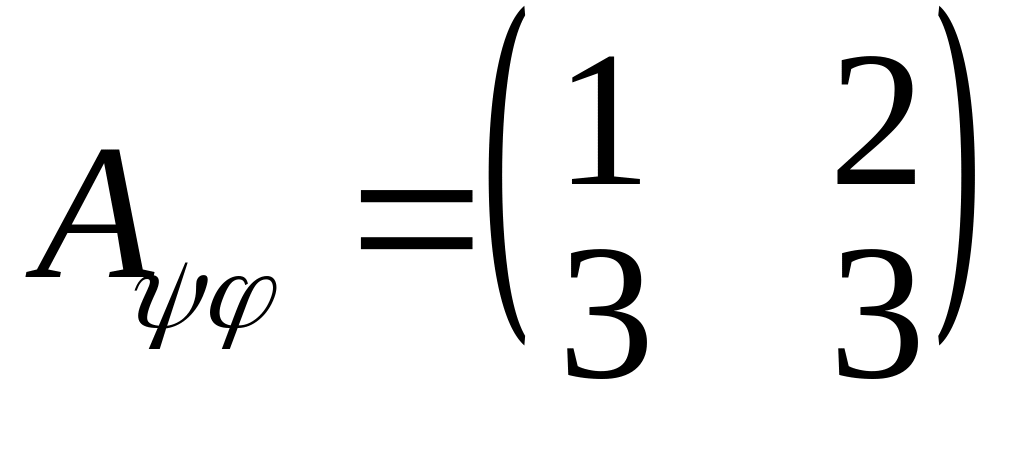 .
.
Матриця
![]() оператора
дорівнює добутку матриць операторів
і
,
тобто якщо
-
матриця оператора
в базисі
,
то
оператора
дорівнює добутку матриць операторів
і
,
тобто якщо
-
матриця оператора
в базисі
,
то
![]() .
Тоді маємо:
.
Тоді маємо:

Відповідь:
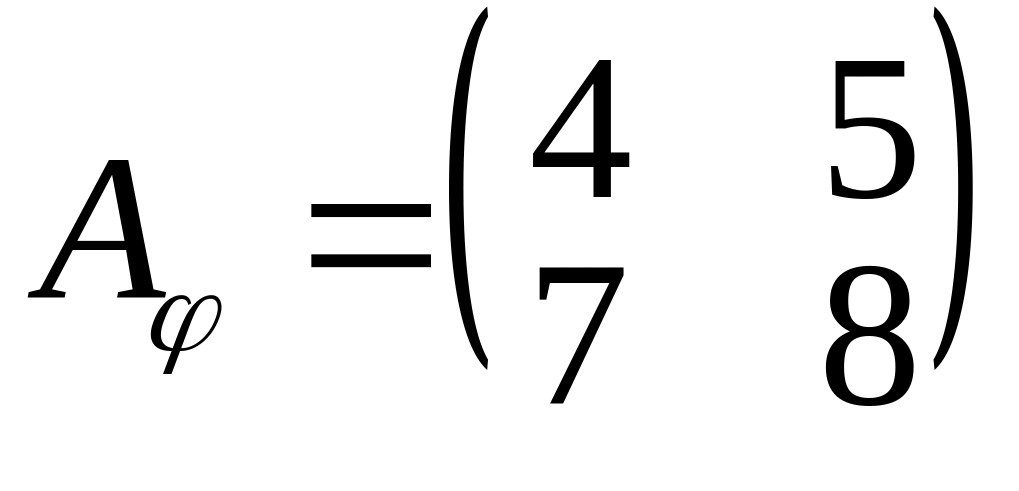 -
матриця оператора
в базисі
.
-
матриця оператора
в базисі
.
