4. Критерий минимаксного риска Сэвиджа

При применении этого критерия рассматривается матрица рисков | . Матрица рисков является преобразованной определенным образом платежной матрицей. Элементы матрицы рисков r_ji связаны с элементами матрицы полезности (выигрышей) следующим соотношением:

(в каждом столбце выбирается максимальный элемент, а затем из него вычитается соответствующий элемент столбца). Таким образом получается матрица рисков.

Далее в каждой строке выбирается максимальный элемент:

,. .

Это гарантированный результат при применении игроком той или иной стратегии, максимум, что игрок может потерять. Среди всех гарантированных результатов игрок будет выбирать ту стратегию, которая принесет ему минимальных проигрыш:

.

Оптимальной является та стратегия, которая принесет максимально возможный выигрыш при минимальном риске. Выбранная по данному критерию оптимальная стратегия совпадет с выбранной стратегией по критерию Вальда.

5. Критерий Ходжа-Лемана

Этот критерий опирается одновременно на минимаксный критерий (критерий Вальда) и критерий Лапласа. С помощью параметра γ выражается степень доверия к используемому распределений вероятностей. Если доверие велико, то доминирует критерий Лапласа, в противном случае - минимаксный критерий, т.е. мы ищем

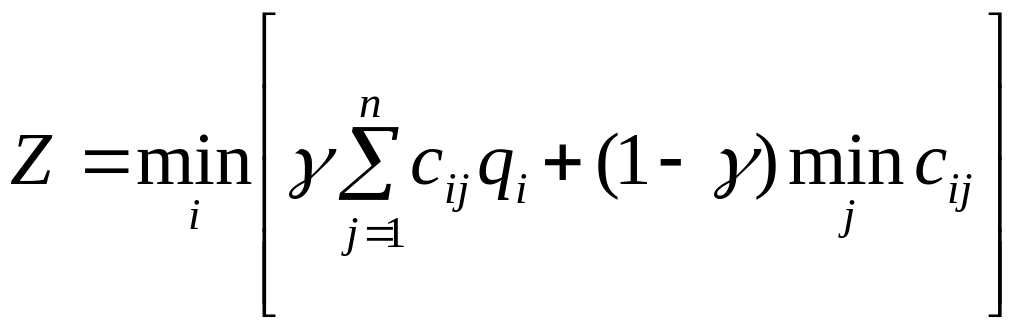, 0≤ γ ≤1

Правило выбора, соответствующее критерию Ходжа-Лемана, формируется следующим образом: матрица результатов дополняется столбцом, составленным из сумм средних взвешенных (с весом γ=const) математических ожиданий и наименьшего результата каждой строки. После этого в данном столбце отбирается вариант с наибольшим значением.

При γ = 1 критерий Ходжа-Лемана переходит в критерий Лапласа, а при γ = 0 становится минимаксным.

Выбор γ субъективен т.к. степень достоверности какой-либо функции распределения - дело тёмное.

6. Критерий Гермейера

Этот критерий ориентирован на величину потерь, т.е. на отрицательные значения матрицы С. При этом:

Правило выбора согласно критерию Гермейера формулируется следующим образом: матрица решений С дополняется ещё одним столбцом, содержащим в каждой строке наименьшее произведение имеющегося в ней результата на вероятность соответствующего состояния q_j, а затем выбирается вариант с наибольшим значением этого столбца.

Т.к. в хозяйственных задачах преимущественно имеют дело с ценами и затратами, условие обычно выполняется. В случае же, когда среди величин встречаются и положительные значения, можно перейти к строго отрицательным значениям с помощью преобразования - t при подходящем образом подобранном t > 0. При этом оптимальный вариант решения зависит от t.

7. Bl (mm) - критерий

Данный критерий является объединением критериев Лапласа и минимакса.

Правило выбора для этого критерия формулируется следующим образом: матрица решений С дополняется тремя столбцами. В первом из них записываются математические ожидания каждой из строк, во втором - разность между опорным значением и наименьшим значением соответствующей строки. В третьем столбце помещаются разности между наибольшим значением каждой строки и наибольшим значением той строки, в которой находится значение V₀. После этого выбираются те варианты, строки которых дают наибольшее математическое ожидание, а именно, соответствующее значение V₀ - из второго столбца должно быть равно некоторому заранее заданному уровню риска ξ_доп. Значение же из третьего столбца должно быть больше значения из второго столбца.