Задачи для самостоятельного решения.

Составив прямую и двойственную задачи линейного программирования решить задачи:

1. 2. 3.

4. 5. 6.

7. 8. 9.

10. 11. 12.

Принятие решений в условиях неопределенности. Игры с природой.

«Природа» может находиться в одном из множества возможных состояний, которое может быть как конечным, так и бесконечным. Будем считать, что множество состояний S_j конечно (j=1,…,m) или, по крайней мере, количество состояний можно пронумеровать. Все возможные состояния известны, не известно только, какое состояние будет иметь место в условиях, когда планируется реализация принимаемого управленческого решения. Будем считать, что множество управленческих решений (планов) A_i также конечно и равно n.

Допустим, каждому действию A_i и каждому возможному состоянию «природы» S_j соответствует результат (исход) , определяющий результат (выигрыш, полезность) при выборе i-го действия и реализации j-го состояния. Тогда платежная матрица будет иметь вид:

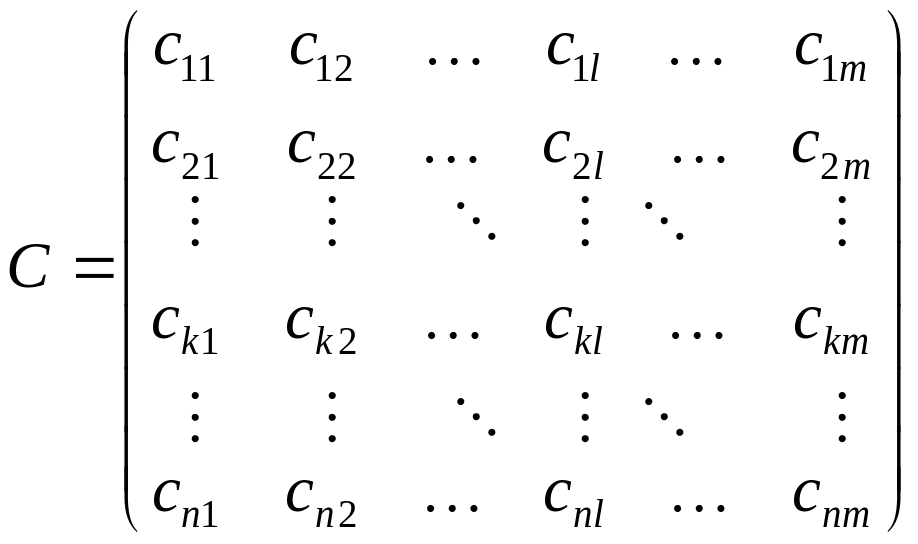
Для принятия решения в условиях неопределенности используется ряд критериев, среди которых: критерий Вальда, критерий Гурвица, критерий Сэвиджа, критерий Лапласа и др.

1. Критерий Вальда (критерий крайнего пессимизма).

Данный критерий опирается на принцип наибольшей осторожности и основывается на выборе наилучшей из наихудших стратегий. Тем самым выбранные варианты полностью исключают риск, т.е. принимающий решение не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Данный критерий не требует знания вероятностей состояний второго игрока и достаточно только матрицы.

В платежной матрице элемент представляет выигрыш (полезность) лица, принимающего решение. Сначала игрок выбирает минимальный элемент в стоке, что соответствует его гарантированному результату при применении этой стратегии:

для всех .

Далее, из всех своих гарантированных результатов он выбирает наилучший:

.

Таким образом, наилучшей стратегией будет та, которая в наихудших условиях принесет максимальный результат. Этот критерий применяется для развивающейся экономике на ранней стадии или в условиях кризисной ситуации.

2. Критерий максимакса. (критерий крайнего оптимизма).

Данный критерий основывается на предположении «все или ничего». В платежной матрице элемент представляет выигрыш (полезность) лица, принимающего решение. Сначала игрок выбирает максимальный элемент в стоке:

для всех .

Далее, из всех своих выбранных результатов он выбирает наилучший:

.

3. Критерий Гурвица (критерий пессимизма-оптимизма)

Данный критерий основан на следующих двух предположениях: «природа» может находиться в самом невыгодном состоянии с вероятностью k и в самом выгодном состоянии с вероятностью (1-k), где k – коэффициент пессимизма.

Критерий Гурвица устанавливает баланс между случаями крайнего пессимизма и крайнего оптимизма путем взвешивания обоих способов поведения соответствующими весами (1-k) и k, где 0 ≤k≤ 1.

Если в исходной задаче матрица возможных результатов представляет выигрыш, прибыль, полезность, доход и т.п., то критерий Гурвица записывается как:

, ,

тогда

Если , получим критерий Вальда, а если , то приходим к критерию максимакса.

В зависимости от значения коэффициента пессимизма критерий Гурвица применяется при различном состоянии экономики.