Задачи для самостоятельного решения.
Найти решение игры в чистых стратегиях:
1. 2. .3.
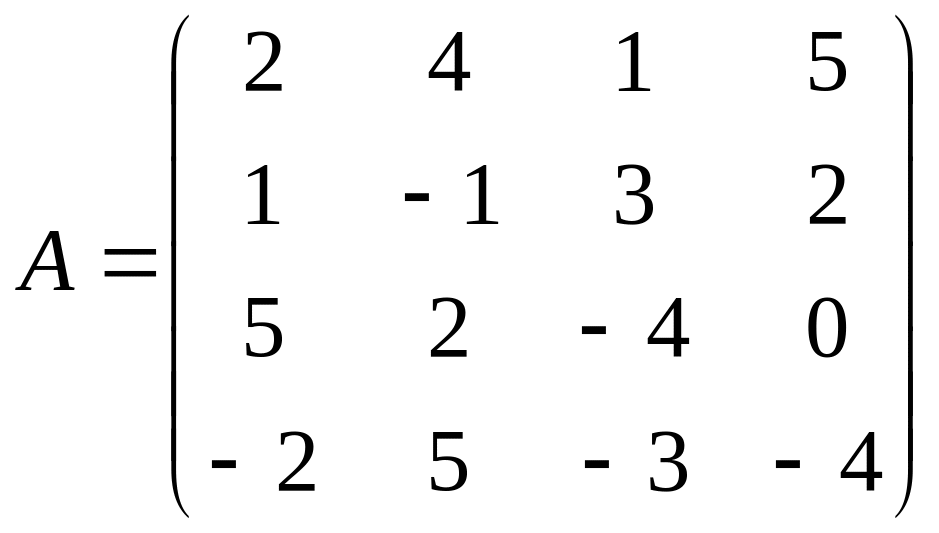
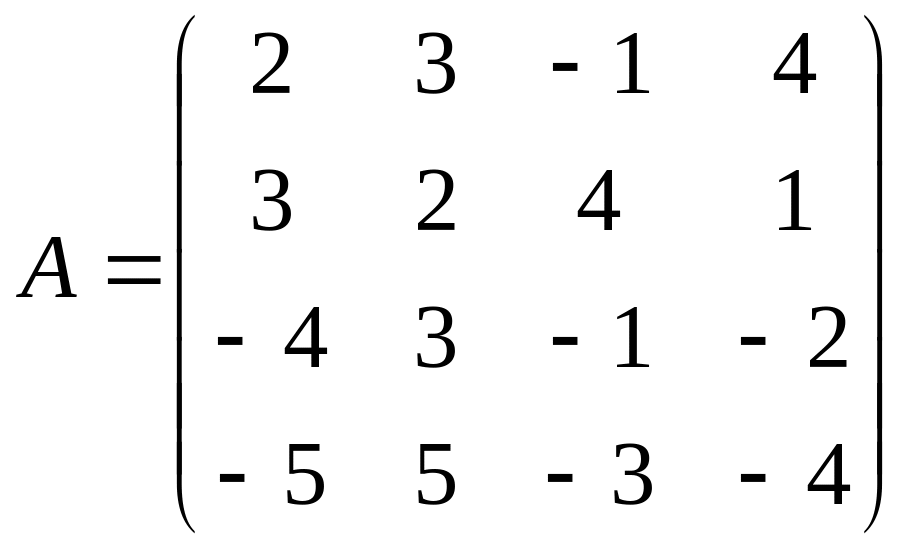
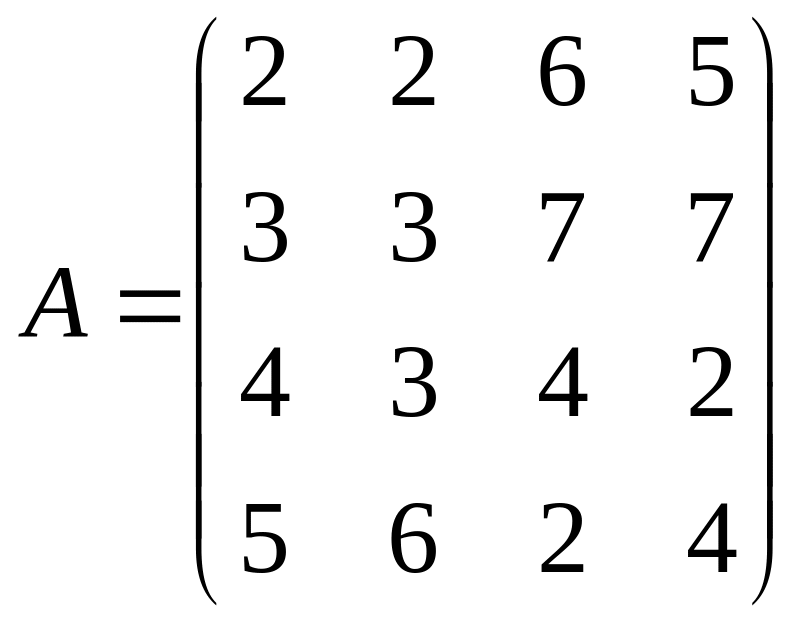
4. 5. 6.
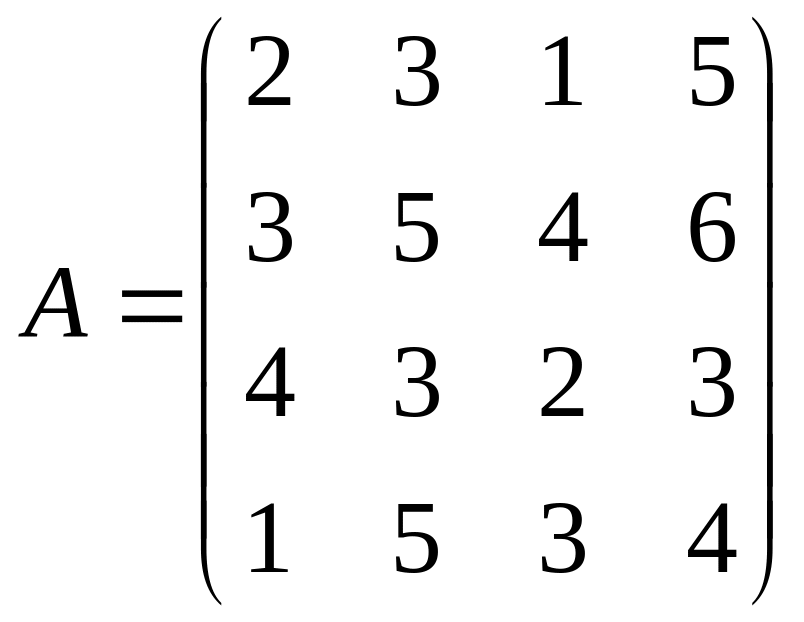
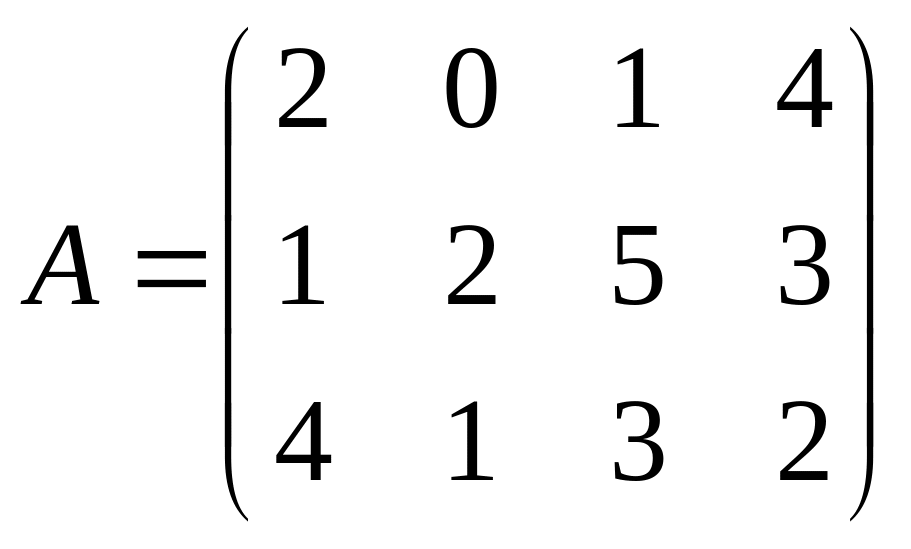
7. 8. 9.
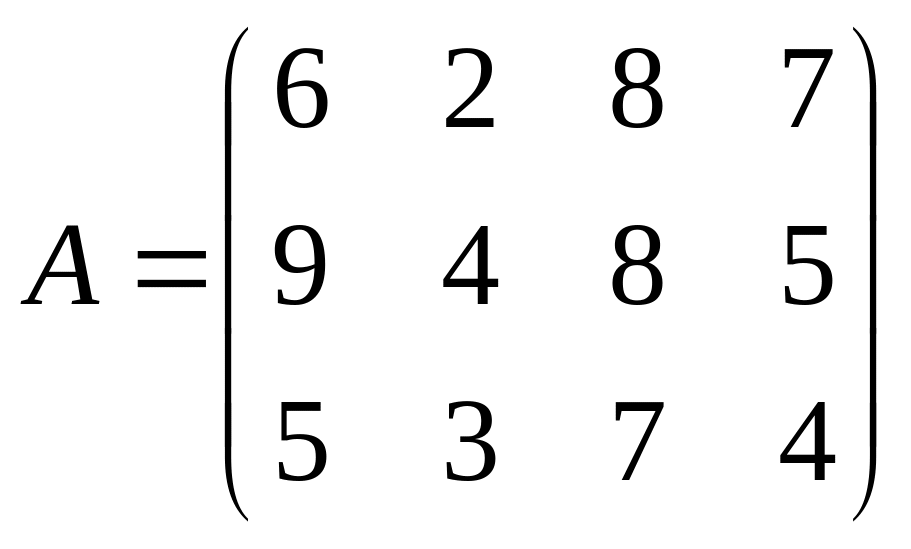
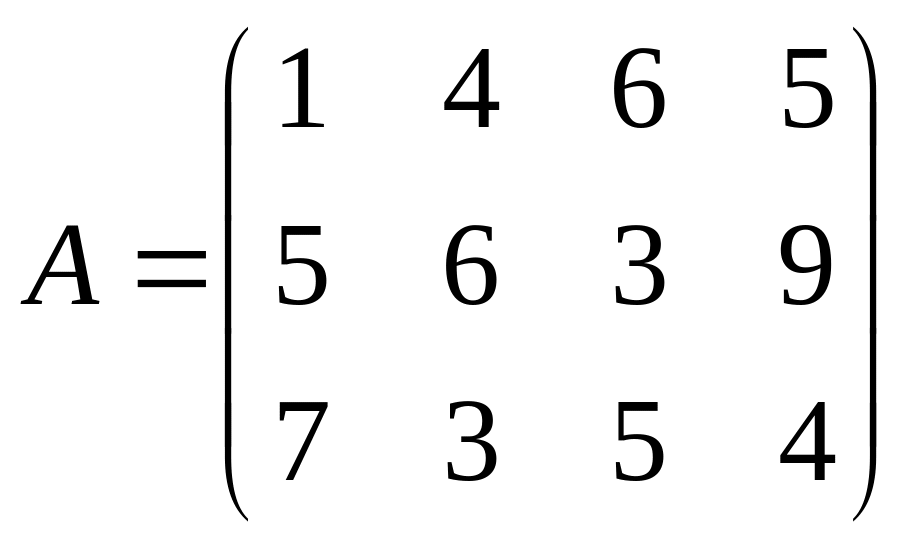
10. 11. 12.
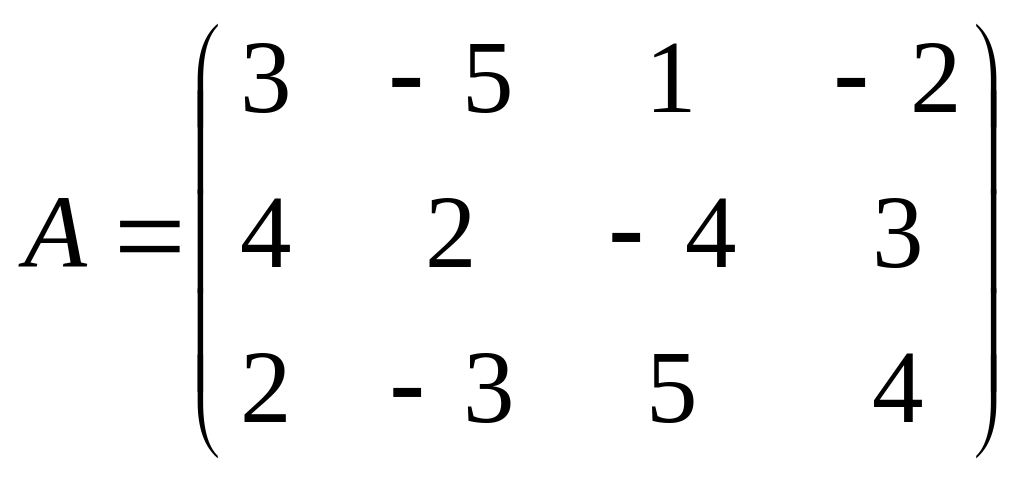
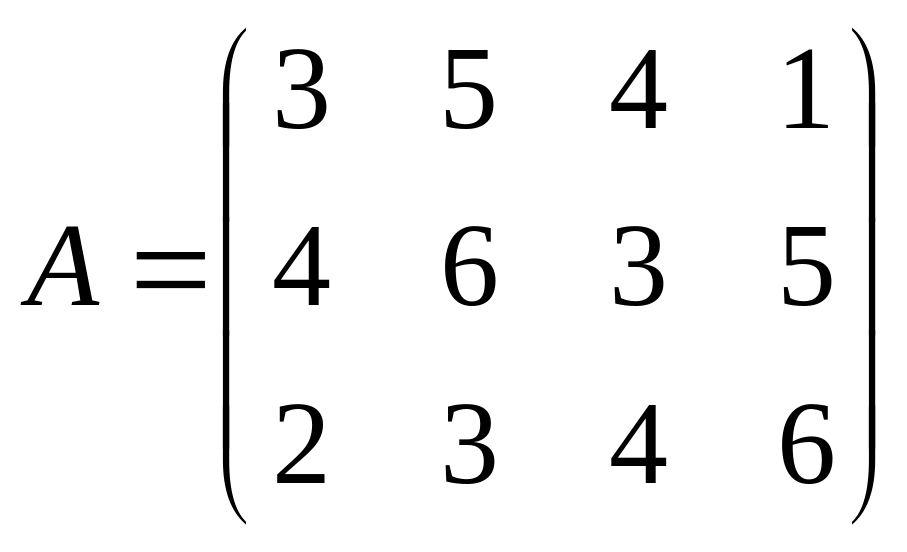
13. 14. 15.
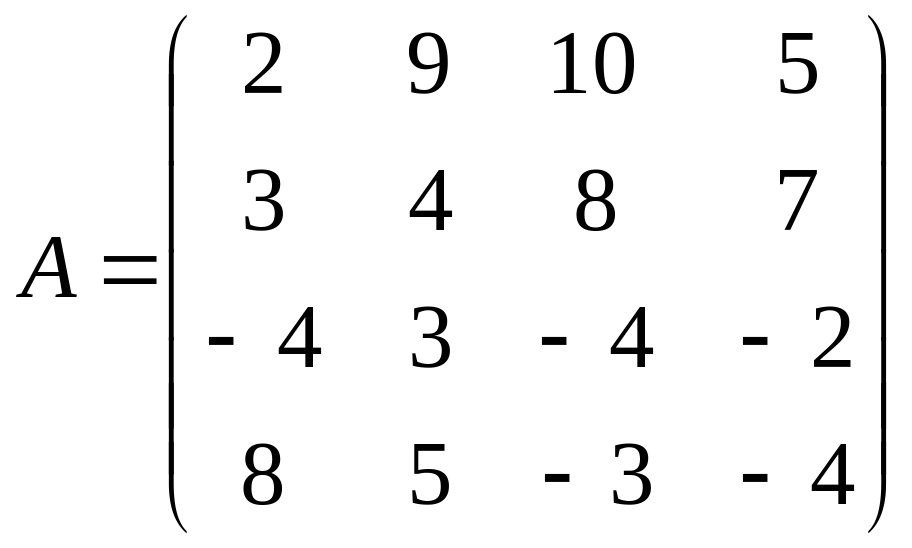
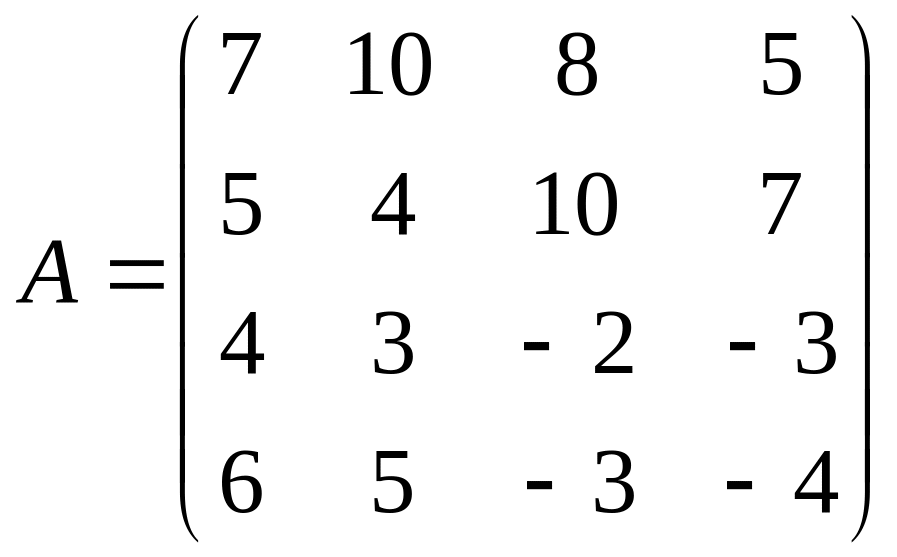
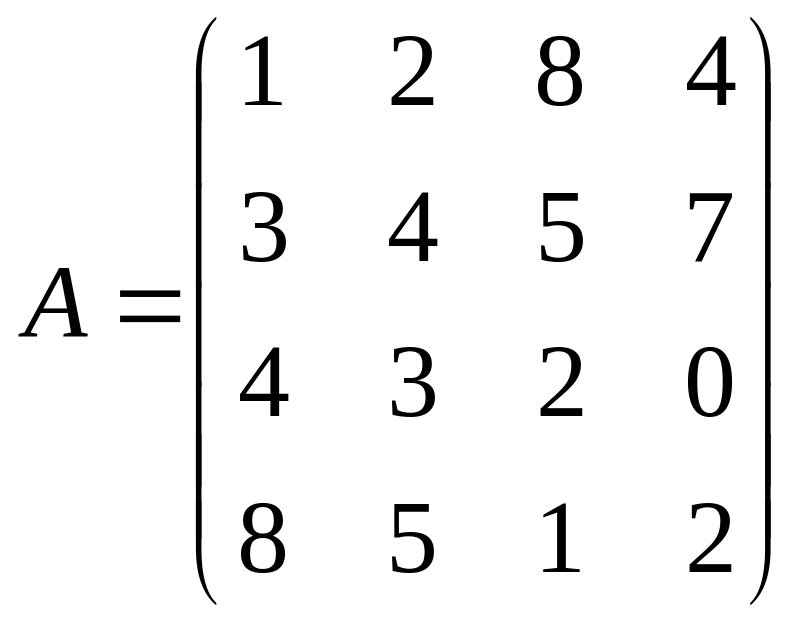
16. 17. 18.
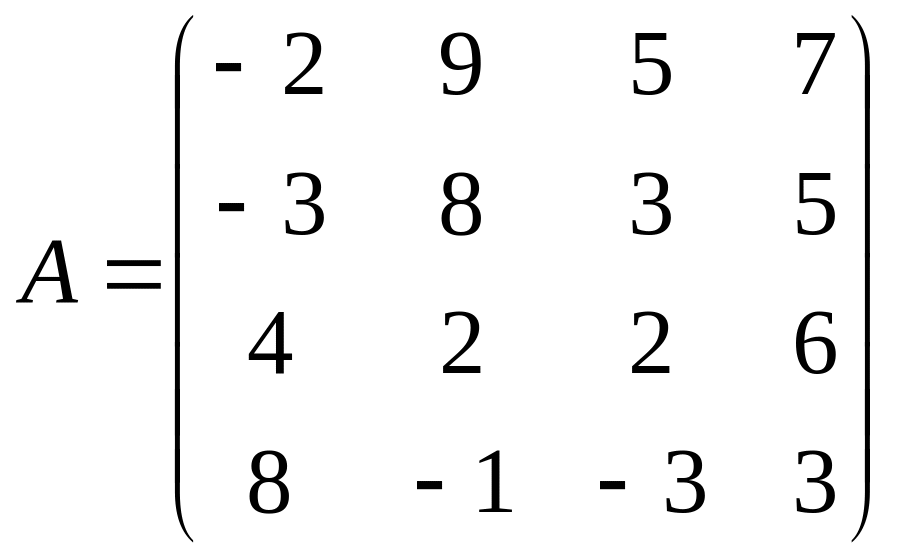
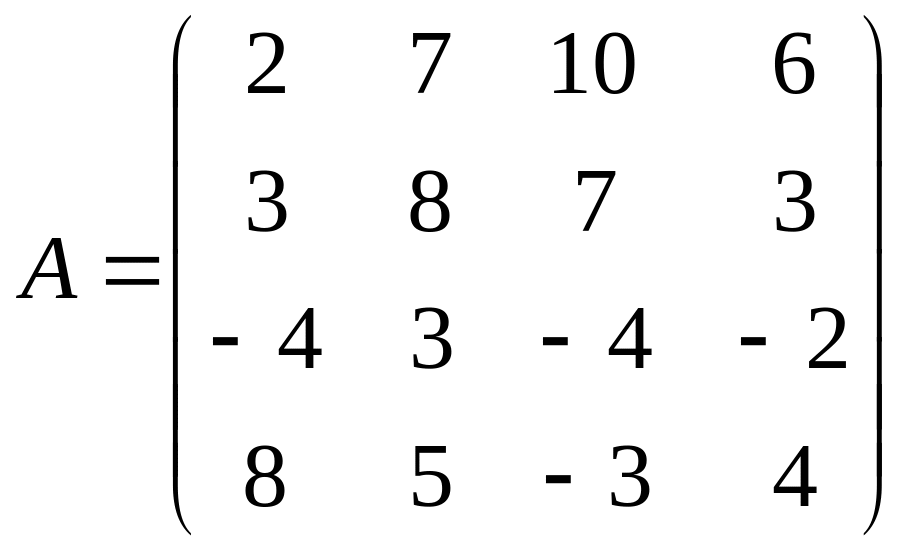
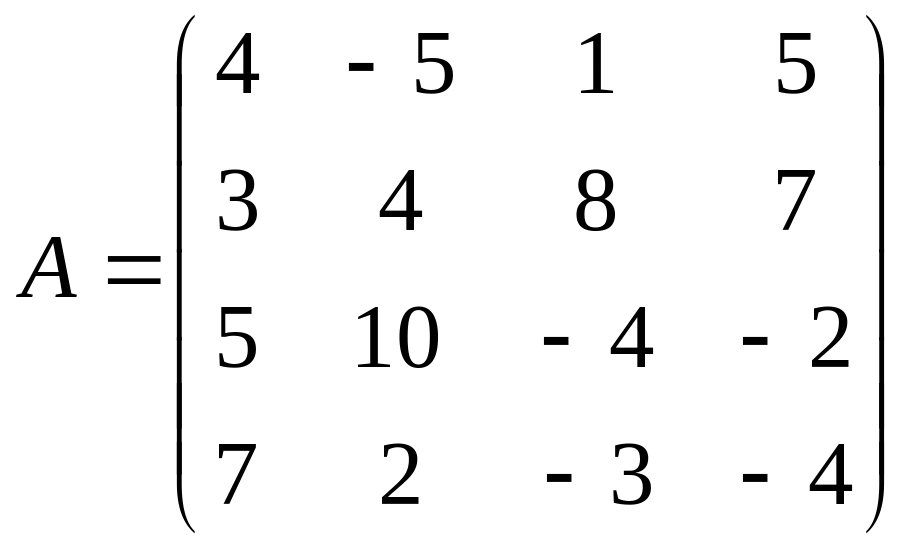
Антагонистические матричные игры с нулевой суммой имеющие решение в смешанных стратегиях.
К сожалению, решение игры в чистых стратегиях удается найти не так часто, как нам этого хотелось бы (это ведь совсем несложно сделать, и читатель уже в этом убедился). В таких случаях чистые стратегии уступают место смешанным.
Определение.
Смешанной стратегией игрока A
в игре Г
называется вероятность распределения
вектора
на множестве чистых стратегий
.
Вероятность
означает, что первый игрок выбирает
свою i-ю
стратегию с данной вероятностью. Вектор
удовлетворяет нормировочному условию
теории вероятностей
.
Определение.
Смешанной стратегией игрока B
в игре Г
называется вероятность распределения
вектора
на множестве чистых стратегий
.
Вероятность
означает, что первый игрок выбирает
свою j-ю
стратегию с данной вероятностью. Вектор
удовлетворяет нормировочному условию
теории вероятностей
.
Теорема (основная теорема матричных игр). Всякая матричная игра имеет решение в смешанных стратегиях.
Обозначим
через
- множество всех смешанных стратегий
первого игрока на множестве A.
Мы уже упоминали, что решение игры в
смешанных стратегиях существует только
тогда, когда не существует решение в
чистых стратегиях. Поэтому все вектора
p,
такие, что один элемент равен 1, а остальные
нулю, из множества
мы исключим, так как они равносильны
применением игроком чистой стратегии.
Аналогично, через
обозначим множество смешанных стратегий
второго игрока на множестве B
и так же исключим все единичные вектора.
Построим смешанное расширение антагонистической игры.
Определение. Антагонистическая игра
называется смешанным расширением игры Г.
Определение.
Решение
игры
называется решением
исходной игры Г
в смешанных стратегиях. При этом вектор
называется вектором
оптимальных смешанных стратегий игроков,
а
- выигрышем или значением игры и
выполняются условия:
,
для
.
Значение
игры является математическим ожиданием
выигрыша при применении игроками своих
оптимальных стратегий
.
Это значение легко найти, если известны
оптимальные значения векторов
распределения вероятностей. Но оптимальные
вектора тоже необходимо найти. Рассмотрим
различные методы решения матричных игр
в смешанных стратегиях.
Решение игр Решение игры 2х2
Самой простой игрой является игра, в которой каждый из двух игроков имеет по две стратегии. Тогда платежная матрица игры будет иметь две строки и два столбца.
|
|
|
|
|
|
|
|
|
Воспользуемся
определением решения игры. Рассмотрим
игру сначала с позиции первого игрока.
Пусть второй игрок применил свою
оптимальную стратегию, а первый – любую,
кроме оптимальной. Уже упоминалось, что
чистая стратегия не может быть оптимальной,
поэтому стратегии
и
нам подходят (они априори не могут быть
оптимальными). Воспользуемся левой
частью двойного неравенства и
математическим ожиданием выигрыша, не
забудем и про нормировочное условие.
Тогда получим систему из двух неравенств
и одного уравнения
,
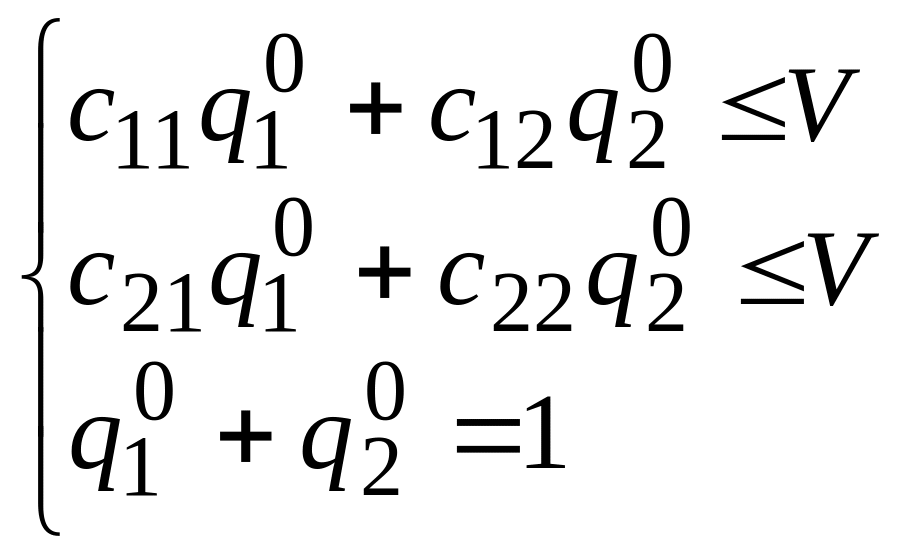где
,
То
есть умножим вектор
сначала на первую строку матрицы, а
затем на вторую. Первые два неравенства
системы всегда будут выполняться как
верные равенства. Тогда система примет
вид:
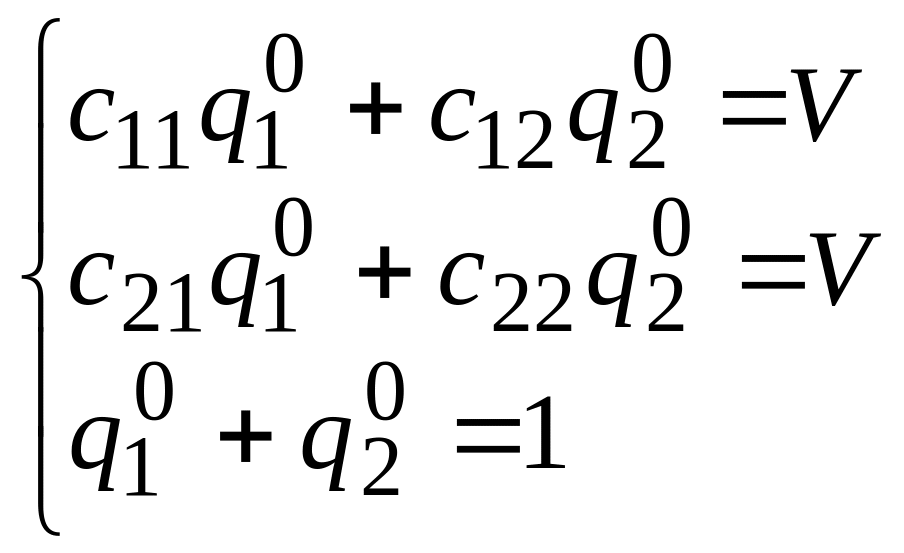
Вычтем второе уравнение из первого, приведем подобные и получим систему из двух уравнений с двумя переменными:
.
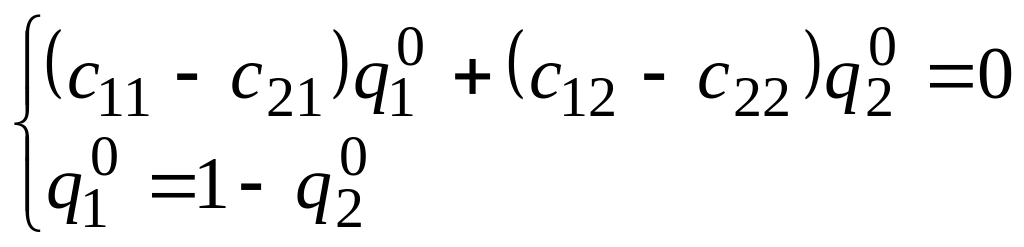Подставляя
в первое уравнение выраженное значение
для
,
получим уравнение:
,
приводя подобные, найдем выражение для
нахождения
:
,
.
Таким
образом, оптимальный вектор распределения
вероятностей найден и осталось только
найти выигрыш. Для этого необходимо
подставить значения вероятностей в
первое или второе уравнения системы.
Таким образом, решив данную систему,
найден вектор оптимального распределения
вероятностей второго игрока и выигрыш
Теперь
рассмотрим правую часть двойного
неравенства. Первый игрок применяет
свою оптимальную стратегию, а второй
любую, кроме оптимальной, например
чистые
и
.
Воспользуемся правой частью двойного
неравенства и математическим ожиданием
выигрыша, не забудем и про нормировочное
условие. Тогда получим систему из двух
неравенств и одного уравнения
,
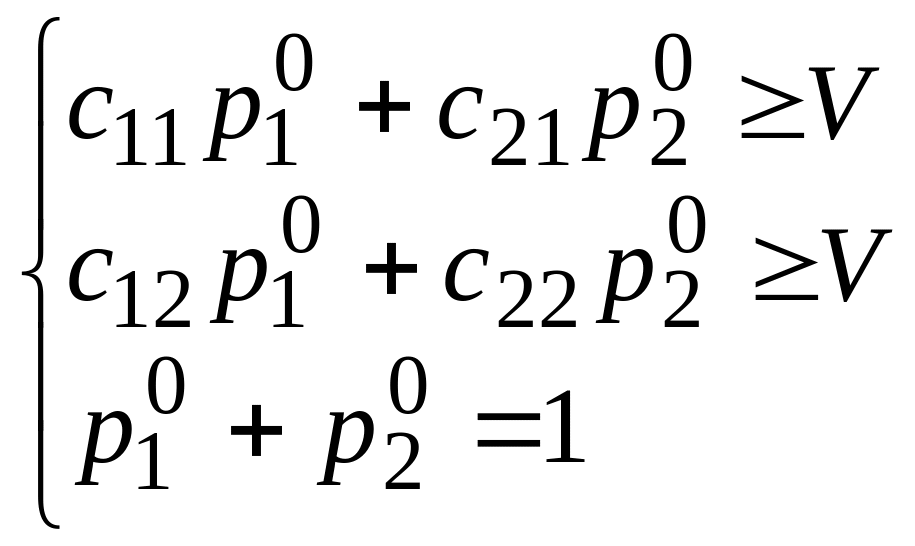где
,
на
этот раз умножаем вектор
на столбцы матрицы. Первые два неравенства
системы всегда будут выполняться как
верные равенства. Тогда система примет
вид:
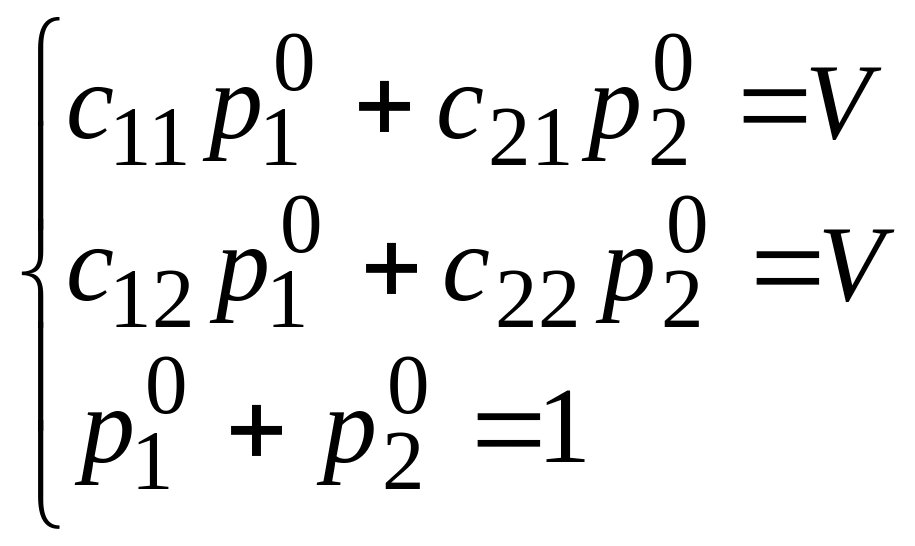
Вычтем второе уравнение из первого, приведем подобные и получим систему из двух уравнений с двумя переменными:
,
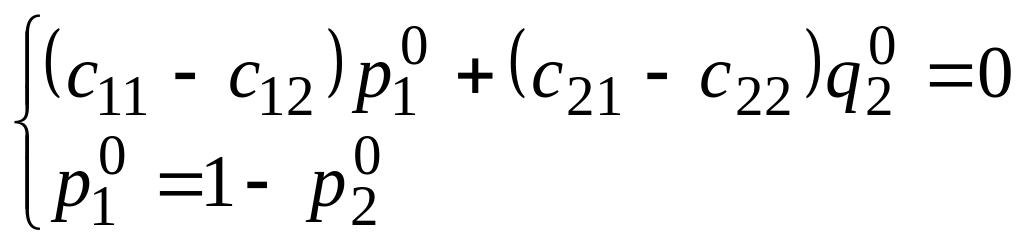Подставляя
в первое уравнение выраженное значение
для
получим уравнение:
,
приводя подобные, найдем выражение для
нахождения
:
,
.
Таким
образом, оптимальный вектор распределения
вероятностей первого игрока найден и
осталось только найти выигрыш. Для этого
надо подставить значения вероятностей
в первое или второе уравнение системы.
Таким образом, решив данную систему
найден вектор оптимального распределения
вероятностей второго игрока и выигрыш
Так как в условии в общем виде решения игры, когда оба игрока применяют свои оптимальные стратегии, одинаково, то и выигрыш при решении обоих систем должен быть одинаковым. Это условие и будет проверкой правильности решения задачи.
Пример. Найти решение игры 2х2
.
Решение.
Эта игра не имеет решение в чистых
стратегиях, так как
.
Значит, в соответствии с основной
теоремой матричных игр, она должна иметь
решение в смешанных стратегиях.
Рассуждения аналогичны решению задачи
в общем виде, поэтому они приводиться
еще раз не будут, запишем сразу системы:
.
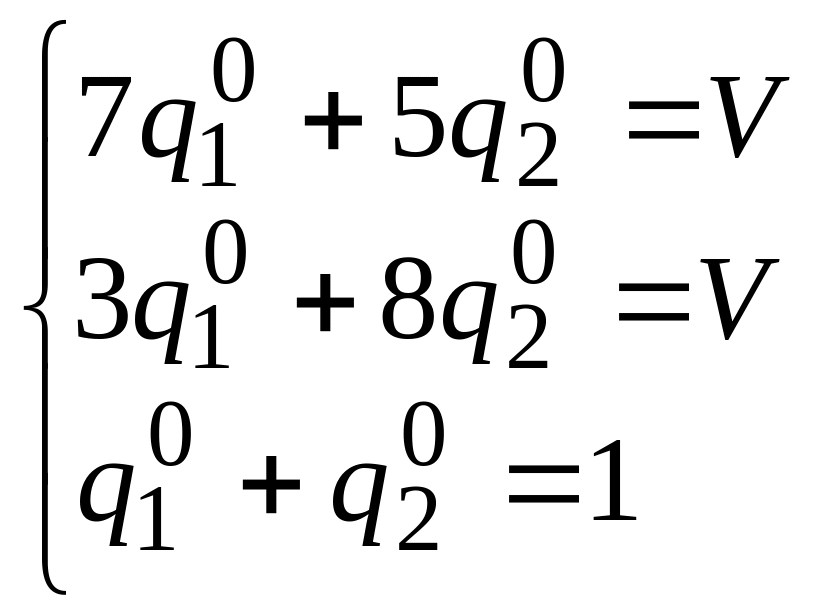
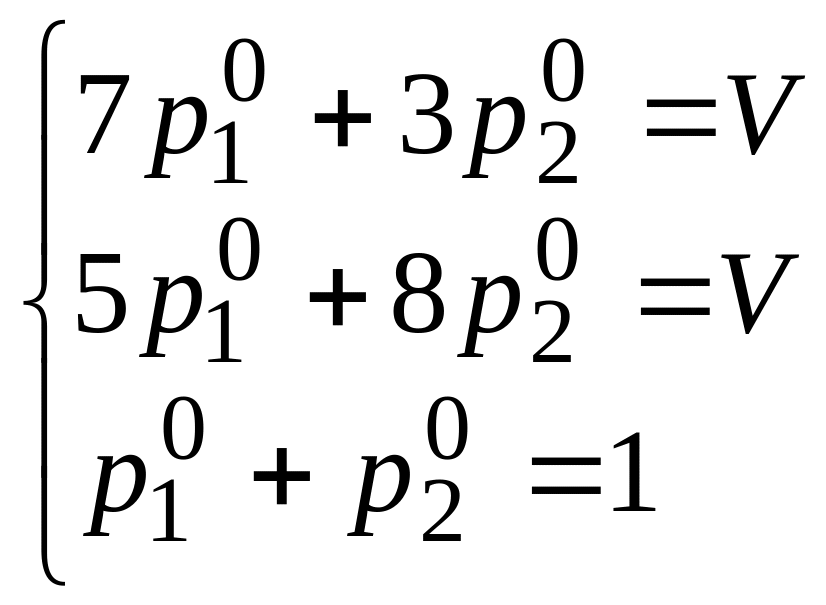Вычтем из первых строк вторые и приведем подобные:
.
Выигрыши в обоих случаях совпали, значит задача решена правильно.
Ответ:
.