Этапы синтеза на мультиплексорах.

1. Деминимизация функции (приведение к СДНФ)

2. Выбор аргументов подаваемых на адресные входы (на адресные входы подаются аргументы, которые чаще всего встречаются в минимизированном – исходном выражении)

3. Построение карт Карно с выделением областей, для которых выбранные переменные одинаковы.

4. Заносим в карту Карно единичные значения F(X…) деминимизированой функции.

5. Осуществляем минимизацию функции в нутрии выделенных областей.

6. Получаем минимизированную функцию для каждого набора на адресных шинах.

7. Составление структурной схемы.

Пример:

Синтезировать на мультиплексоре с двумя адресными входами логическую функцию пяти аргументов:

1. С помощью диминимизации функции приводим ее к виду СДНФ.

2. На адресные входы подаем аргументы, которые чаще всего встречаются в минимизированной формуле (исходной).

3. По функции полученной в результате деминимизации производим построение карт Карно: с выделением областей для которых выбранные переменные Х₁ и Х₂ одинаковы.

4. Осуществляем минимизацию функции в нутрии выделенных областей:

а) - область 00

Имеем два контура -

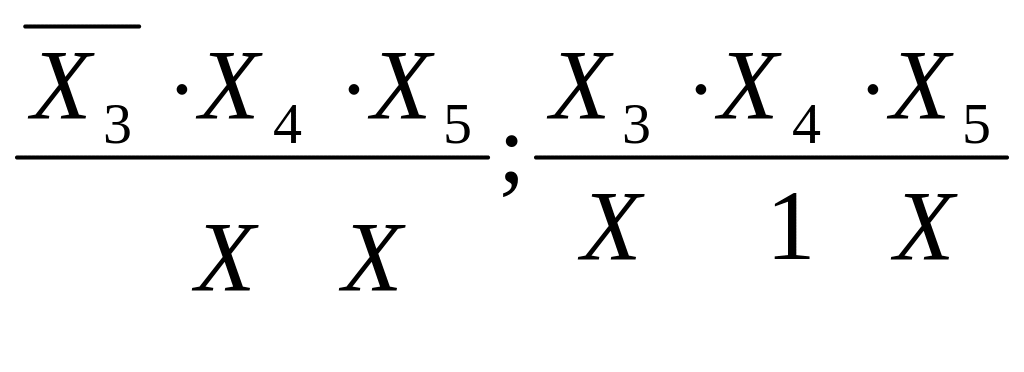
б) область

Имеем два контура -

в) Область

Имеем один контур -

г) Область

Теперь приступаем к составлению схемы для данной логической функции:

Универсальные логические элементы.

1. Мультиплексоры.

2. Демультиплексоры.

3. Программируемые логические матрицы (ПЛМ).

4. Программируемая матричная логика (ПМЛ).

5. Программируемые матричные вентили (ПМВ).

6. ПЗУ.

Демультиплексор (дешифратор) – определяется как микросхема, у которой N входов и 2^N – выходов. На входы подают всевозможные наборы Х₁, Х₂…Х_N, а на одном из 2^N выходов появляется единица на остальных выходах 0.

Такой дешифратор реализует 2^N функции вида

Легко заметить, что дешифратор реализует всевозможные константные единицы, которые можно образовать от N переменных.

Следовательно, построение комбинационных устройств с использованием дешифраторов сводится к объединению с помощью элементов ИЛИ тех выходов Di, которые соответствуют константам единицы заданной функции.

Пример:

	D0	D1	D2	D3	D4	D5	D6	D7
X1	0	0	0	0	1	1	1	1
X2	0	0	1	1	0	0	1	1
X3	0	1	0	1	0	1	0	1
F1	0	1	1	0	1	0	0	1
F2	0	0	0	1	0	1	1	1

При использовании мультиплексоров для каждой функции требуется отдельный мультиплексор. В противоположность этому выходы одного дешифратора могут быть использованы для формирования большого числа функций, зависящих от одних и тех же аргументов.

При использовании дешифраторов ни одна из конституентных единиц не подвергается операции инвертирования, даже если среди них есть соседние.

Поэтому в тех случаях, когда в таблице истинности функции f(x) число единиц больше числа нулей, для упрощения схемных построений целесообразно реализовывать инверсию функции , так как для этого понадобится элемент ИЛИ с меньшим числом входов. При использовании элементов ИЛИ-НЕ может быть сразу получена функция f(x).

Если число переменных меньше числа входов дешифратора N > m, то на N - m неиспользуемых входов дешифратора формирует лишь те коституенты единицы, двоичные номера которых содержат, заданны, таким образом, наборы из N – m констант.

Если же число входов дешифратора меньше числа переменных функции, то можно получить составной дешифратор на m входов.

Метод минимизации переключательных функций, использованный нами при использовании дешифраторов теряют смысл. Более того, если реализуемые функции заданы минимизированными, то необходимо их привести к совершенно дизъюнктивной нормальной форме.