13. Конформные отображения

Определение 3.8.

Отображение называется конформным и точке , если оно сохраняет углы между кривыми и обладает свойством постоянства растяжений в точке по всем направлениям, выходящим из точки .

Таким образом, на основании результатом предыдущего параграфа мы приходим к следующей теореме.

Теорема 3.9.

Если функция аналитическая в точке и , то отображение является конформным и точке .

Определение 3.9.

Функция называется однолистной и области , если для любых из .

Пример 1.

Функция не является однолистной на всей комплексной плоскости, так как для и выполняется условие

Определение 3.10.

Отображение называется конформным и области , если оно конформно в каждой точке области и функция является аналитической и однолистной и области .

Докажем следующую теорему.

Теорема 3.10.

Пусть функция – однолистная и аналитическая в области и в каждой точке области . Тогда отображение будет конформным в области .

Доказательство.

В силу условия при и теоремы 3.9. отображение, осуществляемое функцией , является конформным в каждой точке области .

А следовательно, отображение будет конформным в области , так как выполняются все условия определения 3.10.

Таким образом мы доказали, что условия аналитичности, однолистность и неравенство нулю производной функции является достаточными условиями конформности отображения, осуществляемого этой функцией.

14. Линейная функция

Линейной называется функция , где и – комплексные постоянные, .

Линейная функция обладает следующими свойствами.

1. Областью определения функции является вся комплексная плоскость.

1. Линейная функция принимает любое комплексное значение. В самом деле, уравнение разрешимо относительно при любом , .

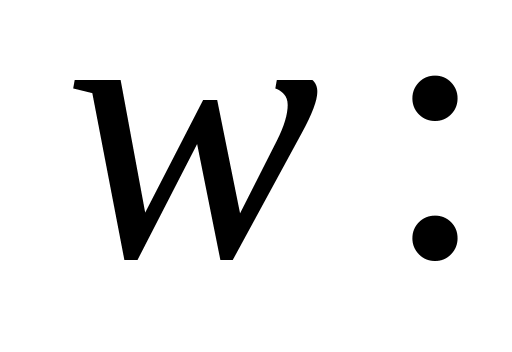
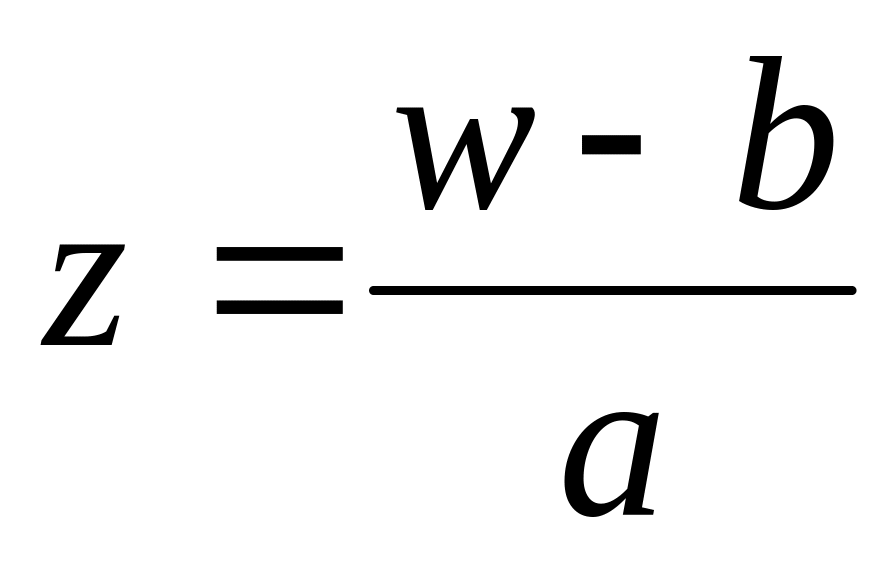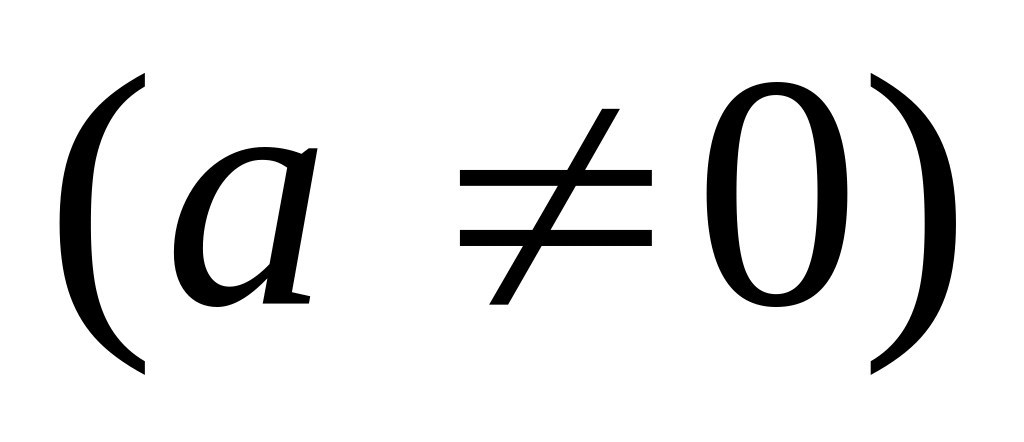2. Отображение однолистно на всей комплексной плоскости, так как 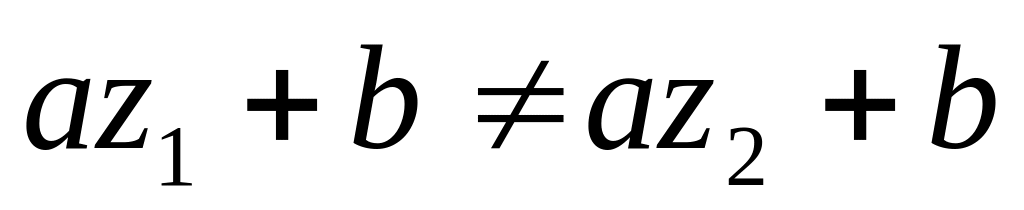, если для 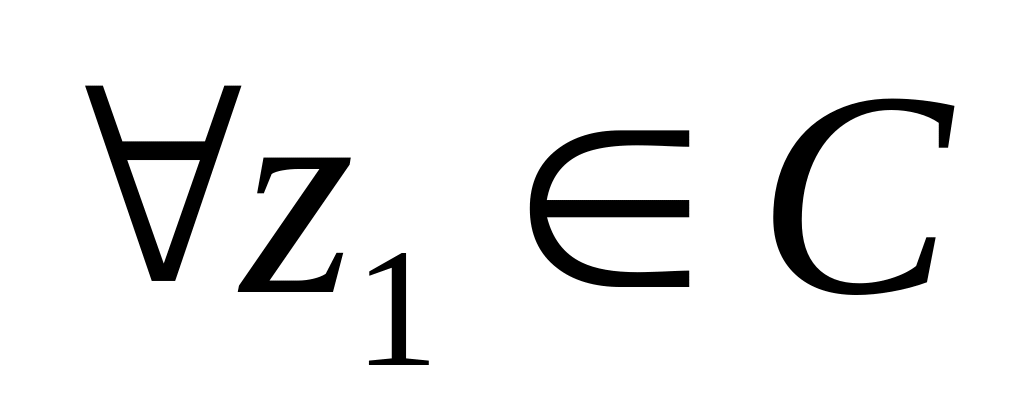и .

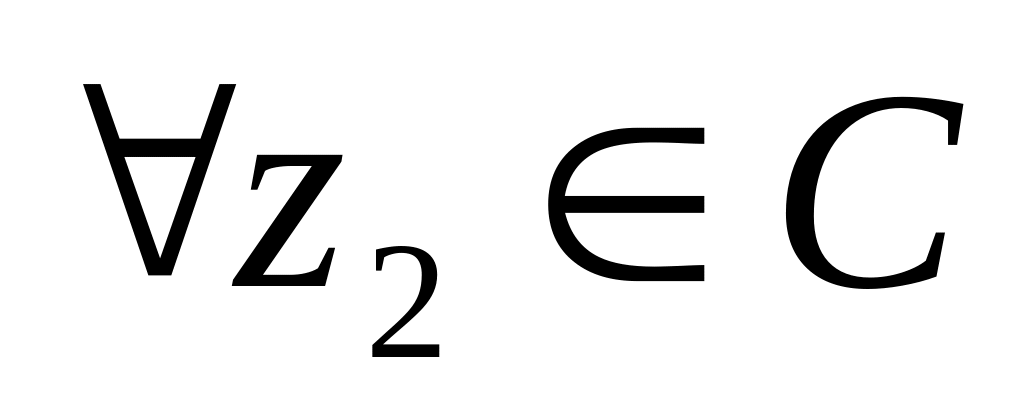4. Заметим, что .

Доопределим линейную функцию на бесконочности

Тогда функция определена на расширенной комплексной плоскости.

5. Производная линейной функции ранни

.

Функция , следовательно, аналитична по всей комплексной плоскости.

6. Из свойств 3, 5 и теоремы 3.10. следует, что линейная функция осуществляет конформное отображение комплектной плоскости на себя.

Чтобы подробнее изучить отображение, осуществляемое линейной функцией, рассмотрим вначале частные случаи. Будем изображать и точками одной и той же плоскости.

1. Пусть . Тогда (рис.4 1).

Заметим, что преобразование плоскости и этом случае сводится к параллельному переносу с вектором переноса . В самом деле, полагая , , , получим

,

откуда , .

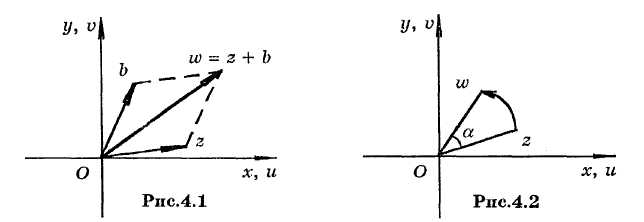
Мы получили формулы параллельного переноса в декартовых координатах.

Если точка опишет некоторую кривую, то преобразование только перенесет её в направлении вектора , так как каждая точка кривой перемещается по прямой, параллельной вектору на одно и тоже расстояние равное .

2. Пусть , т.е. , . Тогда . (4.2)

Из (4.2) имеем: , , так как . Из этих равенств следует, что точка получается из точки поворотом вектора вокруг начала координат на угол (рис.4.2).

Действительно,

Так что: , .

Мы получили известные формулы поворота осей координат.

3. Пусть ( – действительное положительное число), . В этом случае . (4.3)

Из (4.3) имеем , .

Таким образом, точка и соответствующая точка находятся на одном и том же луче, выходящем из начала координат, отношение расстояния от начала координат до точки к расстоянию от начала координат до точки постоянно и равно , т.е. преобразование является гомотетией с центром в точке и коэффициентом .

При имеем растяжение, имеем сжатие, при имеем тождественное преобразование плоскости на себя (рис.4.3).

Р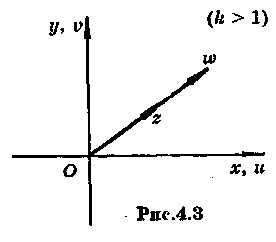 ассмотрим теперь отображение с помощью любой линейной функции .

Полагая ,получим . (4.4)

Преобразование (4.4) есть суперпозиция преобразований

, ,

Поэтому переход от точки к точке можно осуществлять, выполнив в укапанном порядке следующие преобразования:

1) поворот вектора относительно начала координат на угол ,

2) преобразование гомотетии с центром в начале координат и коэффициентом ,

3) параллельный перенос полученной точки на вектор .