
- •1. Комплексные числа
- •2. Геометрическая интерпретация комплексных чисел и основных операций над ними
- •3. Тригонометрическая и показательная форма комплексного числа
- •4. Комплексной функции комплексного переменного
- •5. Действительная и мнимая части комплексной функции
- •6. Метризация комплексной плоскости. Последовательности комплексных чисел и их пределы
- •7. Предел комплексных функций
- •8.Непрерывность комплексных функций
- •9. Моногенность комплексных функций
- •10. Производная
- •11. Аналитические функции
- •12. Геометрический смысл модуля и аргумента производной
- •13. Конформные отображения
- •14. Линейная функция
- •15. Степенная функция с натуральным показателем
- •16. Показательная функция
- •17. Отображения, осуществляемые показательной функцией
- •18. Тригонометрические функции комплексного переменного
- •19. Гиперболические функции комплексного переменного
- •20. Логарифмическая функция комплексного переменного
- •21. Обратные тригонометрические функции
- •22. Интегрирование комплексных функций
- •Если интегрирование по замкнутой кривой проводится в направлении противоположном рассматриваемому ("по часовой стрелке") , то для обозначения интеграла употребляют символы.
- •23. Теорема Коши для односвязной области
- •24. Первообразная. Аналог формулы Ньютона-Лейбница для комплексных функций
- •25. Теорема Коши для многосвязной области
- •26. Формула Коши
- •27. Бесконечная дифференцируемость аналитической функции
- •28. Теорема Лиувилля. Основная теорема алгебры
- •30. Числовые комплексные ряды
- •31. Функциональные комплексные ряды
- •32. Степенные комплексные ряды
- •33. Разложение аналитической функции в степенной ряд Тейлора
5. Действительная и мнимая части комплексной функции
Комплексная
функция
каждому
![]() ставит
в соответствие единственное комплексное
число
ставит
в соответствие единственное комплексное
число
![]() .
.
(![]() и
и
![]() здесь
и дальше область определения, множество
значений
функций
соответственно), другими словами каждой
паре
действительных чисел
ставится
в соответствие пара действительных
чисел
здесь
и дальше область определения, множество
значений
функций
соответственно), другими словами каждой
паре
действительных чисел
ставится
в соответствие пара действительных
чисел
![]() .
Очевидно
последнее соответствие можно
представить как две действительные
функции двух действительных
переменных
,
так как каждой паре
ставится
в соответствие действительное число
.
Очевидно
последнее соответствие можно
представить как две действительные
функции двух действительных
переменных
,
так как каждой паре
ставится
в соответствие действительное число
![]() и
действительное число
v.
и
действительное число
v.
Как известно из теории действительных функций многих действительных переменных такие функции называются действительными функциями двух действительных переменных:
![]() ;
;
![]() .
.
Теперь комплексную функцию , учитывая, что , , можно представить в виде
![]()
или ![]() .
.
Действительную функцию называют действительной частью комплексной функции , а функцию — мнимой частью функции и обозначают:
![]() ,
,
![]() .
.
В дальнейшем вместо
и будем употреблять также запись :
![]() и
и
![]() .
.
Пример 1.
Найти действительную и мнимые части комплексной функции .
Решение.
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() — действительная
часть функции
,
— действительная
часть функции
,
![]() —
мнимая
часть этой функции.
—
мнимая
часть этой функции.
Замечание.
Если
заданы две действительные функции двух
действительных переменных
,
на некотором
множестве
![]() ,
то
функция
,
то
функция
![]() будет
комплексной функцией комплексного
переменного
.
будет
комплексной функцией комплексного
переменного
.
Пример 2.
![]() ;
;
![]() .
.
— любая точка координатной плоскости.
Функция
![]() — комплексная функция
комплексного переменного
,
заданная
во всей комплексной плоскости. (Здесь
и дальше фраза: "функция
задана на множестве
— комплексная функция
комплексного переменного
,
заданная
во всей комплексной плоскости. (Здесь
и дальше фраза: "функция
задана на множестве
![]() "
означает,
что множество
или
совпадает с областью определения
функции
или принадлежит этой области).
"
означает,
что множество
или
совпадает с областью определения
функции
или принадлежит этой области).
6. Метризация комплексной плоскости. Последовательности комплексных чисел и их пределы
Введем на множестве комплексных чисел (комплексной плоскости) расстояние между любыми двумя комплексными числами , (точками комплексной плоскости , ) по формуле
![]() .
.
(Символ
![]() означает расстояние между
,
).
означает расстояние между
,
).
Легко проверить, используя свойства модуля, что так определенное "расстояние" удовлетворяет всем аксиомам расстояния:
1.
![]() ; 2.
; 2.
![]() ;
;
3.
![]()
(Эти аксиомы можно получить из геометрических соображений, если помнить, что модуль разности 2-х комплексных чисел равен расстоянию между точками, изображающими эти числа).
Введя понятие расстояния на множестве комплексных чисел мы это множество метризовали, а в любом метрическом пространстве можно строить теорию пределов для последовательностей элементов этого пространства.
Так как понятие расстояния на множестве комплексных чисел вводится также как и на множестве действительных чисел, и именно как модуль разности двух чисел, то с формальной стороны определения, теоремы и их доказательства в случае комплексных чисел выглядят также как и в случае действительных чисел.
Определение 2.2.
Комплексное
число
![]() называется пределом последовательности
комплексных чисел
,
,
называется пределом последовательности
комплексных чисел
,
,![]() ,
,![]() ,
,
если для
,
,
если для
![]() ,
,
![]() ,
что для
,
что для
![]() .
.
Обозначение
![]() .
.
Формулировку теорем и их доказательство для комплексных последовательностей приводить не будем, но результатами известными из теории последовательностей действительных чисел пользоваться будем (теоремы о пределе суммы, произведения, о единственности предела и т.д.).
Сформулируем и докажем полезную для дальнейшего теорему.
Теорема 2.1.
Если
последовательность комплексных чисел
![]()
![]() ,
,
![]() сходится к комплексному числу
,
то сходятся
действительные последовательности
сходится к комплексному числу
,
то сходятся
действительные последовательности
![]() ,
,
![]() ,
,
![]() ,
,
![]() и
наоборот.
и
наоборот.
Доказательство.
1.
![]() для
для
,
,
![]()
![]() .
.
Но
![]() и
и
![]()
![]() ;
;
![]()
Первая часть теоремы доказана.
2.
Дано:
![]() ,
,
![]()
Значит,
для любого
![]() ,
что
,
что
![]() для
для
![]() и
и
![]() ,
что
,
что
![]()
![]() .
.
Ho
![]() ,
если
,
если
![]() ,
т.е.
,
т.е.
![]() .
Что и
требовалось
доказать.
.
Что и
требовалось
доказать.
Справедлив
также критерий Коши: для того чтобы
последовательность
![]() была
сходящейся, необходимо и достаточно,
чтобы она была фундаментальной, т.е. для
любого
была
сходящейся, необходимо и достаточно,
чтобы она была фундаментальной, т.е. для
любого
![]() ,
должен существовать такой номер
,
должен существовать такой номер
![]() ,
что при
,
что при
![]() ,
,
![]() выполняется
неравенство
выполняется
неравенство
![]() .
С доказательством критерия Коши
можно познакомиться в [1].
.
С доказательством критерия Коши
можно познакомиться в [1].
Из
теоремы 2.1. следует, что сходящаяся
последовательность ограничена,
т.е. существует такое число
![]() ,
что
,
что
![]() для любого
.
Действительно, пусть последовательность
для любого
.
Действительно, пусть последовательность
![]() сходится.
Согласно теореме 2.1. действительные
последовательности
и
также
сходятся, а, следовательно, они ограничены,
т.е. при любых
имеют
место неравенства
сходится.
Согласно теореме 2.1. действительные
последовательности
и
также
сходятся, а, следовательно, они ограничены,
т.е. при любых
имеют
место неравенства
![]() ,
,
![]() ,
где
,
где
![]() —
некоторое неотрицательное
число.
—
некоторое неотрицательное
число.
Тогда
из неравенства
![]() следует,
что
,
при
любом
,
что и означает ограниченность
последовательности
.
Простейший
пример
следует,
что
,
при
любом
,
что и означает ограниченность
последовательности
.
Простейший
пример
![]() показывает, что ограниченная
последовательность не всегда сходится.
Но справедлива следующая теорема.
показывает, что ограниченная
последовательность не всегда сходится.
Но справедлива следующая теорема.
Теорема 2.2. (теорема Болъцано-Вейерштрасса).
Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Доказательство.
Пусть последовательность ограничена, т.е. для любого имеет место неравенство , где — некоторое неотрицательное число. Тогда из неравенств
![]() ;
;
![]()
следует,
что
![]() ;
;
![]() для
любого
что
означает
ограниченность действительных
последовательностей
и
.
Для
ограниченных действительных
последовательностей
,
теорема Больцано-Вейерштрасса верна.
Следовательно,из
них можно выделить сходящиеся
подпоследовательности, соответственно
для
любого
что
означает
ограниченность действительных
последовательностей
и
.
Для
ограниченных действительных
последовательностей
,
теорема Больцано-Вейерштрасса верна.
Следовательно,из
них можно выделить сходящиеся
подпоследовательности, соответственно
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Согласно
теореме 2.1.,
![]() ,
т.е.
,
т.е.
![]() подпоследовательность
подпоследовательность
![]() .
.
Теорема доказана.
Теорема 2.3.
Если
![]() ,
то последовательность
,
то последовательность
![]() сходится к пределу
сходится к пределу
![]() и существует последовательность из
значений
и существует последовательность из
значений
![]() :
:
![]() ,
,
![]() ,
,
,
,![]() ,
,
,
,
сходящаяся к одному из значений аргумента предела . (Здесь и в дальнейшем символ означает одно из значений аргумента числа ).
Доказательство.
П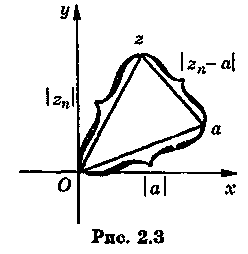 усть
существует
.
Тогда
усть
существует
.
Тогда
![]() для
.
для
.
Но
![]() .
.
Этот
факт геометрически очевиден, если
числа
и
изобразить на плоскости
(рис. 2.3). Значит
![]() для
так
как
.
Следовательно
.
для
так
как
.
Следовательно
.
Остальные утверждения теоремы принимаем без доказательства. Их доказательство смотри в [2].
