4. Комплексной функции комплексного переменного

Определение 2.1

Функция называется комплексной функцией комплексного переменного, если область определения и множество значений функции f есть некоторые множества комплексных чисел.

Пример 1.

, n — натуральное.

Для обозначения комплексной функции в дальнейшем будем применять символ ( — независимая переменная; — зависимая переменная). Область определения этой функции — все множество комплексных чисел, так как любое комплексное число можно возвести в п-ую степень. Кроме этого, легко показать, что функция принимает любое комплексное значение , что равносильно утверждению: уравнение разрешимо относительно при любом комплексном . Пусть , , где , , , , тогда

Из последнего равенства имеем:

Отсюда имеем

.

, .

Итак, решения уравнения найдены при любом комплексном и эти решения определяются формулой

, ,

.

При решение уравнения очевидно: .

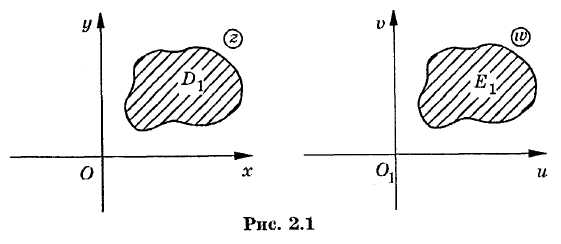
Р ассмотрим две комплексные плоскости (рис. 2.1). Первую плоскость будем обозначать символом , а вторую — .. Комплексные числа, соответствующие точкам плоскости будем обозначать так , a комплексные числа, соответствующие точкам плоскости , обозначим следующим образом

.

И зобразим на комплексной плоскости область определения функции f — множество , а на комплексной плоскости изобразим множество значений этой функции — множество . Тогда, очевидно, каждой точке функция f ставит в соответствие единственную точку . Отсюда следует, что все множество точек множества плоскости комплексная функция f отображает на множестве точек комплексной плоскости .

В этом состоит геометрический смысл комплексной функции комплексного переменного. Функцию будем называть отображением, множество называют образом множества при отображении до , а множество — прообразом множества при этом отображении.

Р ассмотрим некоторое подмножество множества и построим на плоскости множество точек

Множество называется образом множества при отображении , а множество — прообразом при этом отображении.

П ример 2.

Найти образ 1-го координатного угла комплексной плоскости при отображении .

Решение.

Найдем предварительно образ луча при отображении (рис. 2.2). Представим число z в показательней форме , тогда

, .

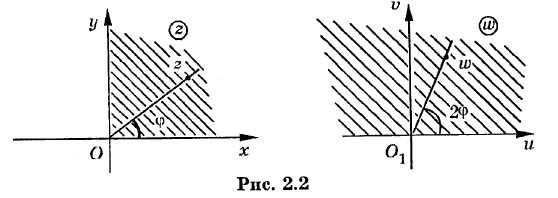
Е сли рассматривать z как любую точку луча плоскости ,то мы видим, что если луч Oz образует с осью Ох угол , то его образ-луч на плоскости образует с осью угол равный . Пусть теперь угол изменяется от нуля до , тогда луч Oz описывает ("заметает") первый координатный угол на плоскости , а его образ-луч опишет верхнюю полуплоскость плоскости , так как при изменении от до , изменяется от 0 до , где одно из значений аргумента z, a — одно из значений аргумента . Следовательно, образом первого координатного угла плоскости при отображении является верхняя полуплоскость плоскости .