24. Первообразная. Аналог формулы Ньютона-Лейбница для комплексных функций

Определение 5.7.

Аналитическая в области функция называется первообразной функции в , если для всех .

Если - первообразная функции в области , тогда, очевидно, функция - также первообразная функции при любом постоянном .

В самом деле

т.е. функция - первообразная функции .

Покажем, что других первообразных функция не имеет, т.е. любая первообразная имеет вид Пусть - любая первообразная функции отличная от . Тогда - функция аналитическая в области как разность двух аналитических функций.

Имеем далее

Выделим действительную и мнимую части функции

и тогда

(Смотри определение производной и систему Коши-Римана).

Из последнего равенства имеем в области

откуда вытекает в области , .т.е.

Значит, , что и требовалось доказать. Таким образом, совокупность всех первообразных функции в области выражается формулой , где - некоторая первообразная функции , и - комплексная постоянная.

Пусть - односвязная область и спрямляемая простая дуга, лежащая в . Интеграл по дуге от аналитической в функции по следствию из теоремы Коши для односвязной области не зависит от пути интегрирования.

Также, как упомянутое следствие, доказывается следующее утверждение.

Комплексный интеграл от непрерывной в односвязной области функции также не зависит от пути интегрирования, если интеграл от вдоль любой спрямляемой кривой, лежащей в , равен нулю. Для интеграла, не зависящего от пути интегрирования, естественно ограничиться указанием вместо пути интегрирования только его начала и конца , полагая

Теорема 5.2.

Пусть функция непрерывна в односвязной области и пусть интеграл от по любой спрямляемой замкнутой кривой, лежащей в , равен нулю. Тогда функция

есть первообразная функции в области .

Доказательство. Покажем, что в

Имеем

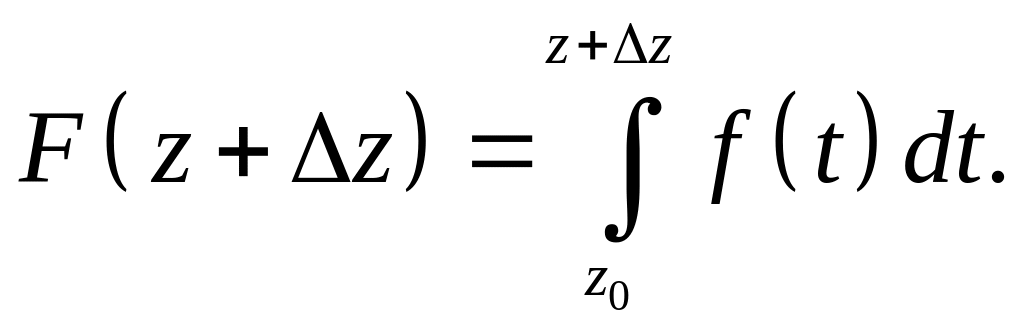
при этом будем предполагать, что интегрирование ведется по отрезку прямой, соединяющей точки и . Такое предположение можно ввести, так как по условию интеграл не зависит от пути интегрирования.

Для того, чтобы доказать, что

изучим модуль разности

.

В силу непрерывности функции в точке для любого , если . Поэтому при , а значит будем иметь

(Смотри свойство комплексного интеграла, содержащее в себе неравенство; в нашем случае длина кривой интегрирования - это длина отрезка соединяющего точки и . Эта длина равна ).

Итак, имеем при что равносильно

Теорема доказана.

Следствие.

Если функция аналитическая в односвязной области , то функция

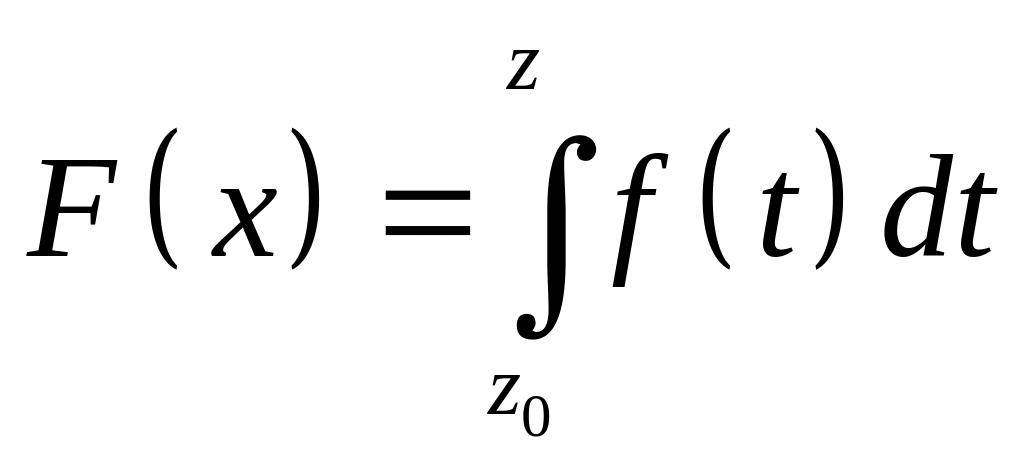
является первообразной для функции в области .

В самом деле, по теореме Коши для односвязной области для замкнутой кривой , тогда из теоремы вытекает утверждение следствия.

Теорема 5.3.

Если аналитична в односвязной области , то

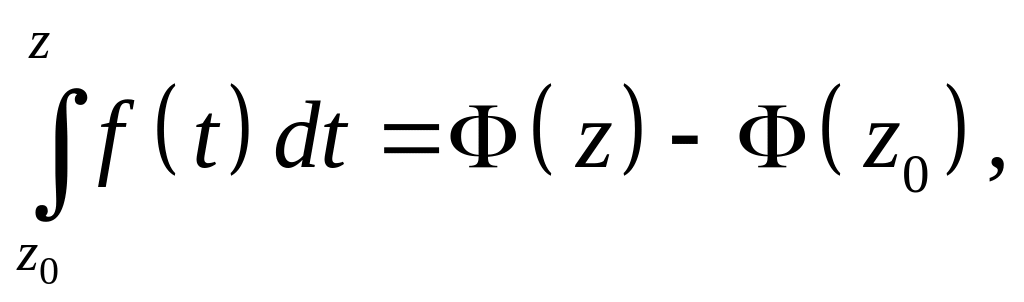
где - любая первообразная функции в области .

Доказательство.

Как нами показано, функция

является первообразной для функции , а любая другая первообразная имеет вид

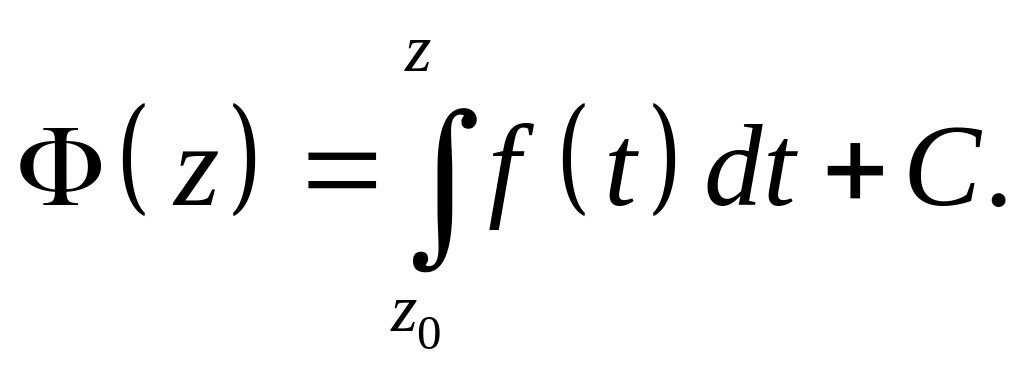
Полагая здесь имеем и тогда

что и требовалось доказать.

Замечание.

Пусть - многосвязная область и - аналитическая функция в . Если интеграл от по каждой спрямляемой замкнутой кривой, лежащей в , равен нулю, то к интегралу

можно применить все сказанное выше в этом пункте. Мы получим, что функции аналитична в , , , где - любая первообразная функции в . Если в многосвязной области существует хотя бы одна спрямляемая замкнутая кривая , для которой то для двух простых дуг, соединяющих c , значения интеграла от , вообще говоря, не будут равны и функция будет многозначной и говорить о ее производной не имеет смысла.