
- •1. Комплексные числа
- •2. Геометрическая интерпретация комплексных чисел и основных операций над ними
- •3. Тригонометрическая и показательная форма комплексного числа
- •4. Комплексной функции комплексного переменного
- •5. Действительная и мнимая части комплексной функции
- •6. Метризация комплексной плоскости. Последовательности комплексных чисел и их пределы
- •7. Предел комплексных функций
- •8.Непрерывность комплексных функций
- •9. Моногенность комплексных функций
- •10. Производная
- •11. Аналитические функции
- •12. Геометрический смысл модуля и аргумента производной
- •13. Конформные отображения
- •14. Линейная функция
- •15. Степенная функция с натуральным показателем
- •16. Показательная функция
- •17. Отображения, осуществляемые показательной функцией
- •18. Тригонометрические функции комплексного переменного
- •19. Гиперболические функции комплексного переменного
- •20. Логарифмическая функция комплексного переменного
- •21. Обратные тригонометрические функции
- •22. Интегрирование комплексных функций
- •Если интегрирование по замкнутой кривой проводится в направлении противоположном рассматриваемому ("по часовой стрелке") , то для обозначения интеграла употребляют символы.
- •23. Теорема Коши для односвязной области
- •24. Первообразная. Аналог формулы Ньютона-Лейбница для комплексных функций
- •25. Теорема Коши для многосвязной области
- •26. Формула Коши
- •27. Бесконечная дифференцируемость аналитической функции
- •28. Теорема Лиувилля. Основная теорема алгебры
- •30. Числовые комплексные ряды
- •31. Функциональные комплексные ряды
- •32. Степенные комплексные ряды
- •33. Разложение аналитической функции в степенной ряд Тейлора
Интегрирование проводится по замкнутой кривой в направлении (положительном), при котором конечная область , ограниченная кривой , остается слева. (Иногда такое направление интегрирования по кривой называют интегрированием по кривой "против часовой стрелки") (рис.5.4). Обозначают в этом случае интеграл одним из следующих символов
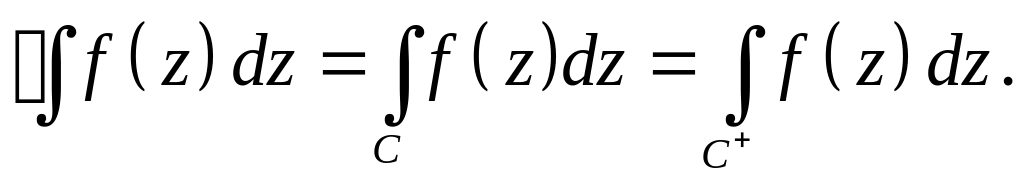
Если интегрирование по замкнутой кривой проводится в направлении противоположном рассматриваемому ("по часовой стрелке") , то для обозначения интеграла употребляют символы.
Последнее направление интегрирования называют также отрицательным.
Вычисление интеграла от комплексной функции.
Заменим в
интегральной сумме
![]()
получим:
![]()
![]()
Переходя в этом уравнении к пределу при
![]() одновременно, это означает, что все
одновременно, это означает, что все
![]() а
это в свою очередь означает, что
а
это в свою очередь означает, что
![]() и
и
![]() )
получим
)
получим
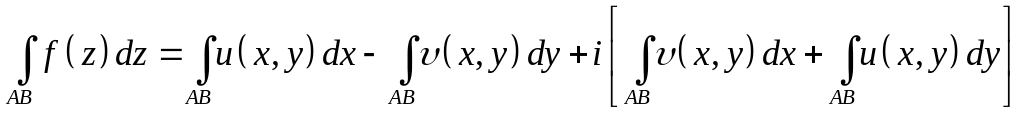
или в другой
записи
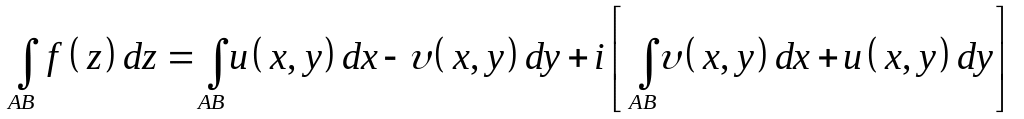
формула для вычисления интеграла от комплексной функции с помощью криволинейных интегралов от действительных функций двух действительных переменных.
Замечание 2.
Если кривая представляет замкнутую кривую и интегрирование проводится в положительном направлении, то последняя формула примет вид
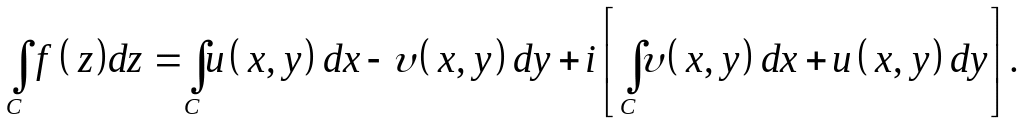
Замечание3.
Если
кривая
гладкая и задана в параметрическом виде
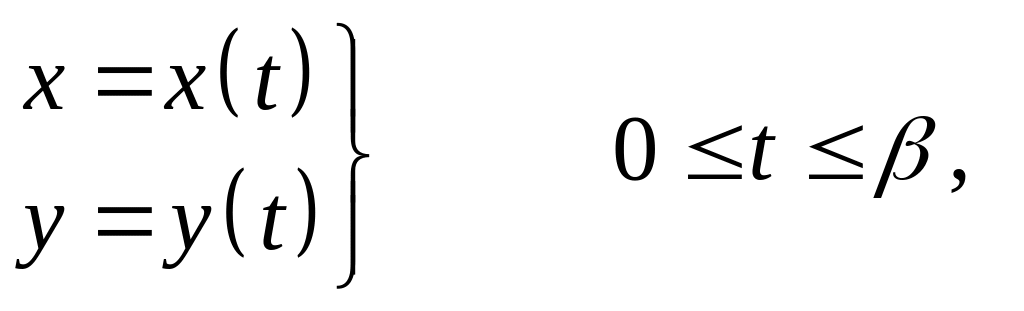
точка
имеет координаты
![]() точка
—
точка
—
![]() то
легко проверить, что из последних формул
получим
то
легко проверить, что из последних формул
получим
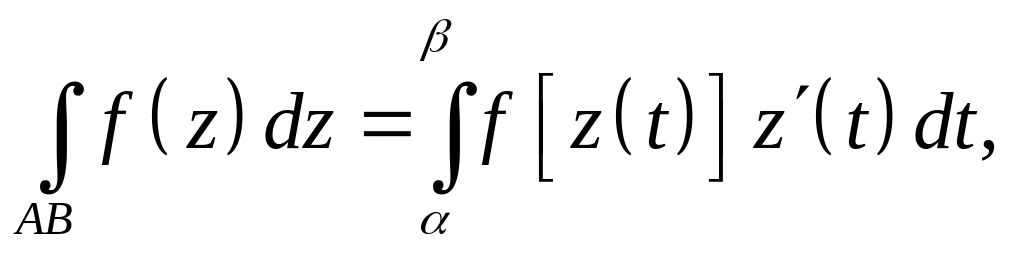
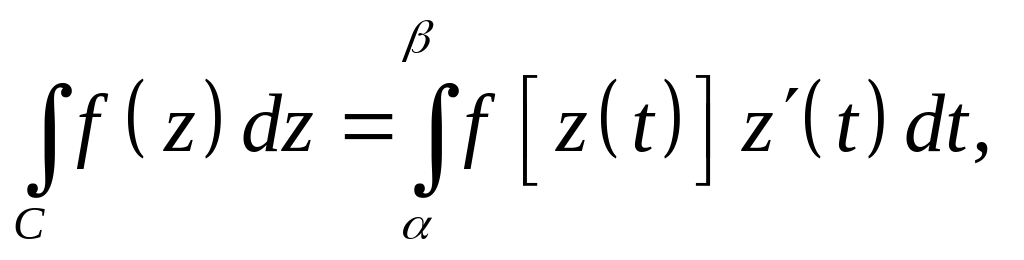
где
![]()
В случае
замкнутой кривой
![]() соответствует началу обхода этой кривой,
соответствует началу обхода этой кривой,
![]() - концу обхода).
- концу обхода).
Пример 3.
Вычислить интеграл
![]()
Из точки
проводим прямую
![]() параллельную оси
параллельную оси
![]() Тогда угол между лучом
и вектором
Тогда угол между лучом
и вектором
![]() является аргументом комплексного числа
является аргументом комплексного числа
![]()
![]() (рис.
5.5).
(рис.
5.5).
Теперь число
![]() можно представить в показательной
форме
можно представить в показательной
форме
![]()
При изменении
от
0 по
![]() точка
опишет окружность
.
Следовательно,
точка
опишет окружность
.
Следовательно,
![]() является комплексным уравнением
окружности
.
является комплексным уравнением
окружности
.
Для вычисления интеграла
используем формулу
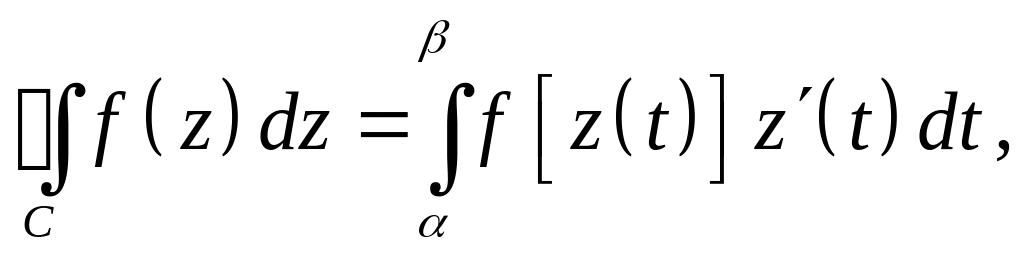
где уравнение
![]() является комплексным уравнением кривой
интегрирования
,
—
соответствует началу кривой интегрирования,
—
концу кривой интегрирования.
является комплексным уравнением кривой
интегрирования
,
—
соответствует началу кривой интегрирования,
—
концу кривой интегрирования.
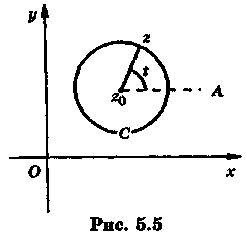
В случае нашего примера
![]()
![]()
![]()
Итак,
![]()
Свойства комплексного интеграла:
1.
![]()
Доказательство:
![]()
Интегральная
сумма
![]()
в этом случае имеет вид:
![]()
![]()
Следующие
свойства 2-6 вытекают из формулы
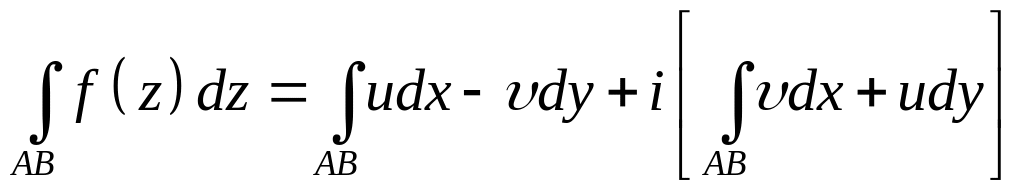
и соответствующих свойств интегралов от действительных функций двух действительных переменных
2.
![]()
3.
4.
![]()
5.
![]()
если
![]() (рис. 5.6).
(рис. 5.6).
6. Если комплексная функция непрерывна на кривой , то она интегрируемы по этой кривой.
7. Если на
кривой
имеем
![]() то
то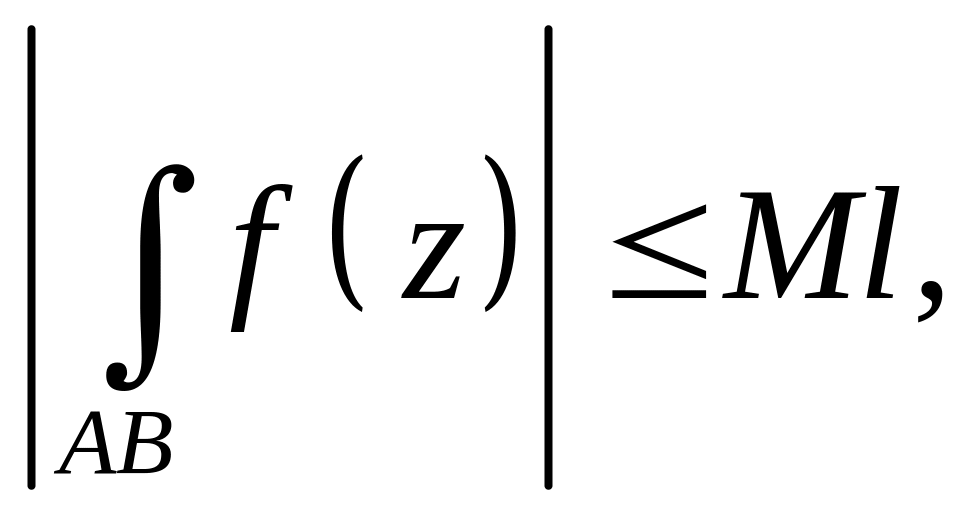
где — длина кривой интегрирования .
Доказательство.
![]() (рис. 5.7).
(рис. 5.7).
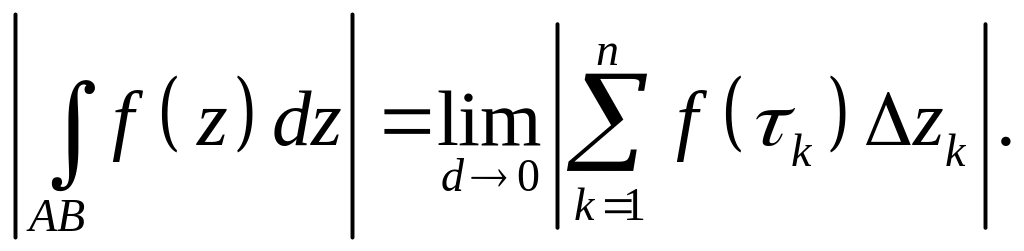 Но
Но
![]()
![]() —
длина
-
го звена ломаной
—
длина
-
го звена ломаной
![]() вписанной в кривую
,
вписанной в кривую
,
![]() —
длина ломаной
—
длина ломаной
![]() которая
меньше длины
кривой
,
т.е.
которая
меньше длины
кривой
,
т.е.
![]() и, следовательно
и, следовательно
![]()
Переходя
в этом неравенстве к пределу и учитывая,
что
![]() получим доказываемое утверждение.
получим доказываемое утверждение.
23. Теорема Коши для односвязной области
Для формулировки и доказательства теоремы Коши приведем некоторые определения.
Определение 5.5.
Область
![]() называется
односвязной, если внутренность любой
замкнутой кривой
,
принадлежащей области
, состоит только из точек данной области.
называется
односвязной, если внутренность любой
замкнутой кривой
,
принадлежащей области
, состоит только из точек данной области.
Определение 5.6.
Комплексная функция
называется аналитической в области
и на ее границе
,
если эта функция аналитична в некоторой
области
![]() ,
содержащей область
вместе с ее границей
.
,
содержащей область
вместе с ее границей
.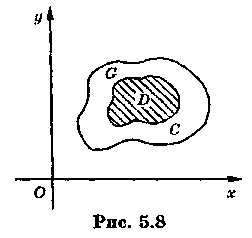
Теорема 5.1.
Если
функция
аналитична в односвязной области
,
то интеграл по любой спрямляемой
замкнутой кривой
,
принадлежащей области
,
равен нулю, т.е.
![]() (рис. 5.8).
(рис. 5.8).
Доказательство .
Доказательство теоремы приведем для
случая, когда кривая
пересекается прямыми параллельными
координатным осям не более чем в двух
точках, точках,
а частные производные
![]() функции
функции
![]() непрерывны в области
.
непрерывны в области
.
Для доказательства теоремы нам потребуется формула Грина:
![]()
где - область, ограниченная кривой .
Применим формулу Грина к действительной
и мнимой частям правой части формулы
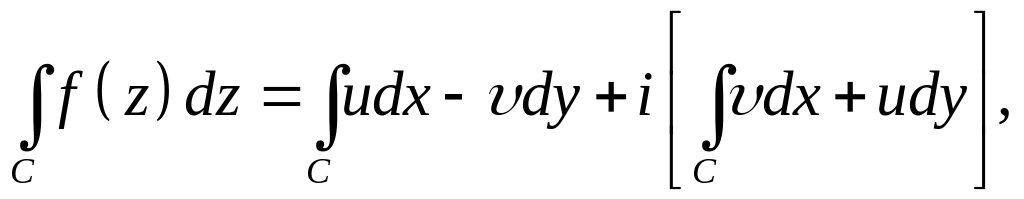
учитывая, что для аналитической функции
в области
выполняются условия Коши-Римана
![]()
Имеем по формуле Грина
![]()
так как в области
в силу условий Коши-Римана
![]()
Аналогично докажем, что
![]()
а, значит
![]()
Что и требовалось доказать.
Следствие 1.
Если комплексная функция
аналитична в односвязной области
и на ее границе
,
то
![]()
В самом деле, если функция аналитична в области и на ее границе , то это означает, что существует область , содержащая область вместе с границей , и при этом в области функция аналитична, а тогда по теореме 5.1. имеем утверждение следствия 1.
Следствие 2.
Если функция
аналитична в односвязной области
,
то интеграл от этой функции не зависит
от пути интегрирования, т.е., если
![]() и
и
![]() - любые две точки области
, a
- любые две точки области
, a
![]() и
и
![]() -
две любые спрямляемые кривые,
соединяющие эти точки (рис. 5.9), то
-
две любые спрямляемые кривые,
соединяющие эти точки (рис. 5.9), то
![]()

В самом деле по теореме Коши имеем
![]()
Используя свойства интегралов, имеем
![]()
т.е.
![]()
что и требовалось доказать.
