
- •1. Комплексные числа
- •2. Геометрическая интерпретация комплексных чисел и основных операций над ними
- •3. Тригонометрическая и показательная форма комплексного числа
- •4. Комплексной функции комплексного переменного
- •5. Действительная и мнимая части комплексной функции
- •6. Метризация комплексной плоскости. Последовательности комплексных чисел и их пределы
- •7. Предел комплексных функций
- •8.Непрерывность комплексных функций
- •9. Моногенность комплексных функций
- •10. Производная
- •11. Аналитические функции
- •12. Геометрический смысл модуля и аргумента производной
- •13. Конформные отображения
- •14. Линейная функция
- •15. Степенная функция с натуральным показателем
- •16. Показательная функция
- •17. Отображения, осуществляемые показательной функцией
- •18. Тригонометрические функции комплексного переменного
- •19. Гиперболические функции комплексного переменного
- •20. Логарифмическая функция комплексного переменного
- •21. Обратные тригонометрические функции
- •22. Интегрирование комплексных функций
- •Если интегрирование по замкнутой кривой проводится в направлении противоположном рассматриваемому ("по часовой стрелке") , то для обозначения интеграла употребляют символы.
- •23. Теорема Коши для односвязной области
- •24. Первообразная. Аналог формулы Ньютона-Лейбница для комплексных функций
- •25. Теорема Коши для многосвязной области
- •26. Формула Коши
- •27. Бесконечная дифференцируемость аналитической функции
- •28. Теорема Лиувилля. Основная теорема алгебры
- •30. Числовые комплексные ряды
- •31. Функциональные комплексные ряды
- •32. Степенные комплексные ряды
- •33. Разложение аналитической функции в степенной ряд Тейлора
16. Показательная функция
Как
известно, при
действительном имеем
![]() .
.
Аналогично
определяем
![]() ,
если
– комплексное.
,
если
– комплексное.
Можно
показать [5], что
![]() ,
,
![]() .
.
(Здесь
и ниже символ
![]() означает одно из значений аргумента
означает одно из значений аргумента
![]() ).
).
Таким образом, комплексная показательная функция с комплексным показателем определяется равенством
![]() , (4.7)
, (4.7)
так как
![]() .
.
Свойства показательной функции.
1. Область
определения показательной функции –
все множество
комплексных чисел, т.е.
![]() .
Утверждение следует из
того, что действительная функция
.
Утверждение следует из
того, что действительная функция
![]() определена при любом
действительном
,
а действительные функции
определена при любом
действительном
,
а действительные функции
![]() и
и
![]() определены
при любом действительном
,
а поэтому формула (4.7) имеет
смысл при любом комплексном
.
определены
при любом действительном
,
а поэтому формула (4.7) имеет
смысл при любом комплексном
.
2. ![]() ;
;
![]() .
.
Это свойство следует из формулы (4.7).
3. Показательная функция принимает любое комплексное значение, кроме нуля, т.е. множество значений (область значений) показательной функции
![]() .
.
Показательная функция не принимает нулевого значения, так как
![]() .
.
Покажем теперь, что показательная функция примет значение любого комплексного числа , т.е. покажем, что уравнение
(4.8)
разрешимо относительно при любом .
Представим в тригонометрической форме:
![]() , (4.9)
, (4.9)
где
– одно из значений
,
например, пусть
![]() – главное
значение
.
– главное
значение
.
Теперь на основании (4.7) и (4.9) уравнение (4.8) примет вид:
![]() .
.
Отсюда
![]() ,
,
![]() ,
;
,
;
Итак,
мы нашли решение уравнения (4.8)
![]() ,
(4.10)
при
любом
.
,
(4.10)
при
любом
.
Свойство доказано.
4. ![]() .
.
Пусть , .
Тогда
![]() . (4.11)
. (4.11)
(Последнее равенство получено на основании формулы (4.7)) С другой стороны
![]()
![]()
![]() . (4.12)
. (4.12)
Из (4.11) и (4.12) имеем доказываемое утверждение
5.
Показательная
функция аналитична во всей комплексной
плоскости и
![]() .
.
Из
определения показательной функции
имеем
![]() .
.
Следовательно,
![]()
![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Частные
производные непрерывны в каждой точке
![]() ,
так
как для любых
и
непрерывны функции
,
так
как для любых
и
непрерывны функции
![]() ,
,
![]() ,
,
![]() .
Легко
заметить также, что в любой точке
комплексной плоскости выполняются
условия Коши-Римана:
;
.
.
Легко
заметить также, что в любой точке
комплексной плоскости выполняются
условия Коши-Римана:
;
.
Выполнение
этих условий и непрерывность частных
производных
,
,
,
во
всей комплексной плоскости означает
аналитичность показательной функции
во всей комплексной
плоскости. Для нахождения производной
показательной функции
воспользуемся формулой
![]()
![]() ;
;
![]() .
.
6. Показательная функция непрерывна во всей комплексной плоскости. Непрерывность функции следует из её аналитичности. (Функция аналитическая во всей комплексной плоскости дифференцируема в каждой точке плоскости, а из дифференцируемости всегда следует непрерывность функции).
7.
Показательная
функция периодична с периодом равным
![]() .
.
В
самом деле
![]()
![]() .
.
Замечание. Любой другой период показательной функции имеет вид
![]() ,
,
,
,
т.е.,
если
![]() , (4.13)
то
, (4.13)
то
![]() ,
,
![]() ,
.
,
.
Пусть
имеем (4.13), тогда
![]() .
Положим
.
Положим
![]() ,
тогда
,
тогда
![]() .
.
![]() ,
,
![]() ,
,
. (4.14)
,
,
. (4.14)
Из
(4.14) следует, что
![]() ,
тогда
,
тогда
![]() ,
,
.
,
,
.
Что и требовалось доказать.
8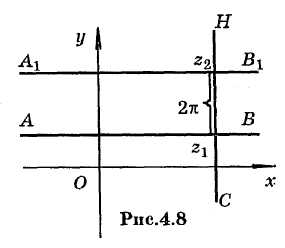 .
Показательная
функция однолистна
во всякой открытой горизонтальной
полосе ширины не больше
.
.
Показательная
функция однолистна
во всякой открытой горизонтальной
полосе ширины не больше
.
Утверждение
будет доказано, если
мы покажем, что нарушение однолистности
возможно лишь на границах
указанной полосы, т.е.
![]() при
при
тогда
и только тогда, когда
![]() ,
например, при
и
лежат
па пересечении перпендикуляра
,
например, при
и
лежат
па пересечении перпендикуляра
![]() с прямыми
с прямыми
![]() и
и
![]() ,
расстояние между которыми
равно
(рис.4.8).
,
расстояние между которыми
равно
(рис.4.8).
Итак,
пусть
и
.
Тогда
![]() ,
где
,
где
![]() .
.
Но
![]() ,
как показано в предыдущем свойстве,
всегда равно
,
т.е.
,
как показано в предыдущем свойстве,
всегда равно
,
т.е.
![]() .
Итак,
.
Итак,
![]() ,
,
если
,
что и требовалось доказать.
,
,
если
,
что и требовалось доказать.
