2. Решение 2 2-игр

Рассмотрим матричную игру, в которой каждый из игроков имеет по две чистые стратегии. В общем виде 2 2-игра определяется матрицей

H = .

Пусть Х – произвольная смешанная стратегия игрока Ι. Если х – вероятность выбора игрока Ι своей первой чистой стратегии в условиях Х, то вероятность выбора им второй чистой стратегии есть 1 – х. Поэтому стратегию Х можно представить в виде (х, 1 – х). Аналогично если Y – произвольная смешанная стратегия игрока ΙΙ, то она имеет вид (y, 1 – y). Таким образом, стратегия Х однозначно определяется числом х, а стратегия Y – числом y. В соответствии с этим мы будем обозначать ситуацию (X, Y) как пару чисел (х, y). В силу предположения, что чистых оптимальных стратегий нет, х^* > 0 и y^* > 0.

На основании теоремы 7:

(20)

и

(21)

Если v ≠ 0 и игроки имеют только смешанные оптимальные стратегии, определитель матрицы Н отличен от нуля. Из этого следует, что системы уравнений (20) и (21) имеют единственное решение. Решая их, находим

х^* = , у^* = ,

v = . (22)

Таким образом, для решения матричной 2 2-игры необходимо сначала проверить равенство (8). Если оно выполняется, то игроки имеют чистые оптимальные стратегии (игрок Ι – чистую максиминную, а игрок ΙΙ – чистую минимаксную). В противном случае по формулам (22) следует найти оптимальные стратегии игроков и значение игры.

П р и м е р 7

Решить игру Н = .

Решение. Прежде всего проверим наличие седловой точки (в чистых стратегиях). Имеем

max min h_ij = 1, min max h_ij = 2,

^{i {1, 2} j {1, 2} j {1, 2} i {1, 2}}

и следовательно, седловых точек нет. Перейдем к нахождению оптимальных смешанных стратегий и значения игры. Используя формулы (22), получим:

х^* = = , у^* = = , v = = .

Таким образом, Х^* = Y^* = v =

П р и м е р 8

Решить игру из примера 6.

Решение. Используя доминирование, мы свели эту игру к эквивалентной игре с матрицей выигрышей

Н' = .

Так как max min h' = 4, а min max h_ij = 6,

^{i {1, 2} j {1, 2} j {1, 2} i {1, 2}}

Седловых точек в чистых стратегиях нет. Перейдем к нахождению решения в смешанных стратегиях. По формулам (22) имеем

х = у = v =

и, следовательно, Х^* = ( ,0, 0, ), Y^* = (0, , 0, 0), v = .

3. Графический метод решения игр

2 n и m 2

Предварительно докажем одно утверждение.

Теорема 8. В равенстве (8) внутренние экстремумы достигаются на чистых стратегиях, т. е.

max min H (X, Y) = max min H (X, j) = max min XH ._j ,

^{Х S Y S Х S j B Х S j B}

min max H (X, Y) = min max H (i, Y) = min max H_i.Y^T.

^{Y S Х S Y S i A Y S i A}

1. Рассмотрим игру, в которой игрок Ι имеет две чистые стратегии, а игрок ΙΙ – произвольное число n число стратегий. Матрица выигрышей этой игры имеет вид

H = _. (26)

Произвольная смешанная стратегия игрока Ι имеет вид Х = (х, 1 – х), а их множество можно описать сегментом [0, 1]. Из теоремы 8 следует, что целью игрока Ι является максимизация величины

h (x) = min [h_1jx + h_2j (1 – x) ]. (27)

Графическая зависимость выигрыша

H (X, j) = XH._j = h_1jx + h_2j (1 – x)

от х изображается прямой линией. Каждой чистотой стратегии j игрока ΙΙ соответствует своя прямая (рис. 2, 3).

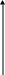
H h_1j' H

h_2j''

v ^м h_1j'' v j'

h_2j'

0 x^* 1 x 0 {x^*} 1

Рис. 2 Рис. 3

Ясно, что матрица (26) имеет одинаковые столбцы, то прямые, соответствующие таким стратегиями игрока ΙΙ, будут совпадать. Все совпадающие столбцы будем считать за одну стратегию. Графиком функции (27) является нижняя огибающая всех прямых, соответствующих стратегиям игрока ΙΙ (на рис. 2 она выделена жирной линией). Максимуму функции h (х) соответствует наивысшая точка М огибающей, т. е.

max h (x) = max min [h_ijx + h_2j (1 – x) ].

^{X [0, 1] X [0, 1] j B}

Так как

max min [h_ijx + h_2j (1 – x) ] = max min Н (х, j) =

^{X [0, 1] j B X [0, 1] j B}

= max min H (X, Y),

^{X [0, 1] Y S}

по основной теореме (теорема 5)

v = max h (x)

^{X [0, 1]}

и, следовательно, абсцисса точки М является оптимальной смешанной стратегией игрока Ι, а её ордината – значением игры. Если таких точек более одной, то огибающая будет иметь наивысший горизонтальный участок и у игрока Ι существует бесконечное множество оптимальных смешанных стратегий, состоящее из всех абсцисс этих точек (см. рис. 3).

Пусть точка М – точка пересечения прямых h_j' (х) и h_j'' (х). Тогда значение игры v и стратегию х^* = (х^*, 1 – х^*) мы найдем, решая следующую систему:

Эти величины, однако, могут быть вычислены и с помощью формул (22) для игры

Н' = . (28)

Для полного решения задачи нам необходимо найти и оптимальную стратегию Y^* = (y , y , …, y ) игрока ΙΙ с помощью описанного построения. При этом могут представиться две возможности.

Во-первых, огибающая имеет верхний горизонтальный участок (см. рис. 3), соответствующий чистой стратегии j⁰ игрока ΙΙ. Очевидно, это может быть лишь при h = h . В таком случае игрок ΙΙ имеет единственную оптимальную стратегию, которая является чистой, т. е.

Y^* = (0, …, 0, 1, 0, …, 0).

^j

Во-вторых, может оказаться, что график функции (27) имеет единственную верхнюю точку М.

Если абсцисса «пиковой» точки является 0 или 1, то игрок Ι имеет чистую оптимальную стратегию (в случае, изображенном на рис. 4, это точка 0) и существует прямые

h_1jx + h_2j (1 – x) = H, (29)

подходящие к точке М, не убывая при приближении к ней. Эти прямые, очевидно, соответствуют чистым оптимальным стратегиям игрока ΙΙ. Все «смеси» этих стратегий также оптимальны. Кроме того, могут иметься еще прямые (29), подходящие к точке М убывая. Они не соответствуют оптимальным стратегиям игрока ΙΙ. Однако те их «смеси» со строго убывающими прямыми, которые не убывают, также являются оптимальными стратегиями игрока ΙΙ. В заключение следует перейти к выпуклой оболочка всех полученных стратегий.

Если абсцисса точки М лежит

с трого между 0 и 1 (см. рис. 2), Н

т о существует хотя бы одна про- _м

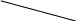
х одящая через М прямая (29), v

имеющая положительный наклон,

и хотя бы одна прямая, имеющая

о трицательный наклон. 0 1 x

Рис. 4

Пусть

h_1j'x + h_2j' (1 – x) = Н,

h_1j''x + h_2j'' (1 – x) = Н (30)

эти прямые (соответствующие стратегии имеют номера j', j''). Решение уравнений (30) дает нам

x_M = и v = Н_М =

Из того, что прямые (30) пересекаются в точке М с ординатой v и имеют наклоны разных знаков, следует существование такого

y_j' (0, 1), что «смесь» этих прямых с весами y_j' и y_j'' = 1 - y_j' является горизонтальной прямой, проходящей через данную точку. Так как ординаты точек пересечения горизонтальной прямой с прямыми х = 0 и х = 1 будут равными (в частности, равными v), справедливо равенство

(h_1j' – h_1j'') y_j' + h_1j'' = (h_2j' – h_2j'') y_j' + h_2j''.

Решая это уравнение, получим

y_j' = · (31)

Смешанная стратегия игрока ΙΙ, состоящая из его стратегий Н._j' и Н._j'', взятая с найденными весами y_j' и y_j'' = 1 - y_j' (Y^* = (0, …, 0, y_j', 0, …, 0, y_j'', 0, …, 0)), будет давать игроку Ι ровно v независимо от того, как он сам будет играть. Следовательно, эта смешанная стратегия игрока ΙΙ является его оптимальной стратегией. Значение y_j' можно найти, используя также формулы (22) для игры с матрицей (28). Комбинируя таким образом каждую прямую стратегию с положительным наклоном и каждую прямую стратегию с отрицательным наклоном, мы получили некоторое множество Y ,Y , …, Y оптимальных стратегий игрока ΙΙ. Затем следует перейти к их выпуклой оболочке

{Y^*} = λ₁ Y + … + λ_kY , λ₁, …, λ_k ≥ 0, λ_i = 1.

П р и м е р 9

Решить игру Н =

Решение. Построим прямые

(1): Н = 2 · х + 4 · (1 – х) = -2х + 4;

(2): Н = 3 · х + 1 · (1 - х) = 2х + 1;

(3): Н = 1 · х + 6 · (1 – х) = -5х + 6;

(4): Н = 5 · х + 0 · (1 – х) = 5х.

Построим нижнюю огибающую прямых (1) – (4) (рис. 5). Она имеет «пиковую» точку М, которая лежит строго между 0 и 1. Абсциссу точки М (точки пересечения прямых (2) и (3)) найдем, решая уравнение

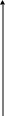
Н

2х^* + 1 = -5х^* + 6.

(4)

С ледовательно, х^* = 5/7 и v = Н_М =

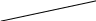= 17/7. (2)

Применяя формулы (22) для игры ^j' м (1)

1 (3)

Н' = , 0 х^* 1 х

Рис. 5

найдем оптимальную стратегию игрока ΙΙ:

у^* = = .

Таким образом,

Х^* = , Y^* = , v = .

П р и м е р 10

Решить игру Н = ·

Решение. Построим прямые

(1): Н = 1 · х + 1 · (1 – х) = 1;

(2): Н = 2 · х + 0 · (1 – х) = 2х;

(3): Н = 0 · х + 2 · (1 – х) = -2х + 2.

Построим нижнюю огибающую прямых (1) – (3) (рис. 6).

Она имеет «пиковую» точку М, Н

которая лежит строго между 0 и

1. Решая уравнение

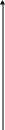
2х^* = -2х^* + 2, (2)

найдем х^* = ½ и, следовательно, v м ^j

v = Н_М = 1. 1 (1)

Применяя формулы (22) для ^{j' j''} (3)

и гры

0 х^* 1 х

Н' = , Рис. 6

найдем оптимальную стратегию игрока ΙΙ:

у^* = = , и Y =

Так как через точку М проходит горизонтальная прямая (1), Y = (1, 0, 0).

Таким образом,

Х^* = ( ), {Y^*} = λ₁Y + λ₂ Y (λ₁, λ₂ ≥ 0, λ₁ + λ₂ = 1), v = 1.

2. Пусть теперь в матричной игре две чистые стратегии имеет игрок ΙΙ, а игрок Ι – их произвольное число m. Это означает, что матрица выигрышей такой игры имеет следующий вид:

H = . (32)

Анализ игры подобного вида сходен с приведенным выше анализом 2 n-игр. Произвольная смешанная стратегия игрока ΙΙ имеет вид Y = (у, 1 – у), а их множество можно описать сегментом [0, 1]. Из теоремы 8 следует, что целью игрока ΙΙ является минимизация величины

h (y) = max [h_i1y + h_i2 (1 – y)]. (33)

^{i А}

Графически зависимость выигрыша

H (i, Y) = H_i.Y^T = h_i1y + h_i2 (1 – y)

от у изображается прямой линией. Каждой чистой стратегии игрока Ι соответствует своя прямая (рис. 7).

Графиком функции (33) будет верхняя огибающая всех прямых, соответствующих стратегиям игрока Ι (на рис. 7 она выделена жирной линией). Минимуму функции h (y) соответствует нижняя точка М огибающей, т. е.

min h (y) = min max [h_i1y + h_i2 (1 – y)].

^{y [0, 1] y [0, 1] i А}

Так как

min max H (i, y) = min max H (X, Y),

^{y [0, 1] i А y [0, 1] X S}

п о основной теореме (теорема 5) Н

h_i' 2 ^i'

v = min h (y) v M h_1'' 1

^{y [0, 1]} h_i'' 2 ^i''

и, следовательно, абсцисса точки М

является оптимальной смешанной h_1' 1

с тратегией игрока ΙΙ, а её ордината –

значением игры. 0 y* 1 y

Рис. 7

П р и м е р 11

Решить игру Н = .

Решение. Построим прямые

(1): Н = 4 · у + 3 · (1 – у) = у + 3;

(2): Н = 2 · у + 4 · (1 – у) = -2у + 4;

(3): Н = 0 · у + 5 · (1 – у) = -5у + 5;

(4): Н = -1 · у + 6 · (1 – у) = -7у + 6.

Построим верхнюю огибающую прямых (1) – (4) (рис. 8). Её нижняя точка М лежит строго между 0 и 1.

Н Далее,

(1) у^* + 3 = -7у^* + 6, у^* =

М

v

(2) v = H_M =

(3)

0 у^* 1 у Применяя формулы (22) для иг-

(4) ры

Рис. 8 Н' = .

найдем оптимальную стратегию иг-

рока Ι

х^* = = .

Таким образом,

Х^* = , 0 , 0, , Y^* = , , v = .

Замечание 4. Графический способ, подобный описанному, можно применить и к решении игр 3 n и m 3. Однако получающиеся при этом построения оказываются весьма громоздкими и требуют привлечения методов начертательной геометрии. При m > 3 (n > 3) графическое решение игры практически невозможно.