Мнемоническое правило вычисления z-передаточной функции многоконтурной системы со вложенными контурами.

_|_

_|_

_|_

_|_

_{_|_}

_|_

Для такой системы можно сразу записать z-передаточную функцию, если она существует, можно определить в виде дроби:

z- передаточная функция i-го контура в разомкнутом состоянии, берется со знаком “+”, или контур содержит ООС, и “-”, или ПОС.

_{_|_}

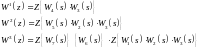
- если бы не было , было бы преобразование от

_|_

_|_

_|_

_|_

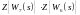
Частотные методы исследования дискретных систем.

Рассмотрим упрощенные модели.

Преобразование спектра сигналов импульсным модулятором.

_|_

=

Рассмотрим преобразование Лапласа этого сигнала

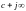
Рассмотрим преобразование спектра сигнала

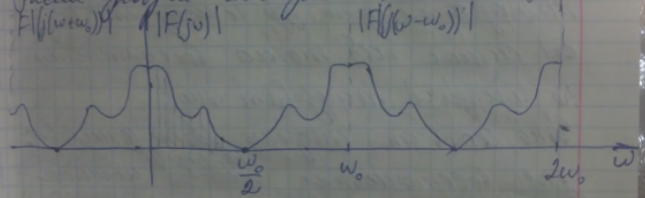
В результате импульсной модуляции из исходного спектра возникли смещенные по частоте составляющие более высоких частот. Их еще называют транспонированные составляющие, т.е. транспонирование из НЧ области в ВЧ область. По существу это помехи, которые …. импульсной модуляцией.

В данном случае при 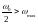, дополнительные составляющие (транспонированные) не накладываются друг на друга и исходный входной сигнал может быть точно восстановлен по импульсной последовательности.

Это соответствует теореме Котельникова. Для восстановления непрерывного сигнала по импульсной последовательности необходимо и достаточно что бы частота повторения , по крайней мере в 2 раза превышала такую частоту пр –ю в спектре.

Рассмотрим случай

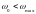
В данном случае ….. 2…..транспонирования частот.

1. Транспонирование НЧ сигнала в ВЧ область

2. Транспонирование ВЧ сигнала в НЧ область

В данном случае, , не удается восстановить исходный непрерывный сигнал…….транспонирования в НЧ область и смешивания исходных и импульсных спектров.

Неприятно транспонирование ВЧ->НЧ, т.к. НЧ обычно обрабатывается СУ и …….. и мешают работе системы.

Частотные характеристики импульсной системы.

_|_

_|_

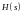
Преобразование Лапласа импульсного сигнала:

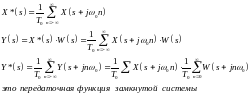
Таким образом, передаточная функция представлена в виде бесконечной суммы смещенных на передаточных функций исходного непрерывного звена.

Свойства частотных характеристик дискретных систем.

1. Частотная характеристика дискретной системы имеет формальный характер и мало отражает смысл преобразования гармонического сигнала.

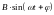
Д

ля дискретной системы:

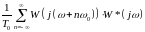
2. Частотная характеристика дискретной системы есть переходная функция частоты с периодом

Т.е. разные гармонические сигналы передаются одинаково в дискретной системе.

t

3. Частотная характеристика дискретной системы представляется в виде | | и аргумента.

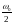
Н

адо знать только АЧХ от 0 до , остальное повторяется.

Таким образом, частотные характеристики определяются расположением частот размером в

Лекция