
- •Квантование по уровню и квантование по времени
- •Импульсные системы. Вид импульсной модуляции.
- •Математическая модель импульсного элемента.
- •Обобщенная схема импульсной системы.
- •Преобразование Лапласа импульсного сигнала. Z-преобразование.
- •Основные свойства z-преобразования:
- •Вычисление преобразования Лапласа импульсного сигнала по известному преобразованию Лапласа непрерывного сигнала.
- •Решетчатые функции и их разности. Смещенная решетчатая функция.
- •Конечная разность решетчатой функции.
- •Понятия о разностных уравнениях.
- •Порядок разностных уравнений и оператор сдвига
- •Решение разностных уравнений. Рекуррентный способ решения.
- •Физический смысл однородного и неоднородного разностного уравнения
- •Корневые условия устойчивости:
- •Вычисление z-передаточной функции.
- •Свойства z-передаточной функции.
- •Модифицированное z-преобразование и модифицированные z-передаточные функции.
- •Алгебра z-перед функций и структурных преобразований.
- •Мнемоническое правило вычисления z-передаточной функции многоконтурной системы со вложенными контурами.
- •Частотные методы исследования дискретных систем.
- •Преобразование спектра сигналов импульсным модулятором.
- •Частотные характеристики импульсной системы.
- •Свойства частотных характеристик дискретных систем.
- •Логарифмические частотные характеристики.
- •Псевдочастота (пч) и псевдочастотные характеристики (пчх)
- •Методы построения частотных характеристик.
- •Прохождение гармонического сигнала через дискретную цепь
Корневые условия устойчивости:
Если все корни характеристического уравнения по модулю будут меньше 1
 ,
то такая система устойчива (притом
асимптотически)
,
то такая система устойчива (притом
асимптотически)Если среди корней характеристического уравнения есть корень
 или
или
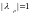 - кратный, то неустойчива, расходящееся
движение.
- кратный, то неустойчива, расходящееся
движение.Если есть корни
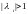 и есть кроме них корни
и есть кроме них корни
 - простые, то система устойчива по
Ляпунову, не асимптотически (не
разбегается).
- простые, то система устойчива по
Ляпунову, не асимптотически (не
разбегается).
Устойчивость асимптотическая (все корни<1). (Решение – точки)
x[k]

k
неустойчивая:


Система устойчива, но не асимптотически (на границе устойчивости)


Пример:
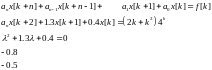
Система асимптотически устойчива, т.к. корни мо модулю меньше 1
Лекция 5

W(s)
_|_
_|_
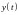
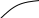

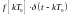
То 2То 3То t

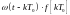


kТо t
Общая реакция непрерывного звена будет определятся суммой на каждый отдельный -импульс.
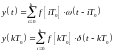
Импульсный сигнал:

Подставляем:

При аргументе =0, весовая функция =0

Введем переменные:

Введем преобразование Лапласа от импульсного сигнала
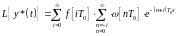
 т.к. весовая функция для
физически реализуемой системы = 0.
т.к. весовая функция для
физически реализуемой системы = 0.



 - дискретная передаточная
функция звена
- дискретная передаточная
функция звена
 z – преобразование
z – преобразование
z – изображение входа = z
– изображение входного сигнала * z
– передаточную функцию
– изображение входа = z
– изображение входного сигнала * z
– передаточную функцию

z – передаточная функция – это z – преобразование весовой решетчатой функции звена.

W(z)
F(z) Y(z)
Вычисление z-передаточной функции.

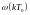

Nэф*Е0
Nэф – время, за которое функция практически заканчивается
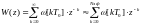
 - время, за которое весовая
функция практически заканчивается
- время, за которое весовая
функция практически заканчивается
2.
способ



Свойства z-передаточной функции.
Передаточная функция есть дробно-рациональная от z, многочлен в числителе и многочлен в знаменателе.


Передаточная функция есть дробно-рациональная функция от z
Функция - периодическая функция по S, с …….. периодом, т.е.

Дискретная передаточная
функция
 является периодической функцией с
мнимым периодом
является периодической функцией с
мнимым периодом
 - частота квантования, то
- частота квантования, то

3.
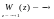 действительному числу,
если нет полюсов zi =1
действительному числу,
если нет полюсов zi =1
Определяет статический коэффициент передачи (предел при z0)
Порядок многочлена знаменателя z-перед функции равен порядку многочлена знаменателя s-передаточной функции, поскольку каждый полюс
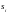 переходит в полюс
переходит в полюс


При изменении нулей передаточной функции изменяется только числитель дискретной передаточной функции, а при изменении полюсов s-передаточной функции изменяется все.

