15. Вакансионные комплексы.

При случайной встрече одиночные вакансии мигрируют, объединяются в пары – дивакансии. При этом уравновешивается их суммарная поверхность и соответствующий выигрыш в поверхностной энергии, обеспечивает усталостность спаренной вакансии. Энергию образования дивакансии можно оценить следующим путем. Если удалить атом являющейся в плотной упаковки соседом вакансии, то образуется дивакансия. В этом случае число разрыва связей в расчете на одну вакансию будет на единицу меньше, чем при образование двух одиночных вакансий. Разность между суммарной энергией образования двух изолированных вакансий и энергией образования дивакансии, называется энергией связи дивакансии , .Тогда энергия образования дивакансии будет равна . Если в решетке имеется N узлов и координатное число Z, то в решетке имеется ZN/2 пар соседних узлов. Тогда можно разместить n₂ дивакансий по парам соседних узлов следующим

образом . Конфигурационная энтропия при появление n₂ дивакансий возрастает на величину (6)

если пренебречь колебательной энтропией, то изменение свободной энергии, при появление n₂ дивакансий в кристалле будет составлять

(7)

Используя формулу Стирлинга и приравнивая первую производную от по n₂ к 0 получим выражение для равной концентрации диваканций

(8)

Это выражение можно представить по другому

(9) (9.1)

Тогда (9) с учетом выражения (9.1) получаем, что равновесная концентрация дивакансий связана (10)

Отсюда видно, что равновесная концентрация дивакансий растёт с повышением температуры. Из формулы (9,1) и (8) можно получить выражение

(11)

С повышением температуры отношение равновесных дивакансий к моновакансиям растёт. Однако исследования показывают, что при температурах близких к температуре плавления в ГЦК металле не более 20% от общего числа вакансий связывается в дивакансии. Расчеты показывают, что энергия миграции дивакансии в двое меньше, чем энергия миграции моновакансий. Следовательно, дивакансии должны быть более подвижные, это можно показать на следующей схеме дивакансий. 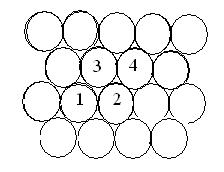Ранее было показано, что для перемещения основного атома в вакантное место, ему необходимо преодолеть

потенциальный барьер. В случае дивакансии атома 3 в положение 1 никаких затруднений нет, таким образом дивакансия легко мигрирует путем поочередного перехода в неё одного из соседних атомов. После перехода атома 3 в положение 1 дивакансия окажется в положение 2,3 , затем атом 4 положение 2 и дивакансия для 3,4. Считается, что дивакансии вносят заметный вклад в диффузионные процессы из-за своей большой подвижности. Так например энергия миграции моно, ди, три вакансии в золоте составляют 0,83; 0.7; 0.53 эВ соответственно. В ГЦК решётке энергетически выгодным является образование комплекса из четырёх вакансий. В центре которого имеется атом попавший при небольшом перемещение из узла решётки.

Т емные шары – вакансии. Получаем тетраэдрические вакансии.

Атом, который должен находиться в одной из вакансий, находиться в середине тетраэдра. Такой комплекс из четырех вакансий включает три вакансии как одну из граней тетраэдра.

Для миграции этого комплекса необходим возврат атома из центра тетраэдра на вершину куба и перемещение в центр тетраэдра другого соседнего атома. Из-за такого сложного процесса тетраэдрический комплекс из четырех вакансий рассматривается как неподвижный. Т. о. когда вакансия встречается с моновакансиями, образуя в конечном итоге тетраэдрический комплекс, они закрепляются на месте и перестают быть подвижными. Такие комплексы могут служить центрами «конденсации» других вакансий, образуя в конечном итоге вакансионные поры, т. е. крупные скопления вакансий. Однако нельзя думать, что, стремясь уменьшить поверхностную энергию, все вакансии должны слиться в одну пустоту. Это невозможно, т. к. такой переход от беспорядка к порядку в решетке должен сопровождаться резким понижением энтропии, а этого природа не допускает.