
- •1.Потенциал парного взаимодействия (Потенциал Леннарда - Джонса).
- •2. Агрегатное состояние вещества.
- •3. Жидкости и особенности их структуры.
- •4. Основные свойства жидкостей
- •5. Кристаллические и аморфные тела
- •6. Кристаллические тела и их структуры.
- •7. Дефекты кристаллического строения металлов
- •8. Точечные дефекты.
- •9. Межузельные пустоты в гцк решетке.
- •10. Межузельные пустоты в оцк и гп решетках.
- •12. Искажение решетки вокруг точечных дефектов.
- •13. Термодинамика точечных дефектов
- •14. Миграция точечных дефектов.
- •1Вакансии
- •2)Межузельные атомы.
- •15. Вакансионные комплексы.
- •16. Комплексы из межузельных атомов
- •17. Поведение вакансий при закалке
- •18. Методы определения концентрации вакансий, энергии образования и миграции.
- •2 Метод.
- •3 Метод.
- •19. Измерение энергии активации миграции вакансий.
- •20. Дислокации.
- •21. Краевые дислокации. Экстраплоскость. Ядро дислокации. Положительная и отрицательная дислокации, их обозначение.
- •22. Объяснение механизма скольжения краевой дислокации. Скорость скольжения краевой дислокации.
- •23. Переползание краевой дислокации. Пороги на краевой дислокации.
- •24.Винтовая дислокация. Отличие винтовой дислокации от краевой дислокации.
- •25. Скольжение винтовой дислокации.
- •26. Смешанные дислокации и их движения. Дислокационные петли.
- •27. Вектор Бюргерса
- •28. Энергия дислокаций. Вывод формулы энергии винтовой дислокации. Сравнение энергий винтовой и краевой дислокаций. Обсуждение формулы энергии дислокаций.
- •29. Взаимодействие параллельных краевых дислокаций.
- •30. Дислокационные стенки.
- •31. Взаимодействие параллельных винтовых дислокаций. Сила их взаимодействия.
- •32. Полные и частичные дислокации. Дислок. Реакции. Критерий Франка.
- •33. Плотнейшие упаковки
- •34. Дефекты упаковки
- •36. Характер теплового движения частиц в кристаллах.
- •37. Скорость упругих волн. Характеристики волн.
- •38. Колебательные моды линейной одноатомной цепочки.
- •39. Анализ закона дисперсии. Первая зона Бриллюэна.
- •40. Нормальные колебания линейной 2-х атомной цепочки.
- •41. Анализ закона дисперсии для двухатомной цепочки.
- •42. Акустическая и оптическая ветви двухатомной цепочки.
- •Оптическая ветвь
- •43. Колебания атомов в трехмерном одноатомном кристалле.
- •44. Классическая теория теплоёмкости кристалла. Её недостатки. Закон Дюлонга-Пти.
- •45 .Эйнштейновская теория теплоёмкости. Вывод формулы для средней энергии осциллятора. Анализ теории.
- •46. Дебаевская теория теплоемкости кристаллической решетки. Вывод формулы.
- •47. Анализ уравнения Дебая. Температура Дебая.
- •48. Теплопроводность твердых тел
- •49. Ангармонические эффекты. Тепловое расширение твёрдых тел.
10. Межузельные пустоты в оцк и гп решетках.
О ЦКP
не плотно упакована, К=0,68.
ЦКP
не плотно упакована, К=0,68.
Октаэдрическая пустота
Октаэдр сплюснутый (сжат), поэтому объём пустоты маленький.
Т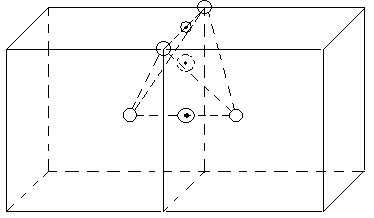 .о.
на этом рис. показано расположение
октаэдрической пустоты в ОЦКP.
Она oкружена
4-мя атомами в вершинах куба и 2-мя атомами
в центрах соседних кубов. Эта пустота
небольшая, т.к. атомы находящиеся в
центрах 2-х соседствующих эл. ячеек
сильно выступают друг к другу по
направлению к грани. В октопору можно
вписать шар R=
0,154•r
. В ОЦКP
октопора образуется ещё в серединах
рёбер. 12 октопор находится в серединах
ребер т.к. каждый из них одновременно
принадлежит 4-м эл-м ячейкам, то на одну
эл. ячейку приходится 3 октопоры. На 6-ти
гранях находится 6 октопор, каждая из
которых одновременно принадлежит 2-м
эл-м ячейкам, то на одну эл-ю ячейку
приходится 6 октопор. На 1 атом в ОЦКP
приходится 3 октопоры. Тетрапора в ОЦКP
окружена 4-мя атомами: 2-мя атомами в
вершинах куба и 2-мя атомами в центрах
2-х смежных эл-ых ячеек. Если на эл. ячейку
приходится 6 октопор, то тетрапор будет
12.=> на атом в ОЦКP
приходится 6 тетрапора. Объём тетрапор
в ОЦК>объёма октапор (в ГЦК наоборот).
В тетрапору ОЦК можно вписать шар R
= 0,291r
, но это все равно меньше чем размер
октапор в ГЦК. Меньший коэффициент
компактности ОЦКP
(большая рыхлость упаковки по сравнению
с ГЦК) обусловлен большим числом пустот.
.о.
на этом рис. показано расположение
октаэдрической пустоты в ОЦКP.
Она oкружена
4-мя атомами в вершинах куба и 2-мя атомами
в центрах соседних кубов. Эта пустота
небольшая, т.к. атомы находящиеся в
центрах 2-х соседствующих эл. ячеек
сильно выступают друг к другу по
направлению к грани. В октопору можно
вписать шар R=
0,154•r
. В ОЦКP
октопора образуется ещё в серединах
рёбер. 12 октопор находится в серединах
ребер т.к. каждый из них одновременно
принадлежит 4-м эл-м ячейкам, то на одну
эл. ячейку приходится 3 октопоры. На 6-ти
гранях находится 6 октопор, каждая из
которых одновременно принадлежит 2-м
эл-м ячейкам, то на одну эл-ю ячейку
приходится 6 октопор. На 1 атом в ОЦКP
приходится 3 октопоры. Тетрапора в ОЦКP
окружена 4-мя атомами: 2-мя атомами в
вершинах куба и 2-мя атомами в центрах
2-х смежных эл-ых ячеек. Если на эл. ячейку
приходится 6 октопор, то тетрапор будет
12.=> на атом в ОЦКP
приходится 6 тетрапора. Объём тетрапор
в ОЦК>объёма октапор (в ГЦК наоборот).
В тетрапору ОЦК можно вписать шар R
= 0,291r
, но это все равно меньше чем размер
октапор в ГЦК. Меньший коэффициент
компактности ОЦКP
(большая рыхлость упаковки по сравнению
с ГЦК) обусловлен большим числом пустот.
ГП решетка
В этой решетке как в ГЦК решетке на каждый атом приходится 2 тетрапоры и 1 октапора, в которые можно вписать сферы R = 0,22r и R = 0,41r , соответственно коэффициент компактности равен 0,7405 .
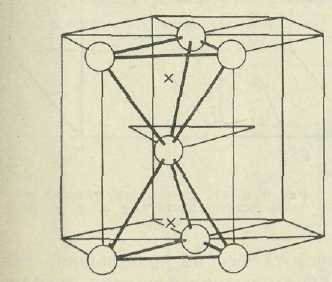 В
этом случае тетраэдрические поры
находятся между тремя атомами базисной
плоскости и одним атомом внутри объема
гексагональной призмы.
В
этом случае тетраэдрические поры
находятся между тремя атомами базисной
плоскости и одним атомом внутри объема
гексагональной призмы.
Если
внедряется атом с размером, превышающим
размер пустоты, то он должен раздвинуть
соседние атомы, при этом вокруг
тетраэдрической поры сразу смешивается
4 атома в направлении плотной упаковки,
что вызывает значительное перекрытие
взаимно отталкивающихся электронных
облаков. Вокруг октаэдрической поры
при этом смещаются 2 атома вдоль ребра
куба. Поэтому примесные атомы внедрения
в ОЦКP
могут легко размещаться в меньших по
размеру октаэдрических пор. Одиночные
межузельные атомы основного металла,
размещаясь в ц ентре
самой большой пустоты должны вызвать
очень сильное смещение соседей в ГЦК
решетке, таковыми являются октаэдрические
поры. Расчеты показывают, что вместо
одиночного межузельного атома находящегося
в октаэдрической пустоте ГЦК решетки
энергетически более выгодно стабильная
конфигурация из 2-х межузельных атомов.
Такую конфигурацию называют расщеплением
по направлению <100> или гантелью
[100].
ентре
самой большой пустоты должны вызвать
очень сильное смещение соседей в ГЦК
решетке, таковыми являются октаэдрические
поры. Расчеты показывают, что вместо
одиночного межузельного атома находящегося
в октаэдрической пустоте ГЦК решетки
энергетически более выгодно стабильная
конфигурация из 2-х межузельных атомов.
Такую конфигурацию называют расщеплением
по направлению <100> или гантелью
[100].
В центре грани должен находиться атом, а межузельный атом вытесняет его и образуется пара межузельных атомов, которая называется гантелью.
Атом в центре грани как бы расщепился на 2 межузельных атома, т.е. образовалась гантель. Энергия кристалла будет меньше, если образуется гантель.
В ОЦК решетке наиболее устойчивым, по сравнению с одиночным межузельным атомом, является гантель, но другого направления.
 <110>
В случае ОЦК решетки наиболее выгодным
является образование гантели в направлении
<110>. Атом в вершине элементарной
ячейки расщепляется в направлении
<110>. Лишний атом может создать так
же уплотненную цепочку атомов, которую
называют краудионом.
<110>
В случае ОЦК решетки наиболее выгодным
является образование гантели в направлении
<110>. Атом в вершине элементарной
ячейки расщепляется в направлении
<110>. Лишний атом может создать так
же уплотненную цепочку атомов, которую
называют краудионом.
 В
краудионе цепочка из n+1
атомов умещается на отрезке, где в
нормальном состоянии должны были
находиться n
атомов.
В
краудионе цепочка из n+1
атомов умещается на отрезке, где в
нормальном состоянии должны были
находиться n
атомов.
