
- •1.Потенциал парного взаимодействия (Потенциал Леннарда - Джонса).
- •2. Агрегатное состояние вещества.
- •3. Жидкости и особенности их структуры.
- •4. Основные свойства жидкостей
- •5. Кристаллические и аморфные тела
- •6. Кристаллические тела и их структуры.
- •7. Дефекты кристаллического строения металлов
- •8. Точечные дефекты.
- •9. Межузельные пустоты в гцк решетке.
- •10. Межузельные пустоты в оцк и гп решетках.
- •12. Искажение решетки вокруг точечных дефектов.
- •13. Термодинамика точечных дефектов
- •14. Миграция точечных дефектов.
- •1Вакансии
- •2)Межузельные атомы.
- •15. Вакансионные комплексы.
- •16. Комплексы из межузельных атомов
- •17. Поведение вакансий при закалке
- •18. Методы определения концентрации вакансий, энергии образования и миграции.
- •2 Метод.
- •3 Метод.
- •19. Измерение энергии активации миграции вакансий.
- •20. Дислокации.
- •21. Краевые дислокации. Экстраплоскость. Ядро дислокации. Положительная и отрицательная дислокации, их обозначение.
- •22. Объяснение механизма скольжения краевой дислокации. Скорость скольжения краевой дислокации.
- •23. Переползание краевой дислокации. Пороги на краевой дислокации.
- •24.Винтовая дислокация. Отличие винтовой дислокации от краевой дислокации.
- •25. Скольжение винтовой дислокации.
- •26. Смешанные дислокации и их движения. Дислокационные петли.
- •27. Вектор Бюргерса
- •28. Энергия дислокаций. Вывод формулы энергии винтовой дислокации. Сравнение энергий винтовой и краевой дислокаций. Обсуждение формулы энергии дислокаций.
- •29. Взаимодействие параллельных краевых дислокаций.
- •30. Дислокационные стенки.
- •31. Взаимодействие параллельных винтовых дислокаций. Сила их взаимодействия.
- •32. Полные и частичные дислокации. Дислок. Реакции. Критерий Франка.
- •33. Плотнейшие упаковки
- •34. Дефекты упаковки
- •36. Характер теплового движения частиц в кристаллах.
- •37. Скорость упругих волн. Характеристики волн.
- •38. Колебательные моды линейной одноатомной цепочки.
- •39. Анализ закона дисперсии. Первая зона Бриллюэна.
- •40. Нормальные колебания линейной 2-х атомной цепочки.
- •41. Анализ закона дисперсии для двухатомной цепочки.
- •42. Акустическая и оптическая ветви двухатомной цепочки.
- •Оптическая ветвь
- •43. Колебания атомов в трехмерном одноатомном кристалле.
- •44. Классическая теория теплоёмкости кристалла. Её недостатки. Закон Дюлонга-Пти.
- •45 .Эйнштейновская теория теплоёмкости. Вывод формулы для средней энергии осциллятора. Анализ теории.
- •46. Дебаевская теория теплоемкости кристаллической решетки. Вывод формулы.
- •47. Анализ уравнения Дебая. Температура Дебая.
- •48. Теплопроводность твердых тел
- •49. Ангармонические эффекты. Тепловое расширение твёрдых тел.
38. Колебательные моды линейной одноатомной цепочки.
Закон дисперсии. Вывод уравнения дисперсии.
О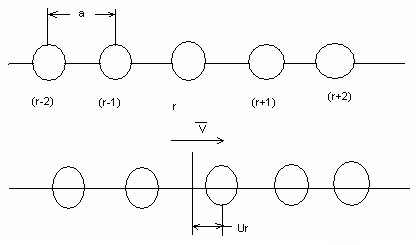 дноатомной
решетка –
кристалл, кот. состоит из атомов одного
сорта. В целях упрощения рассмотрим
линейную одноатомную цепь. Для простоты
рассмотрим распределение упругой
продольной волны вдоль линейной цепи,
состоящей из одинаковых атомов. Через
V
обозначим смещение атома от положения
равновесия в некоторый момент времени.
Запишем уравнение плоской волны:
дноатомной
решетка –
кристалл, кот. состоит из атомов одного
сорта. В целях упрощения рассмотрим
линейную одноатомную цепь. Для простоты
рассмотрим распределение упругой
продольной волны вдоль линейной цепи,
состоящей из одинаковых атомов. Через
V
обозначим смещение атома от положения
равновесия в некоторый момент времени.
Запишем уравнение плоской волны:
![]() (1)
(1)
А - амплитуда колебаний частиц участвующих в волновом процессе;
![]() -
волновой вектор (
-
волновой вектор (![]() );
);
![]() - угловая (циклическая) частота.
- угловая (циклическая) частота.
Атомы, имеющие массу m, расположены на расстоянии, а друг от друга. Для этой последовательности смещение атомов V, создаваемое волной, имеет смысл только в точках расположения атомов и не имеет смысла в промежуточных точках. Поэтому, смещение r-го атома записывается
![]()
Если
мы продифференцируем по времени 2 раза,
то получим ускорение r-го
атома:
![]() (3)
(3)
Т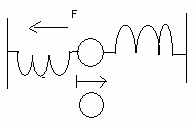 огда,
исходя из 2-го закона Ньютона, мы можем
записывать выражение для возвращающей
силы (упругой силы):
огда,
исходя из 2-го закона Ньютона, мы можем
записывать выражение для возвращающей
силы (упругой силы):
![]()
Наша задача: мы должны найти закон дисперсии.
Дисперсия - разложение света по спектрам. Почему разлагается спектр?
Т. к. Белый свет не монохроматичный.
![]() .
.
Для
получения закона дисперсии, т.е.
зависимости
от к,
надо выразить возвращающую силу
![]() через силовую постоянную, характеризующую
смещение атомов в кристаллической
решетки. В этих целях линейную цепочку
атомов представим в виде связанных
упругими пружинами:
через силовую постоянную, характеризующую
смещение атомов в кристаллической
решетки. В этих целях линейную цепочку
атомов представим в виде связанных
упругими пружинами:
В этой модели возникающая при растяжение
и сжатие пружин возвращающая сила,
действующая на атом линейно, зависит
от расстояния до ближайших атомов.
Действительно в большинстве твердых
тел в случае малых деформаций выполняется
закон Гука, тогда выражение для
возвращающей силы будет иметь вид:
этой модели возникающая при растяжение
и сжатие пружин возвращающая сила,
действующая на атом линейно, зависит
от расстояния до ближайших атомов.
Действительно в большинстве твердых
тел в случае малых деформаций выполняется
закон Гука, тогда выражение для
возвращающей силы будет иметь вид:
![]()
Сравнивая этот результат с выражением (4) получаем
![]()
Сюда подставим выражение (2)
![]()
Получили дисперсионное уравнение для продольных волн, распространяющихся вдоль линейной одноатомной цепочки, где учитывалось взаимодействие только с ближайшими соседями
![]()
Здесь знаки «+» и «-» соответствуют волнам, распространяющимся в противоположных направлениях от r-го атома.
39. Анализ закона дисперсии. Первая зона Бриллюэна.
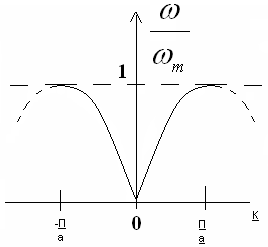
Приступим к анализу уравнения (8).
Кривая
представленная на этом рисунке будет
иметь такой же вид, если мы учитываем
взаимодействие атомов с ближайшими
соседями, но с более удаленными. В
уравнение (8) мы имеем зависимость
![]() от
от
![]() .
Обратим внимание на область малых к,
кот. соответствует области больших длин
волн, а большие длины волн соответствуют
макроскопической теории упругости.
.
Обратим внимание на область малых к,
кот. соответствует области больших длин
волн, а большие длины волн соответствуют
макроскопической теории упругости.
1)
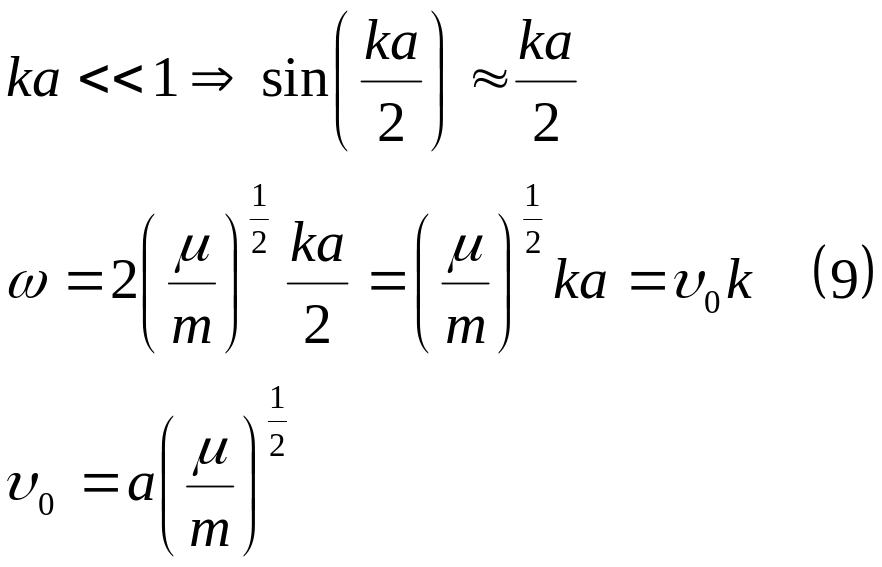
Вытекает, что в области больших или низких частот дисперсия отсутствует.
![]() ,
,
![]() - скорость звука;
- скорость звука;
![]() - фазовая скорость;
- фазовая скорость;
![]() никакой
дисперсии нет,
никакой
дисперсии нет,
![]() - групповая скорость.
- групповая скорость.
 ,
,
![]() - линейная плотность.
- линейная плотность.
Даже
в рамках грубой одномерной модели можно
рассчитать коэффициент жесткости
![]() ,
если известна скорость звука в данном
твердом теле.
,
если известна скорость звука в данном
твердом теле.
Модуль объемной упругости.
![]() (10)
,
(10)
,
![]()
Рассматриваемое
низкочастотное приближение справедливо
вплоть до
![]() Гц.
Гц.
2) Из приведенного графика видно, что по мере перехода по все более коротким волнам достигает предельного значения.
![]()
3) В области промежуточных частот происходит сильная дисперсия скорости звука. В общем виде зависимости фазовой и групповой скорости от к имеют вид:
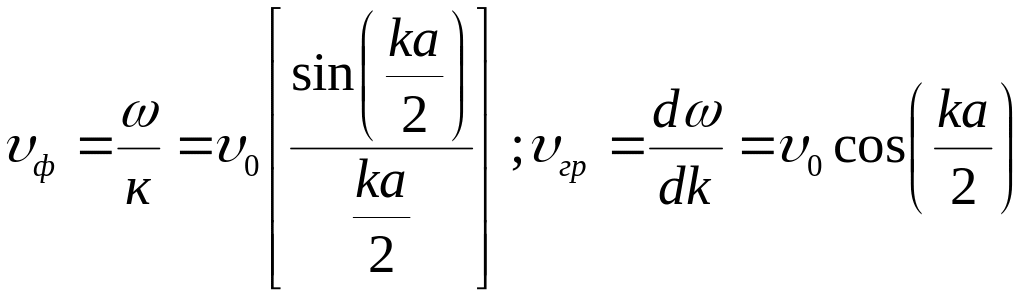 (11)
(11)
Из
(11) уравнения видно, что при
![]() или при
или при
![]() групповая скорость
групповая скорость
![]() .
При этом соседние атомы колеблются в
противоположных фазах.
.
При этом соседние атомы колеблются в
противоположных фазах.
4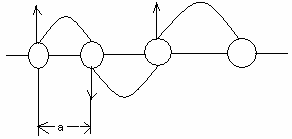 )Есть
участки кривой на рисунке изображение
штриховой линией. Эти участки не имеют
физического смысла, т.к.
)Есть
участки кривой на рисунке изображение
штриховой линией. Эти участки не имеют
физического смысла, т.к.
![]() нечему колебаться.
нечему колебаться.
Выше мы говорили, что в кристалле могут возникать упругие волны различных частот, колебания какой-то одной частоты наз. модой колебаний.
Т.о.
разрешенная и имеющая физический смысл
нормальные моды
колебаний
- это те волновые числа, которые заключены
в интервале
![]() .
.
Эту
область значений к
наз. первой зоной Бриллюэна одномерной
цепочки. Т.о. приходим к выводу, что
первая зона Бриллюэна содержит полный
спектр колебаний сосредоточенных в
этой области. Тот факт, что при
![]() групповая скорость = 0, говорит о том,
что на границе 1-ой зоны Бриллюэна
происходит отражение волны и образуется
стоячая волна. Полученное дисперсионное
уравнение и наши рассуждения не совсем
отражают действительность, поскольку
при выводе уравнения (8) мы сделали
предположение, что атомы взаимодействуют
только с ближайшими соседями. Если снять
это ограничение, то оказывается, что
решение остается неизменным по форме
и, более того, остаются справедливыми
условия, которые определяют и ограничивают
область разрешенных значений к.
Однако уравнение (8) оказывается не
совсем правильным, соответствующее ему
уравнение окажется более сложным по
форме и будет зависеть не только от
одной упругой постоянной. Тем не менее,
оно покажет переход к сплошной среде
при больших
и исчезновение
групповая скорость = 0, говорит о том,
что на границе 1-ой зоны Бриллюэна
происходит отражение волны и образуется
стоячая волна. Полученное дисперсионное
уравнение и наши рассуждения не совсем
отражают действительность, поскольку
при выводе уравнения (8) мы сделали
предположение, что атомы взаимодействуют
только с ближайшими соседями. Если снять
это ограничение, то оказывается, что
решение остается неизменным по форме
и, более того, остаются справедливыми
условия, которые определяют и ограничивают
область разрешенных значений к.
Однако уравнение (8) оказывается не
совсем правильным, соответствующее ему
уравнение окажется более сложным по
форме и будет зависеть не только от
одной упругой постоянной. Тем не менее,
оно покажет переход к сплошной среде
при больших
и исчезновение
![]() .
.
