29. Взаимодействие параллельных краевых дислокаций.

Вокруг дислокаций решетка деформирована и имеется поле упругих напряжений. Это поле упругих напряжений и является источником силы действующей на соседнюю дислокацию. Сила, действующая на единицу длины дислокации, равна произведению вектора Бюргерса на составляющую касательного напряжения в направлении этого вектора. В кристалле на каждый выделенный объем действует напряжение как нормальное, так и касательное.

Н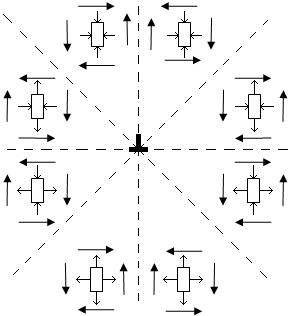 а рисунке схематично изображены нормальные и касательные напряжения в разных областях вокруг краевой дислокации. Выделено 8 областей при переходе через границы которых меняется знак напряжений. Поле напряжений вокруг краевой дислокации не обладает симметрией, как поле напряжений вокруг винтовой дислокации, с одной стороны имеет область всестороннего сжатия, с другой стороны область всестороннего растяжения.

Изображение поля распространяется дальше от дислокаций, пока не встретиться с полем напряжений соседней дислокации. Это взаимодействие встречающихся полей приводит к взаимодействию дислокаций. Для анализа сил взаимодействия дислокаций являются более важные касательные напряжения, действующие в плоскости скольжения. В поле напряжений вокруг краевых дислокаций в точке с координатами х и у касательное напряжение в плоскости параллельное плоскости скольжения будет: ,

где х - координата в направлении вектора Бюргерса,

у – координата в направлении перпендикулярном плоскости скольжения.

30. Дислокационные стенки.

Взаимодействие одноименных и разноименных дислокаций.

Рассмотрим 2 дислокации одного знака расположенные в параллельных плоскостях скольжения. Сила воздействия первой дислокации, находящейся в точке О на вторую дислокацию имеющую координаты (х,у) в параллельной плоскости скольжения:

С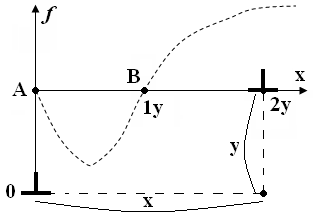 ложный характер зависимости этой силы от х обусловлен отмеченной выше асимметрией поля напряжений вокруг краевой дислокации. Здесь показана зависимость силы взаимодействия 2-х дислокаций от расстояния между ними в направлении скольжения. Для удобства анализа за 1 длины в направлении х принята величина у. Как видно правее от т.В сила является положительной, а между точками А и В она отрицательна. Положительная сила соответствует отталкиванию, а отрицательная –притягиванию соответствующих дислокаций. В т.В х=у, следовательно f=0. в точке А х=0, следовательно f=0. Стало быть, когда две дислокации находятся в т.В, то система в равновесии.

Правее в т.В х>0, х>у, f >0, т.е. одноименные дислокации взаимно отталкиваются. Левее т.В х<у, х<0 –это говорит о том, что краевые дислокации взаимно притягиваются. Такие дислокации приводят к Сила взаимодействия одноименных дислокаций равна 0, при х=0 в т.А и при х=у в т.В. в этих точках дислокации находятся в равновесии, но в точке В будет неустойчивое равновесие, поскольку при от отклонении от нее вправо или влево возникает сила отталкивания. Зато в т.А равновесие устойчивое, небольшое отклонение от т.А приводит к возникновению силы, стремящейся вернуть дислокацию обратно в эту точку.

Т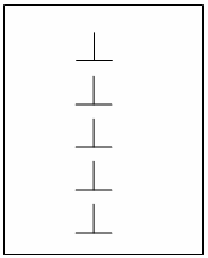 .о. краевые дислокации одного знака расположенные одна над другой образуют механическую устойчивую конфигурацию, если в кристалле имеется несколько одноименных дислокаций на достаточно близких плоскостях скольжения, то они благодаря взаимному притяжению, одна над другой и образуют так называемую дислокационную стенку. Между одноименными дислокациями, находящимися в одной плоскости скольжения, действует отталкивающая сила. Отсутствие взаимного притяжения в этом случае, объясняется тем, что при сближении 2-х экстраплоскостей происходит возникновение чрезвычайно сильного искажения решетки.

Рассмотрим взаимодействие разноименных краевых дислокаций, расположенных в параллельных плоскостях скольжения. В этом случае сила воздействия дислокаций находится в т.О на дислокацию противоположного знака с координатами (х,у) определяется формулой:

Следовательно, график зависимости f(x) будет иметь перевёрнутый вид. При х>у следовательно, они отталкиваются.

П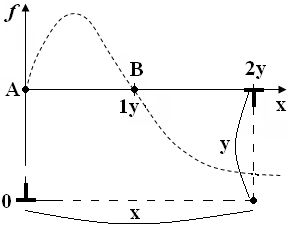 ри х=0 и х=у следовательно f=0. однако в точке А равновесие будет неустойчивое.

Так что при небольшом отклонении от т. А дислокации необратимо отдаляются друг от друга. В т.В равновесие будет устойчивое.

Если одноименные дислокации находятся в одной плоскости скольжения у=0, то между ними действует только сила

f= - [Cb²…] –это сила притяжения.

Когда сближающиеся в одной плоскости скольжения дислокации подходят друг к другу, они аннигилируют. Такую аннигиляцию можно представить как слияние атомов в одну атомную плоскость.