
- •1.Потенциал парного взаимодействия (Потенциал Леннарда - Джонса).
- •2. Агрегатное состояние вещества.
- •3. Жидкости и особенности их структуры.
- •4. Основные свойства жидкостей
- •5. Кристаллические и аморфные тела
- •6. Кристаллические тела и их структуры.
- •7. Дефекты кристаллического строения металлов
- •8. Точечные дефекты.
- •9. Межузельные пустоты в гцк решетке.
- •10. Межузельные пустоты в оцк и гп решетках.
- •12. Искажение решетки вокруг точечных дефектов.
- •13. Термодинамика точечных дефектов
- •14. Миграция точечных дефектов.
- •1Вакансии
- •2)Межузельные атомы.
- •15. Вакансионные комплексы.
- •16. Комплексы из межузельных атомов
- •17. Поведение вакансий при закалке
- •18. Методы определения концентрации вакансий, энергии образования и миграции.
- •2 Метод.
- •3 Метод.
- •19. Измерение энергии активации миграции вакансий.
- •20. Дислокации.
- •21. Краевые дислокации. Экстраплоскость. Ядро дислокации. Положительная и отрицательная дислокации, их обозначение.
- •22. Объяснение механизма скольжения краевой дислокации. Скорость скольжения краевой дислокации.
- •23. Переползание краевой дислокации. Пороги на краевой дислокации.
- •24.Винтовая дислокация. Отличие винтовой дислокации от краевой дислокации.
- •25. Скольжение винтовой дислокации.
- •26. Смешанные дислокации и их движения. Дислокационные петли.
- •27. Вектор Бюргерса
- •28. Энергия дислокаций. Вывод формулы энергии винтовой дислокации. Сравнение энергий винтовой и краевой дислокаций. Обсуждение формулы энергии дислокаций.
- •29. Взаимодействие параллельных краевых дислокаций.
- •30. Дислокационные стенки.
- •31. Взаимодействие параллельных винтовых дислокаций. Сила их взаимодействия.
- •32. Полные и частичные дислокации. Дислок. Реакции. Критерий Франка.
- •33. Плотнейшие упаковки
- •34. Дефекты упаковки
- •36. Характер теплового движения частиц в кристаллах.
- •37. Скорость упругих волн. Характеристики волн.
- •38. Колебательные моды линейной одноатомной цепочки.
- •39. Анализ закона дисперсии. Первая зона Бриллюэна.
- •40. Нормальные колебания линейной 2-х атомной цепочки.
- •41. Анализ закона дисперсии для двухатомной цепочки.
- •42. Акустическая и оптическая ветви двухатомной цепочки.
- •Оптическая ветвь
- •43. Колебания атомов в трехмерном одноатомном кристалле.
- •44. Классическая теория теплоёмкости кристалла. Её недостатки. Закон Дюлонга-Пти.
- •45 .Эйнштейновская теория теплоёмкости. Вывод формулы для средней энергии осциллятора. Анализ теории.
- •46. Дебаевская теория теплоемкости кристаллической решетки. Вывод формулы.
- •47. Анализ уравнения Дебая. Температура Дебая.
- •48. Теплопроводность твердых тел
- •49. Ангармонические эффекты. Тепловое расширение твёрдых тел.
19. Измерение энергии активации миграции вакансий.
Энергию
активации миграции вакансий Ем
определяют, анализируя кинетику изменения
электросопротивления при отжиге после
закалки. Падение электросопротивления
пропорционально снижению концентрации
вакансий
![]() ,т.е.
,т.е.
![]() .
Если за снижение электросопротивления
ответственен единственный термоактивированный
процесс с постоянной энергией активации,
которую можно принять за энергию
активации миграции вакансий Ем,
то скорость падения электросопротивления:
.
Если за снижение электросопротивления
ответственен единственный термоактивированный
процесс с постоянной энергией активации,
которую можно принять за энергию
активации миграции вакансий Ем,
то скорость падения электросопротивления:
![]() (1),
где
(1),
где
 По
экспериментальным данным строят
зависимость электросопротивления
от времени отжига t
при нескольких температурах, быстро
нагревая до этих температур закаленные
образцы.
По
экспериментальным данным строят
зависимость электросопротивления
от времени отжига t
при нескольких температурах, быстро
нагревая до этих температур закаленные
образцы.
И нтегрируя
уравнение (1), получаем
нтегрируя
уравнение (1), получаем
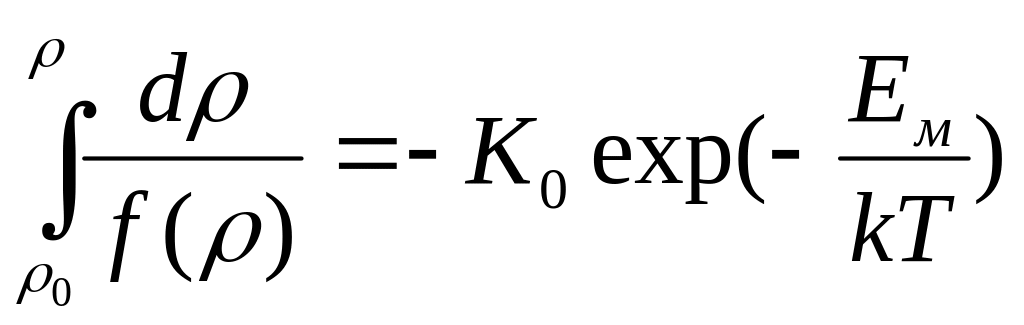 Проведем
параллельно оси абсцисс прямую при
произвольном значении
Проведем
параллельно оси абсцисс прямую при
произвольном значении
![]() .
Время достижения этого значения
электросопротивления зависит от
температуры отжига. Левая часть уравнения
при
.
Время достижения этого значения
электросопротивления зависит от
температуры отжига. Левая часть уравнения
при
![]() -
постоянная и не зависит от температуры
отжига:
-
постоянная и не зависит от температуры
отжига:
![]() Следовательно:
Следовательно:
![]() откуда
откуда![]()
20. Дислокации.
Дислокации - линейные несовершенства кристалла. В настоящие время теория дислокаций применяться для анализа самых разнообразных явлений в металлах и сплавах.
Деформация бывает упругая и пластичная. Упругая связана с обратимыми процессами, а пластичная с необратимыми.
Чистые монокристаллы многих твердых тел пластически легко деформируются. AgCl плавится при 1455°С, а при комнатой температуре это вещество пластично.
Теор. оценки предела упругости идеальных кристаллов приводят к значениям в 103-105 раз превышающем наблюдаемое на опыте.
Френкель дал простой метод оценки теоретического значения сопротивления сдвигу в совершенном кристалле.
Рассмотрит
его метод. 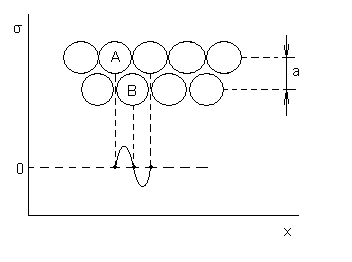
В ходе смешения до тех пор пока атом А не окажется непосредственно над атомом В напряжение вначале возрастает затем падает.
Френкель предложил модель одновременного сдвига всех атомов в верхней части кристалла относительно его неподвижной части.
По
этой модели напряжение σ сначала
увеличивается, потом падает до 0. Как
только атомные плоскости сдвинутся на
одно межат. расстояние а. Следовательно,
в промежутке 0≤x≤a
значения напряжения проходят через
max.
То же самое будет повторяться в промежутке
от a
до 2a
и т.д., отсюда выходит, что σ должна быть
периодичной функций x:
![]() ,
(1)
,
(1)
В
области малых x:
![]() ,а
в области малых x
выполняется закон Гука:
,а
в области малых x
выполняется закон Гука:
![]() ,
G-модуль
упругости (2)
,
G-модуль
упругости (2)
![]() ,
(1’). Сравниваем (1’) и (2),
,
(1’). Сравниваем (1’) и (2),
![]() ,
(3)
,
(3)
Т.
о.
![]() ,т.е.
составляет 1/6 часть модуля сдвига.
,т.е.
составляет 1/6 часть модуля сдвига.
Приведем несколько примеров.
|
σm, МПа, теорет. |
σ,МПа, эксперим. |
Cu |
1540 |
1,0 |
Ni |
2000 |
5,8 |
Fe |
2300 |
29,0 |
 Видно
модель одновременного скольжения всех
атомов по плоскости не пригодна.
Расхождение теор. и экспер. знач-ий
удалось объяснить существованием
специфических дефектов, а именно
дислокации. Для понимания их сущности
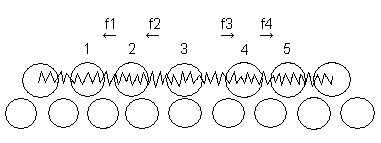
рассмотрим так называемую роликовую
модель.
Видно
модель одновременного скольжения всех
атомов по плоскости не пригодна.
Расхождение теор. и экспер. знач-ий
удалось объяснить существованием
специфических дефектов, а именно
дислокации. Для понимания их сущности
рассмотрим так называемую роликовую
модель.
В нормальной бездефектной структуре ролики верхнего ряда лежат в лунках м\у роликами нижнего ряда. В модели с дефектом 5 пронумерованных роликов верхнего ряда располагаются с искажением. Ролик 1 чуть сместился от своего норм. положения вправо из-за того, что все ролики связаны между собой упругими силами. Ролик 2 переместился ещё правее от своего положения и ролик 3 оказался под роликом нижнего ряда и т.д. Слева от ролика 1 и справа от ролика 5 все остальные ролики верхнего ряда располагаются в соответствующих лунках нижнего ряда как и подобает без дефектному ряду. В области дефекта 1-5 возникает силы f1 и f2, стремящиеся вернуть ролики 1 и 2 в левые лунки и силы f4 и f5, возвращающие 4 и 5 в правые лунки.
Согласно 3-му з-ну Ньютона |f1+ f2|=| f4+ f5| , поэтому вся система находится в равновесии. Стоит изменить равновесие сил слабым внеш. воздействием, и верхний ряд роликов переместится в сторону действия внешней силы. На этой модели видно почему кристалл, содержащий дислокацию легко деформируется под слабым внешним воздействием.
