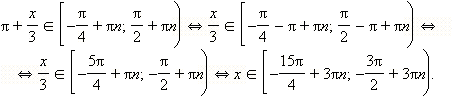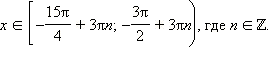3.2.4. Неравенства с модулем
Основные способы решений неравенств с модулем во многом совпадают с методами решения аналогичных уравнений. Единственное отличие, пожалуй, связано с тем, что, решая неравенства с модулем (как, впрочем, и неравенства вообще), нужно очень внимательно совершать равносильные переходы и следить не только за тем, чтобы не приобрести новые решения, но и за тем, чтобы не потерять уже имеющиеся.
Стандартный путь решения неравенств с модулем заключается в том, что координатная прямая разбивается на промежутки (границами этих промежутков являются нули подмодульных выражений), а затем неравенство решается на каждом из промежутков.
Этот метод работает всегда. Правда, в отдельных случаях может быть затруднена его техническая реализация, например, очень тяжело или невозможно найти корни подмодульных выражений и пр. Однако, это сложности иного плана. Нужно понимать, что раскрытие модуля по определению неизменно приводит к цели. Конечно же, этот метод не является оптимальным: в условиях конкурсного экзамена важен не только результат, но и то время, которое потрачено на его получение.
Рассмотрим методы, не связанные с поиском нулей функций, стоящих под знаком модуля.
Рассмотрим
неравенство
![]() Очевидно,
что те x, для которых g (x) < 0, не
являются решениями. Значит, если x
является решением, то для него g (x) ≥ 0,
и согласно геометрическому смыслу
модуля, как расстоянию на координатной
оси, данное неравенство равносильно
системе
Очевидно,
что те x, для которых g (x) < 0, не
являются решениями. Значит, если x
является решением, то для него g (x) ≥ 0,
и согласно геометрическому смыслу
модуля, как расстоянию на координатной
оси, данное неравенство равносильно
системе
![]() Таким
образом, имеем
Таким
образом, имеем
|
Аналогично
можно рассмотреть неравенство
![]() Неравенство
выполнено для тех x, для которых g (x) < 0
и функции f (x) и g (x) определены. Для
тех x, для которых g (x) ≥ 0, имеем
равносильную совокупность
Неравенство
выполнено для тех x, для которых g (x) < 0
и функции f (x) и g (x) определены. Для
тех x, для которых g (x) ≥ 0, имеем
равносильную совокупность

|
Заметим, что последняя совокупность является равносильной нашему неравенству и при g (x) ≤ 0. В этом можно непосредственно убедиться, учтя g (x) ≤ 0 и вспомнив определение знака совокупности.
Пример 1
Решите
неравенство
![]()
Решение
Перейдём к равносильной совокупности.
Ответ. |
Как видно, в простых случаях особых преимуществ метод перехода к равносильной системе не имеет, но иногда его преимущества весьма заметны.
Пример 2
Решите
неравенство
![]()
Решение
Как видно, найти значения x, при которых подмодульное выражение обращается в нуль, чрезвычайно затруднительно. Однако переход к равносильной системе значительно упрощает дело. Имеем:
Ответ. |
3.2.5. Тригонометрические неравенства
При
решении тригонометрических неравенств
вида f (x) ≥ 0, где f (x) − одна
из тригонометрических функций, удобно
использовать тригонометрическую
окружность для того, чтобы наиболее
наглядно представить решения неравенства
и записать ответ. Основным методом
решения тригонометрических неравенств
является сведение их к простейшим
неравенствам типа
![]() Разберём
на примере, как решать такие неравенства.
Разберём
на примере, как решать такие неравенства.
Пример 1
Решите
неравенство
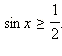
Решение
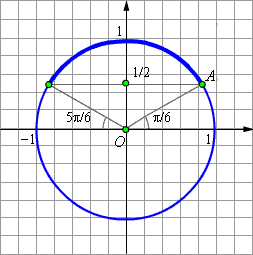
Нарисуем
тригонометрическую окружность и
отметим на ней точки, для которых
ордината превосходит
Для
x
[0; 2π]
решением данного неравенства будут
Ответ. где |
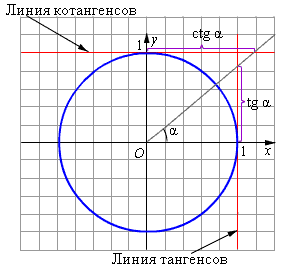
Для решения неравенств с тангенсом и котангенсом полезно понятие о линии тангенсов и котангенсов. Таковыми являются прямые x = 1 и y = 1 соответственно, касающиеся тригонометрической окружности.
|
Рисунок 3.2.5.1 |
Легко заметить, что если построить луч с началом в начале координат, составляющий угол α с положительным направлением оси абсцисс, то длина отрезка от точки (1; 0) до точки пересечения этого луча с линией тангенсов в точности равна тангенсу угла, который составляет этот луч с осью абсцисс. Аналогичное наблюдение имеет место и для котангенса.
|
Пример 2
Решите
неравенство
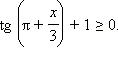
Решение
Обозначим
Ответ. Неравенства с обратными тригонометрическими функциями удобно решать с использованием графиков обратных тригонометрических функций. Покажем, как это делается на примере. |
Пример 3
Решите
неравенство
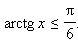
Решение
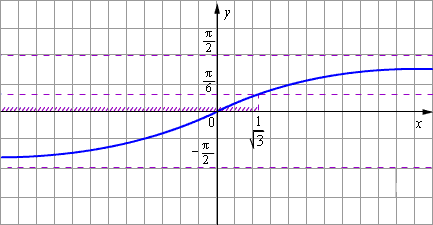
Нарисуем
график функции y = arctg x. Найдём
точку пересечения этого графика с
горизонтальной прямой
Ответ. |

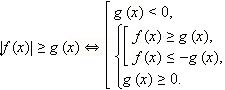
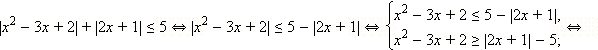
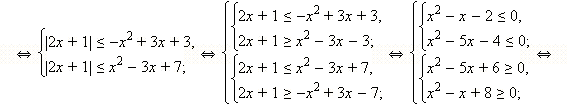
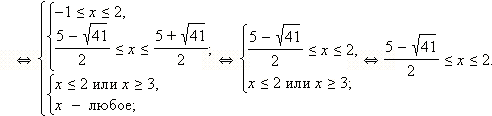
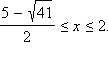
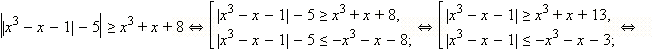
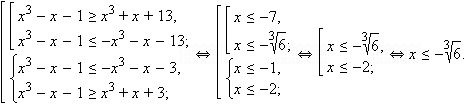
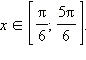 Ясно
также, что если некоторое число x будет
отличаться от какого-нибудь числа из
указанного интервала на 2πn,
Ясно
также, что если некоторое число x будет
отличаться от какого-нибудь числа из
указанного интервала на 2πn, 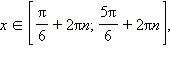 где
где
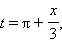 тогда
неравенство примет вид простейшего:
tg t ≥ –1. Рассмотрим интервал
тогда
неравенство примет вид простейшего:
tg t ≥ –1. Рассмотрим интервал
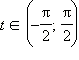 длиной,
равной наименьшему положительному
периоду (НПП) тангенса. На этом отрезке
с помощью линии тангенсов устанавливаем,
что
длиной,
равной наименьшему положительному
периоду (НПП) тангенса. На этом отрезке
с помощью линии тангенсов устанавливаем,
что
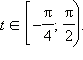 Вспоминаем
теперь, что необходимо добавить πn,
где
Вспоминаем
теперь, что необходимо добавить πn,
где
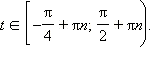 Возвращаясь
к переменной x, получаем, что
Возвращаясь
к переменной x, получаем, что