
- •Задачи по дисциплине «теоретические основы электротехники» Раздел «линейные цепи»
- •1. Основные законы, элементы и параметры электрических цепей
- •2 Электрическая цепь однофазного синусоидального тока
- •3 Применение комплексных чисел и векторных диаграмм к расчету электрических цепей
- •4 Резонанс в электрических цепях
- •5. Цепи трехфазного тока
- •6. Расчет цепей несинусоидального переменного тока
- •6.1 Способы предоставления несинусоидальных функций.
- •6.2 Энергетические характеристики несинусоидального тока
- •6.3 Расчет цепей несинусоидального переменного тока по мгновенным значениям
- •6.4 Расчет цепей несинусоидального переменного тока по комплексным значениям
- •Библиографический список
6. Расчет цепей несинусоидального переменного тока
6.1 Способы предоставления несинусоидальных функций.
При расчете цепей несинусоидального переменного тока используется разложение периодических функций в одну из форм гармонического ряда Фурье. Если периодическая негармоническая функция представляется суммой мгновенных значений гармонических колебаний различных частот ωκ=κω1, где κ=1,2,… порядковый номер гармоники ω1=2π/Т, то ряд Фурье записывают в следующем виде:

 где
где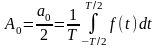
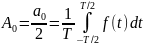 –постоянная
составляющая функции f(t),
равная ее среднему за период Т значению;
–постоянная
составляющая функции f(t),
равная ее среднему за период Т значению;
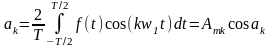 и
и
 —коэф-
—коэф-
фициенты ряда Фурье, соответствующие амплитудам гармоник квадратурных составляющих;
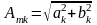 —
амплитуда
k-й
гармоники;
—
амплитуда
k-й
гармоники;
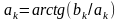 —
начальная
фаза k-й
гармоники.
—
начальная
фаза k-й
гармоники.
Если же расчет цепи производится по комлексным значениям, при разложении функции используют ряд Фурье в комплексной форме
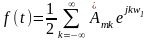 ,
,
где
 -комплексная
амплитуда
-комплексная
амплитуда
k-й гармоники.
Поскольку при разложении функции в ряд Фурье использовалась косинусная форма, то связь между комплексным рядом Фурье и разложением по мгновенным значениям устанавливается формулой:
 .
.
Зависимости Amk и ak от порядкового номера k-й гармоники (или от ее частоты kw1) принято называть амплитудным и фазовым спектрами колебания соответственно. Для периодических несинусоидальных колебаний амплитудный и фазовый спектры имеют дискретный характер, а расстояние по оси частот между смежными спектральными линиями равно w1. Теоретически ряд Фурье содержит бесконечное число членов, однако в большинстве практических случаев этот ряд достаточно быстро сходится, и при расчетах можно ограничиться сравнительно небольшим числом гармоник.
6.2 Энергетические характеристики несинусоидального тока
При расчете энергетических характеристик в цепях несинусоидального периодического тока используют следующие величины:
►►│ действующие значения напряжения U и тока I;
►►│ среднюю мощность P;
►►│ реактивную Q и полную S мощности;
►►│ мощность искажений D;
►►│ коэффициент искажений kD;
►►│ коэффициент мощности км.
Действующие значения напряжения и тока определяют как геометрическую сумму действующих значений отдельных гармоник:
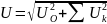 ;
;
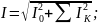
где
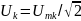
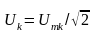 -
действующее значение k-й
гармоники
напряжения;
-
действующее значение k-й
гармоники
напряжения;
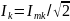
 -
действующее значение k-й
гармоники тока;
-
действующее значение k-й
гармоники тока;
U0, I0 - постоянные составляющие напряжения и тока, соответственно.
Среднюю
мощность несинусоидального
тока определяют как сумму мощностей
отдельных гармоник:

где
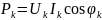 —
средняя мощность k-й
гармоники
тока;
—
средняя мощность k-й
гармоники
тока;
 —
мощность
постоянного тока.
—
мощность
постоянного тока.
Полную мощность несинусоидального тока определяют аналогично полной мощности синусоидального тока по формуле
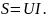
По аналогии с синусоидальным током вводится понятие реактивной мощности

где
 —
реактивная мощность k-й
гармоники
тока.
—
реактивная мощность k-й
гармоники
тока.
В отличие от синусоидального тока полная мощность S оказывается больше геометрической суммы средней и реактивной мощностей
 ;
;
поэтому разность этих мощностей носит название мощности искажений:

Отношение мощности искажений D к полной мощности S характеризует отклонение формы тока от формы напряжения и называется коэффициентом искажений

Коэффициент мощности в цепи несинусоидального тока определяют, так же как в цепи синусоидального тока, по формуле
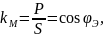
где
 -
угол сдвига фаз эквивалентного
синусоидального тока.
-
угол сдвига фаз эквивалентного
синусоидального тока.
Таким
образом, при определении большинства
энергетических характеристик
несинусоидального тока используется
понятие эквивалентного по мощности
синусоидального тока. Исключение
составляют мощность искажений и
коэффициент искажений, которые
характеризуют отличие формы напряжения
от формы тока. Для синусоидального тока
 ,
так как формы напряжения и тока одинаковы.
,
так как формы напряжения и тока одинаковы.
