ВАРИАНТ 1

Задача 1.

С целью исследования качества деталей на предприятии проверена партия из 100 деталей.

Вес деталей, г.	До 50	50-60	60-70	70-80	80-90	Свыше 90
Число деталей	7	17	30	31	8	7

Определите:

1) моду и медиану веса деталей;

2) дисперсию и коэффициент вариации веса деталей.

Решение:

1. Мода – наиболее часто встречающееся значение признака. Для дискретного ряда распределения мода определяется визуально. В данном случае наиболее представительной группой является группа деталей весом 70-80гр таких деталей 31 шт., значит данная группа деталей и будет модальным интервалом.

Мода =

где Хмо – нижняя граница медианного интервала

i - величина модального интервала

f₂ - частота модального интервала

f₃ - частота интервала следующего за модальным

f₁- частота интервала, предшествующего модальному

Мода = г.

Медиана – значение признака у единицы, которая делит ранжированный ряд пополам. (100/2=50, т.е. это значение признака 50 детали; 50 деталь попадает в интервал деталей с весом 60-70 г., значит этом интервал и будет медианным)

Медиана =

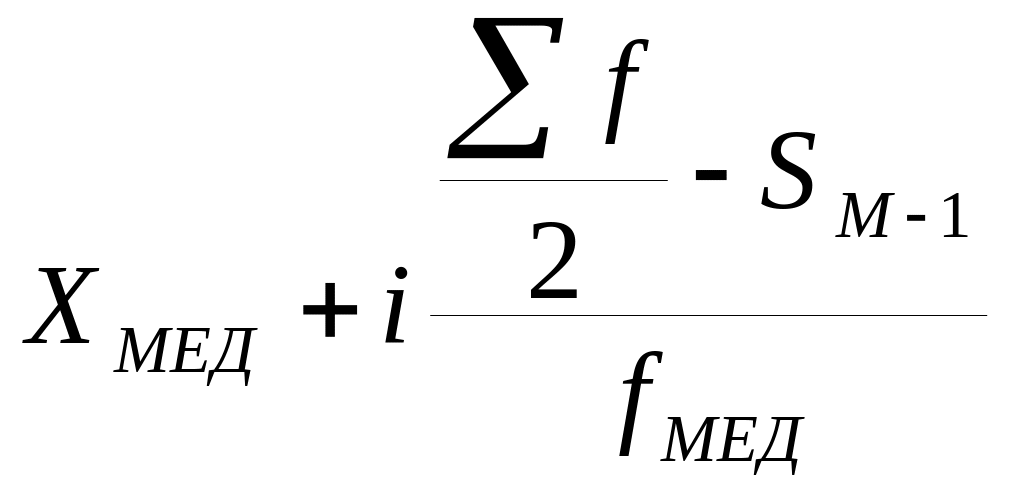
где Хмед – нижняя граница модального интервала

i - величина медианного интервала

Σf – сумма частот

S_М-1 - сумма накопленных частот до медианного интервала;

fмед - частота медианного интервала.

Медиана =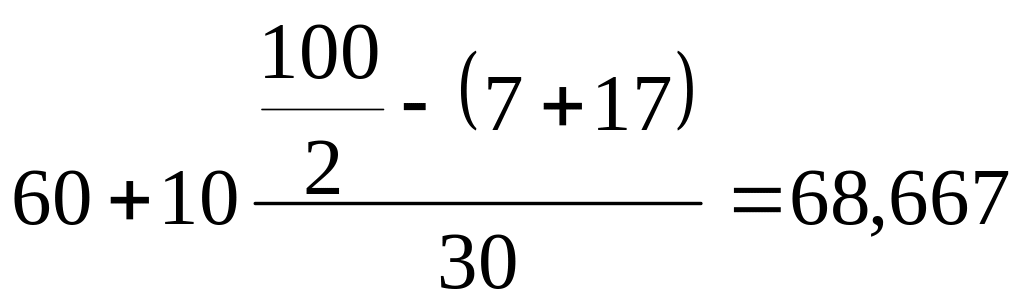 г.

Т.е. у единицы, которая делит ранжированный ряд пополам, вес составляет 68,667г.., вес наиболее часто встречающейся детали – 70,417г.

2. Определим дисперсию и коэффициент вариации веса деталей.

Средний квадрат отклонения (дисперсия) определяется по формуле:

Среднее квадратическое отклонение

Коэффициент вариации

Средний вес детали определим, используя формулу средней арифметической взвешенной:

где х – значение признака в каждой группе;

f - частота значения признака.

Все расчеты для нахождения среднего веса детали, дисперсии целесообразнее провести в табличной форме (как в случае с кореляционно-регриссионным анализом). Для этого прежде всего перейдем от модального ряда представления информации к дискретному.

Таблица 2- Промежуточные расчеты для нахождения дисперсии

х	f	xf			f
45	7	315	-23,7	561,69	3931,83
55	17	935	-13,7	187,69	3190,73
65	30	1950	-3,7	13,69	410,7
75	31	2325	6,3	39,69	1230,39
85	8	680	16,3	265,69	2125,52
95	7	665	26,3	691,69	4841,83
	100	 6870			 15731

г.

г.

или 18,26%

Поскольку исчисленный нами коэффициент вариации меньше 33%, то можем утверждать, что изучаемая нами совокупность однородна.

Задача 2.

Район	Число отделений банка	Среднее число вкладов в отделении	Средний размер вклада, млн. руб.
1	4	1376	2,75
2	9	1559	2,93
3	5	1315	2,68

Определите средний размер вклада в целом городу.

Решение

Средний размер вклада определим, используя формулу средней арифметической взвешенной:

где х – значение признака в каждой группе;

f - частота значения признака.

Однако в данном случае частота признака будет представлена у нас произведением числа отделений банка на среднее число вкладов в отделении.

млн.руб.

Итак, средний размер вклада в целом городу составил 2,83 млн.руб.

Задача 3.

Динамика себестоимости и объемы производства продукции характеризуется следующими данными:

Продукция	Произведено, шт.		Себестоимость одного изделия, руб.
	Базисный	Отчетный	Базисный	Отчетный
	период	период	период	период
А	1500	1800	0,8	0,95
Б	700	1100	3,02	2,8

Определите общий индекс затрат на производство, общий индекс себестоимости, общий индекс физического объема произведенной продукции. Определите абсолютное изменение затрат на производство в отчетном периоде по сравнению с базисным периодом и разложите его по факторам (за счет изменения себестоимости и за счет изменения объема производства продукции).

Решение

а) общий индекс затрат определи по формуле

I_qz. = I_qz. =

Итак, затраты увеличились в отчетном периоде по отношению к базисному на 44,54%

в) общий индекс себестоимости определим по формуле

I_z. = I_z. =

Средняя себестоимость продукции в отчетном периоде увеличилась на 1,44%

с) общий индекс физического объема продукции определим по формуле

I_q. = I_q. =

Объем производства в отчетном периоде увеличился на 42,48%

Между исчисленными индексами существует взаимосвязь I_qz. = I_z∙ I_q

1,4248*1,0144=1,4454, тождестово верно, значит вычисления выполнены верно

Разность меду числителем и знаменателем исчисленного нами выше индекса затрат представляет собой абсолютное изменение затрат на производство в отчетном периоде по сравнению с базисным периодом:

zq=4790-3314=1476 руб., в том числе

zq (z)=4790-4722=68 руб.

zq (q)=4722-3314=1408 руб.

Проверим правильность вычислений методом балансовой увязки:

zq=zq (z)+ zq (q)

1476=1408+68, тождестово верно, значит вычисления выполнены верно

Таким образом, затраты увеличились в отчетном периоде по отношению к базисному на 44,54% или на 1476 руб., в том числе в результате

• Роста средней себестоимость продукции в отчетном периоде на 1,44% объем затрат увеличился на 68 руб.

• Роста объема производства в отчетном периоде на 42,48% объем затрат увеличился на 1408 руб.