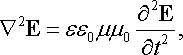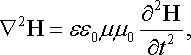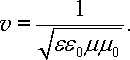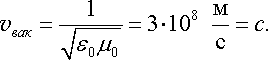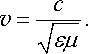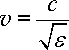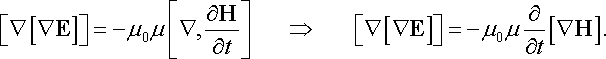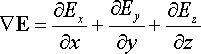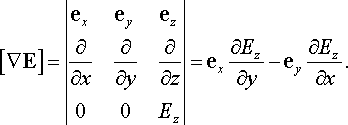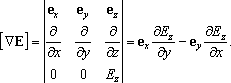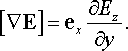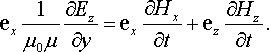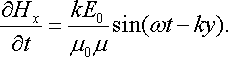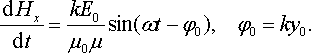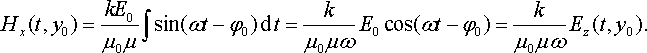41. Хвильове рівняння для електромагнітної хвилі. Доведення поперечності електромагнітної хвилі. Електромагнітні хвилі

З  рівнянь Максвелла (19.8), (19.9), (19.10), (19.11) видно, що змінне електричне поле породжує змінне магнітне поле, а змінне магнітне поле породжує змінне електричне поле. Тому, бувши первісно створені зарядами або струмами, змінні електричне та магнітне поля можуть далі самовідтворюватися й існувати автономно, незалежно від зарядів і струмів. Більше того, із рівнянь Максвелла випливає, що цей процес не лишається локалізованим у місці виникнення, а поширюється в просторі з плином часу. Це означає, що змінне електромагнітне поле у вільному просторі існує у формі електромагнітних хвиль. Максвелл також показав, що швидкість поширення електромагнітних хвиль співпадає із швидкістю світла, чим теоретично встановив його електромагнітну природу. Тому електродинаміка є теоретичною базою оптики. З іншого боку, завдяки роботам Генріха Герца, який експериментально підтвердив існування електромагнітних хвиль і отримав хвилі радіочастотного діапазону, електромагнітні хвилі набули щонайширшого практичного застосування. Зокрема, вони є незамінним засобом передачі інформації у сучасних системах зв’язку.

Загальні властивості електромагнітних хвиль

Хвильові рівняння електромагнітного поля. Вектори електромагнітного поля Е  і  Н задовольняють окремим диференціальним рівнянням, які можна одержати з рівнянь Максвелла. Для діелектричного середовища за відсутності сторонніх зарядів і струмів вони мають вигляд:

		(22.42)
		(22.43)

де    відповідно, електрична й магнітна сталі,    діелектрична та магнітна проникності середовища. Рівняння (22.42) і (22.43)  ідентичні до (22.14)  і  є  хвильовими рівняннями. Загальні розв’язки цих рівнянь у випадку полів, які змінюються з часом, являють собою рівняння електричної  Е(r, t) та магнітної  Н(r, t)  хвиль. Але нестаціонарні електричне та магнітне поля є органічно взаємопов’язаними, тому вказані рівняння не є незалежними і в сукупності складають рівняння єдиної електромагнітної хвилі. Теоретичне передбачення існування електромагнітних хвиль, яке стало одним із найбільших відкриттів Максвелла, пізніше експериментально підтверджено Герцом.

З хвильових рівнянь та безпосередньо з рівнянь Максвелла випливають такі загальні властивості електромагнітних хвиль.

Швидкість поширення електромагнітних хвиль. Порівняння (22.42), (22.43) із загальним рівнянням (22.14) показує, що швидкість електромагнітної хвилі в середовищі

(22.44)

У вакуумі (  ) ця швидкість дорівнює

(22.45)

Співпадіння швидкості електромагнітних хвиль у вакуумі зі швидкістю світла дозволило Максвеллу висловити думку про електромагнітну природу світла, вірогідність якої була доведена всім подальшим розвитком фізичної оптики.

Виходячи з (22.45), швидкість поширення електромагнітної хвилі у середовищі можна записати, як

(22.46)

Реально електромагнітні хвилі можуть існувати тільки в діелектриках, які є немагнітними середовищами (  ), отже практично

(22.47)

Поперечність електромагнітних хвиль. Коливання векторів  Е  та  Н  в електромагнітній хвилі відбуваються у напрямках, перпендикулярних до напрямку поширення хвилі, тобто, до напрямку хвильового вектора  k (або вектора швидкості хвилі v). Отже, електромагнітні хвилі є поперечними.  Електричне та магнітне поля хвилі теж є взаємно перпендикулярними й завжди напрямлені так, що вектори Е, Н, k  утворюють праву трійку (рис. 22.9), тобто, при обертанні правого гвинта від першого вектора до другого він буде угвинчуватись у напрямку третього вектора^[1]

 

Зв’язок між величиною полів. Не лише напрямки, а й миттєві значення модулів векторів електричного та магнітного поля в електромагнітній хвилі жорстко пов’язані між собою співвідношенням

(22.48)

Якщо хвиля поширюється за відсутності в просторі будь-яких перепон, дане співвідношення виконується й для проекцій векторів на осі, вздовж яких відбуваються їх коливання. Це означає, що коливання електричного та магнітного полів у вільній електромагнітній хвилі є синфазними. Тому плоска монохроматична електромагнітна хвиля описується загальними рівняннями

.

(22.49)

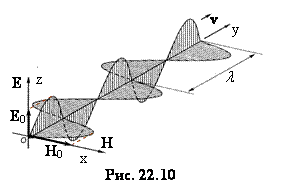
Якщо хвиля поширюється вздовж однієї з координатних осей, наприклад, OY, розподіл полів уздовж напрямку поширення виглядає, як показано на рис. 22.10.

Доведення властивостей електромагнітних хвиль^[2]. Запишемо систему рівнянь Максвелла (19.14), (19.15) для безмежного однорідного ізотропного діелектричного середовища, в якому відсутні сторонні заряди (  ) і струми (  ), де  і :

		(22.50а)
		(22.50б)
		(22.50в)
		(22.50г)

Аби отримати диференціальні рівняння для кожного з полів окремо, треба в правих частинах (22.50б,г) позбавитися “чужих” полів − Н або Е, відповідно. Це можна зробити, взявши ротор від одного з рівнянь, наприклад (22.50б), і зробивши потрібну підстановку з (22.50г). Справді,

.

(22.51)

Тут ураховано, що координати й час є незалежними змінними, і диференціювання по них можна проводити в будь-якій послідовності. Тепер візьмемо до уваги, що ротор ротора можна розглядати як символічний подвійний векторний добуток і скористаємося відомою тотожністю

Тоді, врахувавши, що, згідно з (22.50а), , отримаємо:

.

Нарешті, підставивши в (22.51), отриманий вираз подвійного ротора  Е, а також вираз ротора  Н із (22.50г), отримуємо хвильове рівняння (22.42). Такі самі перетворення в (22.50г) приводять до хвильового рівняння (22.43).

Доведемо, що електромагнітна хвиля є поперечною. Для цього визначимо дивергенцію поля Е

у плоскій монохроматичній хвилі. Із (22.49) для проекції електричного вектора на вісь ОХ маємо:

Аналогічно визначаються й дві інші проекції дві інші проекції, тому

або згорнуто

Звідси, відповідно до (22.50а), маємо

Отже, вектор  Е  є перпендикулярним до хвильового вектора, тобто, до напрямку поширення хвилі. Так само доводиться аналогічне співвідношення  для магнітного вектора.

Визначимо тепер взаємну орієнтацію векторів  Е  і  Н у хвилі, скориставшись рівнянням (22.50б). Нехай хвиля (22.49) поширюється у напрямку осі OY і коливання електричного поля відбуваються вздовж осі ОZ, отже  k =е_yk  і Е = е_zЕ_z.  У такому разі

Оскільки величина  Е  залежить тільки від координати y, то  , і

(22.52)

Визначимо тепер праву частину в рівнянні (22.50б). Про напрям магнітного вектора нам нічого невідомо, крім того, що він перпендикулярний до осі OY. Тому подамо його у вигляді . Відтак похідна по часу записується як

Підставивиши цей вираз та вираз (22.52) у рівняння (22.50б), формально дістанемо:

(22.53)

Але ця рівність є можливою тільки за умови , звідки випливає, що Н_z = 0  і  Н = е_хН_х. Оскільки при цьому  Е = е_zЕ_z і  k =е_yk, доходимо висновку, що вектори  Е  і  Н  у  хвилі є взаємно перпендикулярними й утворюють із вектором  k  праву трійку, як показано на рис. 22.9.

                Знайдемо тепер співвідношення між величиною полів у хвилі. Для хвилі з розглянутими напрямками векторів із (22.49) . Підставивши цей вираз у (22.53), урахувавши, що  Н_z = 0, отримаємо:

=

Звідси для коливань магнітного поля в якійсь фіксованій точці y = y₀ маємо:

Інтегрування цього рівняння дає:

Отримане співвідношення виконується при будь-яких значеннях y₀, отже коливання полів у монохроматичній хвилі є синфазними, як це відображено в рівняннях (22.49). При цьому

де враховано, що  − фазова швидкість хвилі. Звідси після підстановки виразу    (22.44) дістанемо:

 

^[1] Це правило зберігається й при циклічній зміні послідовності векторів: Н, k, Е та k, Е, Н.

^[2] Цей пункт є не обов’язковим для детального вивчення.