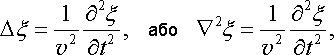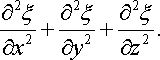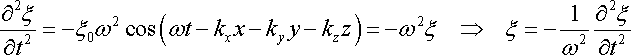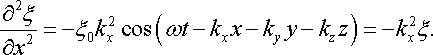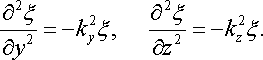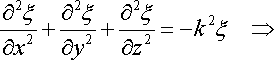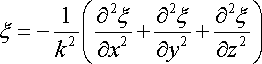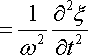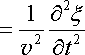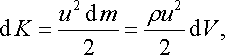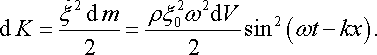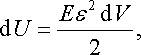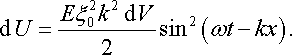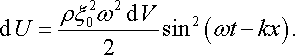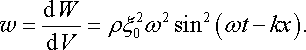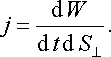37. Хвильове рівняння

Рівняння будь-якої хвилі можна одержати як розв’язок єдиного диференціального рівняння, що називається хвильовим рівнянням. Для незагасаючих хвиль воно має вигляд

(22.14)

де символи    або  означають оператор Лапласа. У декартових координатах

=

Що це дійсно так, проілюструємо на прикладі плоскої монохроматичної хвилі.

Знайдемо другі частинні похідні по часу і по координатах від функції    в рівнянні (22.12,а):

Аналогічно:

Додавши похідні по всіх координатах, одержимо

,

де враховано, що . Прирівнявши вирази  через похідні і, врахувавши (22.7), знаходимо:

 

38. Енергія та інтенсивність механічної хвилі Механічні хвилі

Механічні хвилі можуть існувати тільки у середовищах, які мають пружні властивості. В таких середовищах, завдяки наявності сил взаємодії між окремими частинками, рух однієї з них викликає рух інших. Тому збурення все далі віддаляється від місця його виникнення, тобто утворюється хвиля.

Енергія та інтенсивність механічної хвилі

У пружному середовищі, в якому поширюється механічна хвиля, зосереджена енергія хвилі, що складається з кінетичної енергії  К  коливального руху частинок та потенціальної енергії U  пружної деформації середовища, створюваної цим рухом. Розподіл енергії у кожній точці простору визначається об’ємною густиною  .  Для її визначення знайдемо вираз  dW = dK + dU  енергії, що зосереджена в елементарному об’ємі  dV, у межах якого зміщення та швидкості руху всіх точок можна вважати однаковими. Якщо на момент t  швидкість коливального руху точок виділеного об’єму дорівнює u, то його кінетична енергія

де    густина середовища. Для плоскої монохроматичної хвилі швидкість u  визначається рівнянням (22.15), отже

Тепер знайдемо  dU.  З механіки відомо, що потенціальна енергія пружної деформації в об’ємі  dV  визначається, як

де  Е  модуль пружності (модуль Юнга),     відносна деформація. Для її визначення уявімо стержень із перерізом S, по якому поширюється поздовжня хвиля. Виділимо в стержні елементарний шар об’єму  dV = Sdx  (рис. 22.4а). Унаслідок зміщення частинок товщина шару  dx  за час  dt  зміниться на величину    (рис. 22.4б), отже відносна деформація дорівнюватиме

З рівняння хвилі (22.2) маємо:

отже

Виразивши модуль Юнга з формули (22.17) та урахувавши, що , одержимо

Відтак повна енергія  dW  у виділеному об’ємі  dV

(22.20)

а об’ємна густина енергії пружної хвилі

(22.20а)

Із виразів (22.20) і (22.20а) випливає, що енергія хвилі в будь-який заданий момент часу нерівномірно розподілена в просторі, і в будь-якій точці змінюється з часом. При цьому координата довільної точки із заданим значенням    задовольняє рівнянню

Це означає, що в монохроматичній хвилі енергія переноситься від джерела до віддалених точок, і швидкість перенесення дорівнює фазовій швидкості хвилі^[1]. Мірою перенесення енергії хвилі є густина потоку енергії  j − енергія, що переноситься за одиницю часу крізь одиничну площадку, перпендикулярну до напрямку поширення хвилі:

(22.21)

За час  dt  крізь площадку    хвиля переносить енергію, зосереджену в об’ємі    і рівну  .  Отже, величина густини потоку енергії  j  дорівнює

(22.22)

Оскільки напрям перенесення енергії співпадає з напрямом вектора v, то густину потоку енергії розглядають як вектор

(22.23)

який називають вектором Умова. Розгорнуто він записується, як

(22.24)

 

Частота хвиль переважно є досить високою,  і  величина  j  швидко змінюється з часом. Тому для практики являє інтерес середнє у часі значення модуля вектора, вектора густини потоку енергії, яке називається інтенсивністю хвилі  І:

Середнє значення функції sin² легко знайти, скориставшись тотожністю  :

Оскільки для кожного додатного значення функції косинус на протязі періоду обов’язково існує таке саме по модулю від’ємне значення, то ^[2], отже  Таким чином

(22.25)

Вартий уваги той факт, що інтенсивність хвилі є пропорційною квадратові  її  амплітуди:

(22.25а)

^[1] У реальних хвилях енергія переноситься із груповою швидкістю.

^[2] Корисно взяти до уваги, що цей результат є чинним і для будь-якої іншої періодичної знакозмінної функції, графік якої є симетричним відносно осі абсцис.