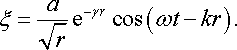- •36. Хвилі
- •Загальні характеристики хвиль
- •Поздовжні та поперечні хвилі. Монохроматичні хвилі
- •Рівняння плоскої монохроматичної хвилі
- •Характеристики монохроматичної хвилі
- •Фаза хвилі. Фазова швидкість і хвильові поверхні
- •Рівняння сферичної та циліндричної хвиль
- •Різниця фаз та різниця ходу хвиль
- •Рівняння плоскої хвилі, що поширюється у довільному напрямі
- •Загасаючі хвилі
- •37. Хвильове рівняння
- •38. Енергія та інтенсивність механічної хвилі Механічні хвилі
- •Енергія та інтенсивність механічної хвилі
- •Швидкість механічних хвиль
- •39. Хвильові пакети. Групова швидкість
- •40. Стоячі хвилі
- •41. Хвильове рівняння для електромагнітної хвилі. Доведення поперечності електромагнітної хвилі. Електромагнітні хвилі
- •Загальні властивості електромагнітних хвиль
- •42. Вектор Пойнтінга та інтенсивність електромагнітної хвилі
- •Шкала електромагнітних випромінювань
Різниця фаз та різниця ходу хвиль
При
розгляді різних хвильових явищ важливу
роль відіграє різниця фаз
![]()
![]() однієї
хвилі
у двох різних точках, або двох різних
хвиль у заданій точці в один і той самий
момент часу. Для однієї плоскої хвилі
з виразу (22.6)
маємо
однієї
хвилі
у двох різних точках, або двох різних
хвиль у заданій точці в один і той самий
момент часу. Для однієї плоскої хвилі
з виразу (22.6)
маємо
|
|
(22.10) |
![]()
![]() різниця
відстаней від даних точок до джерела,
або, інакше, − відстань між точками,
відрахована вздовж променя. У випадку
сферичної та циліндричної хвилі
різниця
відстаней від даних точок до джерела,
або, інакше, − відстань між точками,
відрахована вздовж променя. У випадку
сферичної та циліндричної хвилі
|
|
(22.10а) |
Ці
ж формули стосуються й хвиль однакової
частоти та довжини хвилі, що приходять
у дану точку від двох джерел. При цьому
різницю відстаней від джерел до даної
точки
або
![]()
![]() називають
різницею ходу хвиль (або променів).
називають
різницею ходу хвиль (або променів).
Рівняння плоскої хвилі, що поширюється у довільному напрямі
Рівняння (22.2) стосується випадку поширення хвилі вздовж осі OX. Знайдемо тепер форму запису рівняння плоскої монохроматичної хвилі, що поширюється в довільному напрямі. Нехай, для спрощення, цей напрям є перпендикулярним до осі ОZ. Тоді вектор швидкості хвилі v лежить у площині XOY, а хвильові поверхні утворюють систему площин, перпендикулярних до v. Виберемо довільну точку D, положення якої задається радіусом-вектором r, проведемо через неї пряму АВ, яка зображує відповідну хвильову поверхню, рис. 22.3. Коливання всіх точок цієї хвильової поверхні є синфазними і співпадають із коливаннями точки С. Отже рівняння коливань точки D має вигляд
|
|
|
|
|
|
Відстань l виразимо через радіус-вектор r точки D та одиничний вектор (орт) нормалі n до хвильової поверхні, який задає напрям поширення хвилі:
|
|
|
Тоді маємо
|
|
|
Величина
|
|
(22.11) |
називається хвильовим вектором. Його модуль дорівнює хвильовому числу, а напрям збігається з напрямом поширення хвилі в даній точці простору. Відтак рівняння плоскої монохроматичної хвилі, що поширюється в довільному напрямі, записується як:
|
|
(22.12) |
У декартовій системі координат
|
|
(22.12а) |
Очевидно, що розглянуте раніше рівняння (22.2) є окремим випадком загального рівняння (22.12а), коли ky = kz = 0, і kх = k.
Загасаючі хвилі
Усе
розглянуте вище стосувалося випадку,
коли втрати енергії коливань при
поширенні хвилі відсутні. Якщо ж
середовище поглинає енергію хвилі, то
із збільшенням відстані від джерела
амплітуда коливань поступово зменшується
спостерігається
загасання хвилі. Дослід показує, що
загасання відбувається за експоненціальним
законом
![]()
![]() .
То ж рівняння плоскої, сферичної та
циліндричної хвиль, відповідно, вигляд
.
То ж рівняння плоскої, сферичної та
циліндричної хвиль, відповідно, вигляд
|
|
(22.13) |
|
|
(22.13а) |
|
|
(22.13б) |